Вопросы и задания для самоконтроля
Сформулировать определение понятия «плоская произвольная система сил».
Сформулировать теорему, выражающую метод Пуансо для произвольной системы сил.
Записать геометрическое условие равновесия произвольной системы сил.
Записать первую форму уравнений равновесия плоской произвольной системы сил.
Записать вторую форму уравнений равновесия плоской произвольной системы сил.
Записать третью форму уравнений равновесия плоской произвольной системы сил.
Записать векторную формулу для определения главного вектора сил.
Записать формулу для определения модуля главного вектора сил в декартовой системе отсчета.
Записать векторную формулу для определения главного момента системы сил относительно центра приведения.
1.20. Расчет фермы
Фермой называется геометрически неизменяемая шарнирно-стержневая конструкция. При этом все стержни фермы прямолинейные. Если оси всех стержней фермы лежат в одной плоскости, то ее называют плоской фермой. Точки, в которых сходятся оси стержней, называют узлами фермы, а те узлы, которыми ферма опирается на основания, называют опорными узлами. Стержни плоской фермы, расположенные по верхнему контуру, образуют верхний пояс, а расположенные по нижнему контуру – нижний пояс фермы. Вертикальные стержни называют стойками, а наклонные раскосами.
Н
Рис. 1.51
Совокупность стержней 2, 6, 10, 14 образует верхний пояс фермы, а совокупность стержней 4, 8, 12, 16 образует нижний пояс фермы.
В теоретической механике рассматривают идеализированные фермы, при расчете которых приняты следующие допущения:
Все внешние нагрузки к ферме прикладываются только в узлах.
Все шарниры считаются идеальными, т. е. трение в узлах фермы не учитывается.
Все стержни невесомые, т. е. они загружены только по концам.
Все силы, действующие на ферму, лежат в одной плоскости.
На каждый из стержней фермы действуют две силы, приложенные к его концам, которые при равновесии могут быть направлены только вдоль стержня. Следовательно, можно считать, что стержни фермы работают только на растяжение или сжатие.
В реальных фермах может и не быть шарниров, а при жестком соединении сваркой или заклепками стержни могут воспринимать и другие виды нагрузок (изгиб, кручение и т. д.). Однако результаты вычислений при принятых допущениях вполне пригодны для практики, причем расчет усилий в стержнях существенно облегчается.
1.21. Методология расчета усилий
В СТЕРЖНЯХ ПЛОСКОЙ ФЕРМЫ
Методологию расчета усилий в стержнях плоской фермы покажем на примере выполнения курсового задания С 2, которое входит в контрольную работу обучающихся.
1.21.1. Варианты курсового задания С 2
«Определение реакций опор и сил
в стержнях плоской фермы»
В курсовом задании С 2 требуется определить реакции опор фермы в зависимости от заданных сил Р1, Р2, а также усилия Si в стержнях. Варианты расчетных схем и нагрузки, действующие на фермы, приведены в табл. 1.2.
Таблица 1.2
|
Номер варианта |
Расчетная схема |
Исходные данные |
Определяемые величины |
Реакции, определяемые по методу Риттера |
|
1 |
2 |
3 |
4 |
5 |
|
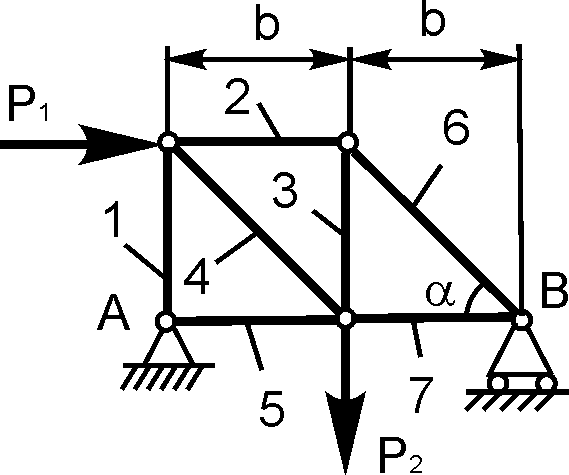
1 |
|
P1 =4 кН; Р2 =9 кН; = 300; b = 2 м
|
XA; YA; RB; S1 – S7 |
S4; S5; S6
|
|
2 |
|
P1 =2 кН; Р2=12 кН; = 600; b = 2 м
|
XВ; YВ; RА; S1 – S6 |
S1; S4; S6
|
|
3 |
|
P1 =10 кН; Р2 =10 кН; = 600; b = 2 м
|
XA; YA; RB; S1 – S5 |
S2; S3; S4
|
Продолжение табл. 1.2
|
1 |
2 |
3 |
4 |
5 |
|
4 |
|
P1 =2 кН; Р2 =12 кН; = 450; b = 2 м
|
XA; YA; RB; S1 – S8 |
S3; S4; S5
|
|
5 |
|
P1 =2 кН; Р2 =4 кН; = 600; b = 2 м
|
XВ; YВ; RА; S1 – S7 |
S4; S5; S6
|
|
6 |
|
P1 =3 кН; Р2 =7 кН; = 450; b = 2 м
|
XA; YA; RB; S1 – S7 |
S4; S5; S7
|
|
7 |
|
P1 =4 кН; Р2 =6 кН; = 600; b = 2 м
|
XВ; YВ; RА; S1 – S7 |
S4; S5; S6
|
Продолжение табл. 1.2
|
1 |
2 |
3 |
4 |
5 |
|
8 |
|
P1 =5 кН; Р2 =7 кН; = 450; b = 2 м
|
XВ; YВ; RА; S1 – S7 |
S4; S5; S6
|
|
9 |
|
P1 =10 кН; Р2 =8 кН; = 600; b = 2 м
|
XВ; YВ; RА; S1 – S9 |
S4; S5; S6
|
|
10 |
|
P1 =3 кН; Р2 =4 кН; = 450; b = 2 м
|
XA; YA; RB; S1 – S7 |
S1; S5; S6
|
|
11 |
|
P1 =2 кН; Р2 =6 кН; = 450; b = 2 м
|
XA; YA; RB; S1 – S7 |
S2; S3; S7
|
Продолжение табл. 1.2
|
1 |
2 |
3 |
4 |
5 |
|
12 |
|
P1 =5 кН; Р2 =7 кН; = 450; b = 2 м
|
XВ; YВ; RА; S1 – S7 |
S4; S5; S6
|
|
13
|
α
|
P1 =4 кН; Р2 =6 кН; = 450; b = 2 м
|
XA; YA; RB; S1 – S7 |
S4; S5; S6
|
|
14 |
|
P1 =3 кН; Р2 =5 кН; = 300; b = 2 м
|
XA; YA; RB; S1 – S7 |
S4; S5; S6
|
|
15 |
|
P1 =2 кН; Р2 =2 кН; = 600; b = 2 м
|
XA; YA; RB; S1 – S7 |
S4; S5; S6
|
Продолжение табл. 1.2
|
1 |
2 |
3 |
4 |
5 |
|
16 |
|
P1 =5 кН; Р2 =6 кН; = 600; b = 2 м
|
XA; YA; RB; S1 – S5 |
S2; S3; S4
|
|
17 |
|
P1 =4 кН; Р2 =4 кН; = 300; b = 2 м
|
XA; YA; RB; S1 – S7 |
S4; S5; S6
|
|
18 |
|
P1 =5 кН; Р2 =2 кН; = 600; b = 2 м
|
XВ; YВ; RА; S1 – S7 |
S2; S3; S4
|
|
19 |
|
P1 =5 кН; Р2 =7 кН; = 450; b = 2 м
|
XВ; YВ; RА; S1 – S7 |
S4; S5; S6
|
Продолжение табл. 1.2
|
1 |
2 |
3 |
4 |
5 |
|
20 |
|
P1 =2 кН; Р2 =3 кН; = 300; b = 2 м
|
XA; YA; RB; S1 – S5 |
S2; S3; S4
|
|
21 |
|
P1 =3 кН; Р2 =2 кН; = 450; b = 2 м
|
XВ; YВ; RА; S1 – S7 |
S4; S5; S6
|
|
22 |
|
P1 =2 кН; Р2 =4 кН; = 450; b = 2 м
|
XA; YA; RB; S1 – S9 |
S2; S3; S7
|
|
23 |
|
P1 =5 кН; Р2 =8 кН; = 300; b = 2 м
|
XA; YA; RB; S1 – S7 |
S2; S3; S4
|
Продолжение табл. 1.2
|
1 |
2 |
3 |
4 |
5 |
|
24 |
|
P1 =6 кН; Р2 =10 кН; = 450; b = 2 м
|
XA; YA; RB; S1 – S7 |
S4; S5; S6
|
|
25 |
|
P1 =7 кН; Р2 =10 кН; = 450; b = 2 м
|
XВ; YВ; RА; S1 – S7 |
S4; S5; S6
|
|
26 |
|
P1 =8 кН; Р2 =12 кН; = 300; b = 2 м
|
XA; YA; RB; S1 – S7 |
S4; S5; S6
|
|
27 |
|
P1 =9 кН; Р2 =14 кН; = 450; b = 2 м
|
XA; YA; RB; S1 – S7 |
S4; S6; S7
|
Окончание табл. 1.2
|
1 |
2 |
3 |
4 |
5 |
|
28 |
|
P1 =10 кН; Р2 =5кН; = 300; b = 2 м
|
XA; YA; RB; S1 – S7 |
S2; S3; S4
|
|
29 |
|
P1 =12 кН; Р2 =8 кН; = 450; b = 2 м
|
XВ; YВ; RА; S1 – S7 |
S4; S5; S6
|
|
30 |
|
P1 =5 кН; Р2 =10 кН; = 450; b = 2 м
|
XA; YA; RB; S1 – S7 |
S4; S5; S6
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
α
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|