
Литература / Advanced Digital Signal Processing and Noise Reduction (Saeed V. Vaseghi) / 09 - Power spectrum and correlation
.pdfModel-Based Power Spectrum Estimation |
283 |
9.5.3 Moving-Average Power Spectrum Estimation
A moving-average model is also known as an all-zero or a finite impulse response (FIR) filter. A signal x(m), modelled as a moving-average process, is described as
Q |
|
|
x(m)= ∑bk e(m − k) |
(9.68) |
|
k = |
0 |
|
where e(m) is a zero-mean random input and Q is the model order. The cross-correlation of the input and output of a moving average process is given by
rxe (m) =E[x( j)e( j − m)] |
|
|
|
Q |
|
(9.69) |
|
=E ∑ bk e( j − k)e( j − m) =σ e2bm |
|||
|
|||
k=0 |
|
|
|
and the autocorrelation function of a moving average process is
|
|
|
Q−|m| |
|
|
|
σ |
2 |
∑ b b |
, |
| m |≤ Q |
r (m)= |
e |
k k +m |
|
(9.70) |
|
xx |
|
|
k=0 |
|
|
|
|
|
|
| m |>Q |
|
|
0, |
|
|
|
|
From Equation (9.70), the power spectrum obtained from the Fourier transform of the autocorrelation sequence is the same as the power spectrum of a moving average model of the signal. Hence the power spectrum of a moving-average process may be obtained directly from the Fourier transform of the autocorrelation function as
|
Q |
|
|
PMA = |
∑ r (m)e− j2 |
πfm |
(9.71) |
XX |
xx |
|
|
m=−Q
Note that the moving-average Blackman–Tukey method of autocorrelation sequence.
spectral estimation is identical to the estimating periodograms from the
284 |
Power Spectrum and Correlation |
9.5.4 Autoregressive Moving-Average Power Spectrum
Estimation
The ARMA, or pole–zero, model is described by Equation (9.47). The relationship between the ARMA parameters and the autocorrelation sequence can be obtained by multiplying both sides of Equation (9.47) by x(m–j) and taking the expectation:
P
rxx ( j) = − ∑ akrxx ( j − k ) +
k =1
Q |
|
∑ bkrxe ( j − k) |
(9.72) |
k= 0
The moving-average part of Equation (9.72) influences the autocorrelation values only up to the lag of Q. Hence, for the autoregressive part of Equation (9.72), we have
P |
|
rxx (m) = − ∑ak rxx (m − k ) for m > Q |
(9.73) |
k=1
Hence Equation (9.73) can be used to obtain the coefficients ak, which may then be substituted in Equation (9.72) for solving the coefficients bk. Once the coefficients of an ARMA model are identified, the spectral estimate is given by
|
|
|
|
Q |
|
|
2 |
|
||
|
|
|
|
|
|
|||||
|
|
|
|
∑bk e |
− j2πfk |
|
|
|
|
|
P ARMA |
( f ) = σ 2 |
|
k=0 |
|
|
|
|
|
(9.74) |
|
|
|
|
|
|
|
|||||
XX |
e |
|
|
P |
|
|
2 |
|||
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1+∑ak e− j2πfk |
|
|
|
||||
|
|
|
|
k =1 |
|
|
|
|
|
|
where σe2 is the variance of the input of the ARMA model. In general, the poles model the resonances of the signal spectrum, whereas the zeros model the anti-resonances of the spectrum.
9.6High-Resolution Spectral Estimation Based on Subspace Eigen-Analysis
The eigen-based methods considered in this section are primarily used for estimation of the parameters of sinusoidal signals observed in an additive white noise. Eigen-analysis is used for partitioning the eigenvectors and the

High-Resolution Spectral Estimation |
285 |
eigenvalues of the autocorrelation matrix of a noisy signal into two subspaces:
(a)the signal subspace composed of the principle eigenvectors associated with the largest eigenvalues;
(b)the noise subspace represented by the smallest eigenvalues.
The decomposition of a noisy signal into a signal subspace and a noise subspace forms the basis of the eigen-analysis methods considered in this section.
9.6.1 Pisarenko Harmonic Decomposition
A real-valued sine wave can be modelled by a second-order autoregressive (AR) model, with its poles on the unit circle at the angular frequency of the sinusoid as shown in Figure 9.5. The AR model for a sinusoid of frequency Fi at a sampling rate of Fs is given by
x(m)= 2cos(2πFi / Fs ) x(m −1)−x(m − 2)+Aδ (m − t0 ) |
(9.75) |
where Aδ(m–t0) is the initial impulse for a sine wave of amplitude A. In general, a signal composed of P real sinusoids can be modelled by an AR model of order 2P as
2P
x(m) = ∑ak x(m − k)+Aδ (m − t0 )
k=1
 X( f )
X( f )
 ω0
ω0 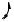 −ω0
−ω0
(9.76)
Pole
F0 f
Figure 9.5 A second order all pole model of a sinusoidal signal.
286 |
Power Spectrum and Correlation |
The transfer function of the AR model is given by
H (z) = |
A |
|
2P |
|
|
|
|
|
|
1− ∑ak z |
−k |
|
k=1 |
|
= |
|
|
A |
|
|
|
|
(9.77) |
|
P |
|
|
||
|
∏(1− e |
− j2πFk z |
−1)(1− e+ j2πFk z−1) |
|
|
k=1 |
|
|
|
where the angular positions of the poles on the unit circle, e± j2πFk , correspond to the angular frequencies of the sinusoids. For P real sinusoids observed in an additive white noise, we can write
y(m) = x(m) + n(m)
2P
= ∑ak x(m − k) + n(m)
k =1
Substituting [y(m–k)–n(m–k)] for x(m–k) in Equation (9.73) yields
2P |
2P |
y(m) − ∑ak y(m − k)= n(m)− ∑ak n(m − k) |
|
k =1 |
k =1 |
(9.78)
(9.79)
From Equation (9.79), the noisy sinusoidal signal y(m) can be modelled by an ARMA process in which the AR and the MA sections are identical, and the input is the noise process. Equation (9.79) can also be expressed in a vector notation as
yTa = nTa |
(9.80) |
where yT=[y(m), . . ., y(m–2P)], aT=[1, a1, . . ., a2P] and nT=[n(m), . . ., n(m–2P)]. To obtain the parameter vector a, we multiply both sides of Equation (9.80) by the vector y and take the expectation:
E[ yyT ] a=E[ ynT ]a |
(9.81) |
or |
|
Ryy a = Ryn a |
(9.82) |
where E[ yyT ]= Ryy , and E[ ynT ]= Ryn can be written as
High-Resolution Spectral Estimation |
287 |
Ryn =E[(x + n)nT ]
= E[nnT ]= Rnn =σ n2I (9.83)
where σn2 is the noise variance. Using Equation (9.83), Equation (9.82) becomes
Ryy a =σ n2 a |
(9.84) |
Equation (9.84) is in the form of an eigenequation. If the dimension of the matrix Ryy is greater than 2P × 2P then the largest 2P eigenvalues are associated with the eigenvectors of the noisy sinusoids and the minimum eigenvalue corresponds to the noise variance σn2 . The parameter vector a is obtained as the eigenvector of Ryy, with its first element unity and associated with the minimum eigenvalue. From the AR parameter vector a, we can obtain the frequencies of the sinusoids by first calculating the roots of the polynomial
1+ a z−1 |
+ a |
2 |
z−2 |
+ + a |
2 |
z−2P+2 |
+ a z−2P+1 |
+ z −2P = 0 |
(9.85) |
1 |
|
|
|
|
1 |
|
|
Note that for sinusoids, the AR parameters form a symmetric polynomial; that is ak=a2P–k. The frequencies Fk of the sinusoids can be obtained from the roots zk of Equation (9.85) using the relation
zk =e |
j2πFk |
(9.86) |
|
The powers of the sinusoids are calculated as follows. For P sinusoids observed in additive white noise, the autocorrelation function is given by
|
|
P |
|
|
|
|
r |
yy |
(k)=∑ P cos2kπF |
+σ 2 |
δ (k) |
(9.87) |
|
|
i |
i |
n |
|
|
|
i=1
where Pi = Ai2 / 2 is the power of the sinusoid Ai sin(2πFi), and white noise affects only the correlation at lag zero ryy(0). Hence Equation (9.87) for the correlation lags k=1, . . ., P can be written as
288 |
|
|
|
|
cos2πF |
cos2πF |
|
|
1 |
2 |
|
cos4πF1 |
cos4πF2 |
||
|
|
|
|
|
|||
|
|
||
|
|
cos2PπF2 |
|
cos2PπF1 |
|||
Power Spectrum and Correlation
cos2πF P |
r (1) |
1
cos4πFP P2 = ryy (2)
cos2P FP PP ryy (P)P yy
(9.88)
Given an estimate of the frequencies Fi from Equations (9.85) and (86), and an estimate of the autocorrelation function rˆyy (k) , Equation (9.88) can be solved to obtain the powers of the sinusoids Pi. The noise variance can then be obtained from Equation (9.87) as
|
|
|
P |
|
σ 2 |
= r |
yy |
(0) − ∑P |
(9.89) |
n |
|
i |
|
i=1
9.6.2Multiple Signal Classification (MUSIC) Spectral Estimation
The MUSIC algorithm is an eigen-based subspace decomposition method for estimation of the frequencies of complex sinusoids observed in additive white noise. Consider a signal y(m) modelled as
P |
|
|
y(m)=∑ A e |
− j(2πFk m+φk ) +n(m) |
(9.90) |
k |
|
|
k=1 |
|
|
An N-sample vector y=[y(m), . . ., y(m+N–1)] of the noisy signal can be written as
y = x + n
= Sa + n |
(9.91) |
|
|
where the signal vector x=Sa is defined as |
|
|
x(m) |
|
|
e |
j2πF1m |
|
x m + |
|
|
|
|||
j2πF1(m+1) |
||||||
|
||||||
|
( 1) |
|
= |
e |
|
|
|
|
|
|
|
||
|
|
|
|
|||
|
|
|||||
|
|
|
|
j2πF1(m+N −1) |
||
x(m + N − |
1) |
e |
|
|
||
e j2πF2m e j2πF2 (m+1)
e j2πF2 (m+N −1)
|
|
e j2πFPm |
|
A e j2πφ1 |
|
|
|
|
|
|
1 |
|
|
e j2πFP (m+1) |
A e j2πφ2 |
|
||||
|
|
|
|
2 |
|
|
|
|
|
|
|
||
|
|
|
|
|||
|
e |
j2πFP (m+N −1) |
|
APe |
j2πφP |
|
|
|
|
|
|||
(9.92)
High-Resolution Spectral Estimation |
289 |
The matrix S and the vector a are defined on the right-hand side of Equation (9.92). The autocorrelation matrix of the noisy signal y can be written as the sum of the autocorrelation matrices of the signal x and the noise as
Ryy = Rxx + Rnn
(9.93)
= SPS H +σ2nI
where Rxx=SPSH and Rnn=σn2I are the autocorrelation matrices of the signal and noise processes, the exponent H denotes the Hermitian transpose, and the diagonal matrix P defines the power of the sinusoids as
|
|
|
P = aa H = diag[P ,P |
, ,P |
] |
(9.94) |
|||||
|
|
|
|
|
1 |
|
2 |
P |
|
|
|
where |
P |
= A2 |
is the power of |
the |
complex sinusoid |
e− j2πFi . The |
|||||
|
i |
i |
|
|
|
|
|
|
|
|
|
correlation matrix of the signal can also be expressed in the form |
|||||||||||
|
|
|
|
|
P |
|
|
|
|
|
|
|
|
|
R |
xx |
=∑ P s |
k |
sH |
|
(9.95) |
||
|
|
|
|
k |
|
|
k |
|
|
||
|
|
|
|
|
k=1 |
|
|
|
|
|
|
where skH =[1,e j2πFk , ,e j2π(N −1)Fk ]. Now consider an eigen-decomposition of the N × N correlation matrix Rxx
N |
|
Rxx = ∑λk vk vkH |
|
k =1 |
(9.96) |
P |
|
= ∑ |
λk vk vkH |
k =1 |
|
where λk and vk are the eigenvalues and eigenvectors of the matrix Rxx respectively. We have also used the fact that the autocorrelation matrix Rxx of P complex sinusoids has only P non-zero eigenvalues, λP+1=λP+2, ..., λN=0. Since the sum of the cross-products of the eigenvectors forms an identity matrix we can also express the diagonal autocorrelation matrix of the noise in terms of the eigenvectors of Rxx as

290 |
Power Spectrum and Correlation |
|
|
N |
|
|
Rnn =σ n2I=σ n2 ∑vk vkH |
(9.97) |
k=1
The correlation matrix of the noisy signal may be expressed in terms of its eigenvectors and the associated eigenvalues of the noisy signal as
P |
|
N |
|
Ryy =∑λk vk vkH + σn2 |
∑vk vkH |
|
|
k=1 |
k =1 |
(9.98) |
|
P |
|
N |
|
|
|
||
=∑ |
(λk + σn2 )vk vkH + σn2 ∑vk vkH |
|
|
k=1 |
|
k=P+1 |
|
From Equation (9.98), the eigenvectors and the eigenvalues of the correlation matrix of the noisy signal can be partitioned into two disjoint subsets (see Figure 9.6). The set of eigenvectors {v1, . . ., vP}, associated with the P largest eigenvalues span the signal subspace and are called the principal eigenvectors. The signal vectors si can be expressed as linear combinations of the principal eigenvectors. The second subset of eigenvectors {vP+1, . . ., vN} span the noise subspace and have σn2 as their eigenvalues. Since the signal and noise eigenvectors are orthogonal, it follows that the signal subspace and the noise subspace are orthogonal. Hence the sinusoidal signal vectors si which are in the signal subspace, are orthogonal to the noise subspace, and we have
Eigenvalues
λ1+ σn2
λ2+ σn2
λ3+σn2
λP+ σn2
... |
λP+1 |
=λP+2 =λP+3 |
= λN= σn2 |
|
|
|
... |
Principal eigenvalues |
Noise eigenvalues |
index |
|
||
|
|
Figure 9.6 Decomposition of the eigenvalues of a noisy signal into the principal eigenvalues and the noise eigenvalues.
High-Resolution Spectral Estimation |
|
|
|
|
|
|
291 |
||||
|
|
|
N −1 |
− j2πFim = |
|
|
|
|
|
|
|
H |
( f )vk |
= |
∑vk (m)e |
0 |
i |
= |
= |
P |
+ |
(9.99) |
|
si |
|
|
1, ,P k |
|
1, ,N |
|
|||||
m=0
Equation (9.99) implies that the frequencies of the P sinusoids can be obtained by solving for the zeros of the following polynomial function of the frequency variable f:
N |
|
|
|
|
||
∑ sH ( f )vk |
|
|
(9.100) |
|||
k=P+1 |
|
|
|
|
||
In the MUSIC algorithm, the power spectrum estimate is defined as |
|
|||||
N |
|
|
2 |
|
||
P ( f )= ∑ |
sH |
( f )v |
k |
(9.101) |
||
|
||||||
XX |
|
|
|
|
||
k=P+ |
1 |
|
|
|
|
|
where s(f) = [1, ej2πf, . . ., ej2π(N-1)f] is the complex sinusoidal vector, and {vP+1, . . . ,vN} are the eigenvectors in the noise subspace. From Equations (9.102) and (9.96) we have that
PXX ( f i ) = 0 , i = 1, . . ., P |
(9.102) |
Since PXX(f) has its zeros at the frequencies of the sinusoids, it follows that the reciprocal of PXX(f) has its poles at these frequencies. The MUSIC spectrum is defined as
PMUSIC ( f ) = |
1 |
|
|
= |
|
1 |
|
|
||
|
|
|
|
|
|
|
(9.103) |
|||
XX |
N |
|
|
|
2 sH |
( f )V ( f )V H |
||||
|
|
sH ( f )vk |
|
( f )s( f ) |
||||||
|
|
|
||||||||
|
∑ |
|
|
|
|
|
|
|
|
|
|
k =P+1 |
|
|
|
|
|
|
|
||
where V=[vP+1, . . . ,vN] is the matrix of eigenvectors of the noise subspace. PMUSIC(f) is sharply peaked at the frequencies of the sinusoidal components of the signal, and hence the frequencies of its peaks are taken as the MUSIC estimates.
292 |
Power Spectrum and Correlation |
9.6.3 Estimation of Signal Parameters via Rotational Invariance Techniques (ESPRIT)
The ESPIRIT algorithm is an eigen-decomposition approach for estimating the frequencies of a number of complex sinusoids observed in additive white noise. Consider a signal y(m) composed of P complex-valued sinusoids and additive white noise:
P |
− j(2πFk m+φk ) +n(m) |
|
y(m)=∑ A e |
(9.104) |
|
k |
|
|
k=1
The ESPIRIT algorithm exploits the deterministic relation between sinusoidal component of the signal vector y(m)=[y(m), . . ., y(m+N–1]T and that of the time-shifted vector y(m+1)=[y(m+1), . . ., y(m+N)]T. The signal component of the noisy vector y(m) may be expressed as
x(m)= S a |
(9.105) |
where S is the complex sinusoidal matrix and a is the vector containing the amplitude and phase of the sinusoids as in Equations (9.91) and (9.92). A
complex sinusoid e j2πFim can be time-shifted by one sample through
multiplication by a phase term e j2πFi . Hence the time-shifted sinusoidal signal vector x(m+1) may be obtained from x(m) by phase-shifting each complex sinusoidal component of x(m) as
x(m +1) = SΦ a |
(9.106) |
where Φ is a P × P phase matrix defined as |
|
Φ = diag[e j2πF1 ,e j2πF2 , ,e j2πFP ] |
(9.107) |
The diagonal elements of Φ are the relative phases between the adjacent samples of the sinusoids. The matrix Φ is a unitary matrix and is known as a rotation matrix since it relates the time-shifted vectors x(m) and x(m+1). The autocorrelation matrix of the noisy signal vector y(m) can be written as
Ry(m) y(m) = SPS H + σn2I |
(9.108) |
