Затем, используя явный вид переходной функции (32) , |
с |
помощью теоремы о вычетах находим импульсную |
|
характеристику. |
|
h(n) 1 n , |
n 0,1, (34) |
Формула (34) показывает, что полученная импульсная характеристика имеет бесконечное число отличных от нуля элементов, поэтому она является бесконечной импульсной характеристикой.
Таким образом, рассматриваемый рекурсивный фильтр
является БИХ – фильтром.
31
Исследуем этот фильтр на устойчивость. Из формулы (32) видно, что переходная функция H(z) имеет одну особую точку
.z1Эта особая1 точка не попадает внутрь единичного круга | z | < 1 комплексной плоскости. Эта точка находится на краю этого
круга |
как |
|
это |
|
видно из рисунка. |
|
|
||||
|
|
|
z1 |
|
1 |
|
|
|
|
|
Im(z) |
|
|
|
|
1 |
|
|
z1 |
|
1 |
1 |
Re(z) |
1
Отсюда по теореме 2 следует, что рассматриваемый |
БИХ |
- фильтр неустойчив. |
32 |
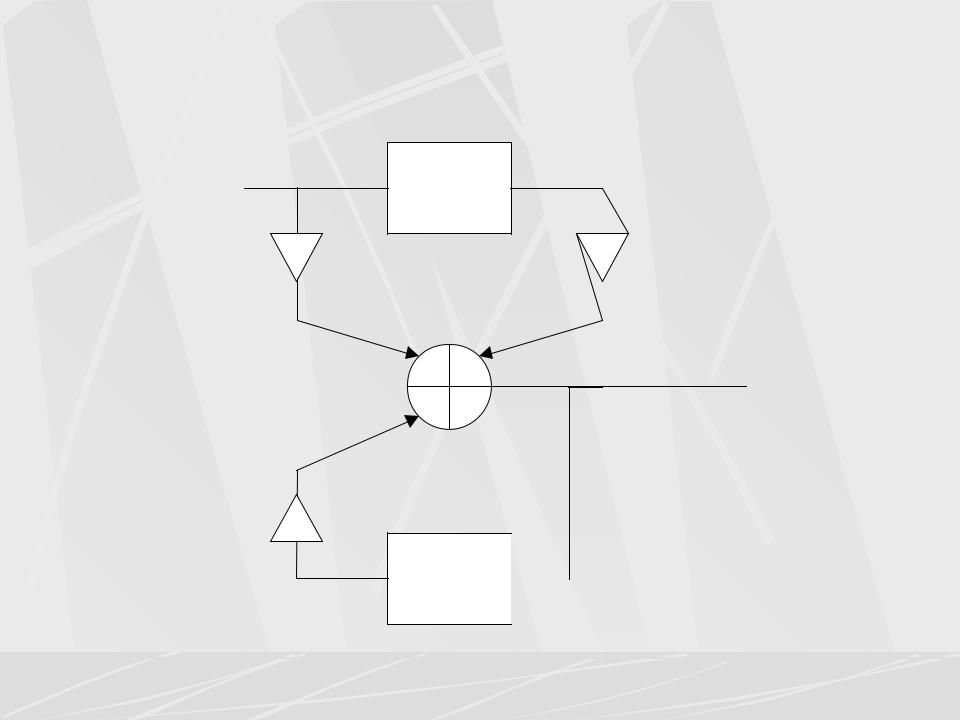
Пример 4. На рисунке показана структурная схема рекурсивного фильтра.
|
z 1 |
1 |
1 |
y(n)
1
z 1 
33
Написать основное разностное уравнение этого фильтра. Найти импульсную характеристику фильтра h(n), переходную функцию фильтра H(z) и частотную характеристику фильтра K( ). Из структурной схемы видно, что фильтр характеризуется следующими коэффициентами.
a1 1, |
b0 1, |
b1 1 |
(35) |
Подставляя коэффициенты (35) в общее разностное уравнение ЛДФ (17) получаем.
y(n) y(n 1) x(n) x(n 1) (36)
34
По общей формуле (31) для переходной функции, подставляя туда коэффициенты (35) находим переходную функцию рассматриваемого фильтра.
1 z 1 |
(37) |
H (z) 1 z 1 1 |
|
Переходная функция оказалась константой, равной единице.
Используя теорему вычетов, найдем импульсную характеристику. Сначала рассмотрим функцию f(z).
f (z) H (z) zn 1 zn 1, n 0,1, (38)
35
Выпишем несколько значений функции f(z) для некоторых n .
n 0, |
f (z) 1 |
, |
|
z |
|
n 1, |
f (z) 1, |
(39) |
n 2, |
f (z) z, |
|
n 3, |
f (z) z2 , |
|
|
|
|
Из соотношений (39) видно, что особая точка у функции f(z) будет только в одном случае, когда n = 0 . По общей теории вычетов это означает, что все элементы импульсной характеристики равны нулю кроме одного.
h(0) 0, |
h(n) 0, |
n 0 |
(40) |
36
Если n = 0 , то функция f(z) имеет полюс первого порядка в точке z1 0. Теперь используя теорему вычетов, находим h(z).
|
|
1 |
z |
|
|
|
h(n) выч f (z), 0 lim |
|
0 |
(41) |
|||
z 0 |
z |
|
|
|
||
lim 1 1
z 0
Мы видим что, рассматриваемый рекурсивный фильтр имеет частотную характеристику, у которой отличен от нуля только один элемент. Поэтому частотная характеристика является
конечной импульсной характеристикой.
Таким образом, рассматриваемый рекурсивный фильтр
является КИХ – фильтром.
37
Как мы показали выше, все КИХ – фильтры являются устойчивыми фильтрами. Значит, рассматриваемый рекурсивный фильтр является устойчивым фильтром.
Последнее, так как переходная функция оказалась равной единице, то и частотная характеристика фильтра будет равна единице.
K( ) 1 (42)
38
Суммарная информация о рекурсивных и нерекурсивных фильтрах.
Подведем промежуточный итог, касающийся свойств рекурсивных и нерекурсивных ЛДФ
Нерекурсивные фильтры
Конечная импульсная характеристика h(n)
КИХ – фильтры
Устойчивы всегда
39
Рекурсивные фильтры
Конечная импульсная |
|
Бесконечная импульсная |
характеристика |
|
характеристика |
КИХ – фильтры |
|
БИХ – фильтры |
Устойчивы всегда |
|
Устойчивы |
|
Неустойчивы |
40