Найдем импульсную характеристику h(n) нерекурсивного фильтра. Вспомним, что импульсную характеристику называют так же реакцией системы на единичный импульс. Это означает, что если на вход ЛДФ подать единичный импульс в виде символа Кронекера, то на выходе получился сигнал, совпадающий с импульсной характеристикой h(n).
Возьмем уравнение (19) нерекурсивного фильтра и поставим вместо входящего сигнала символ Кронекера.
x(n) n,0 (21)
В результате получим импульсную характеристику.
N |
N |
|
h(k) bn k n,0 |
bn k ,n bk (22) |
|
n 0 |
n 0 |
21 |
|
|
Таким образом, импульсная характеристика нерекурсивного фильтра находится очень просто, она равна коэффициентам bk основного разностного уравнения фильтра.
bn , |
n 0,1, , N |
(23) |
|
h(n) |
0, |
n N |
|
|
|
||
Формула (23) показывает, что полученная импульсная характеристика имеет конечное число отличных от нуля элементов, поэтому она является конечной импульсной характеристикой.
Значит все нерекурсивные фильтры являются КИХ – фильтрами.
22
Исследуем нерекурсивные фильтры на устойчивость. Для этого переходную функцию нерекурсивного фильтра (20) перепишем в следующем виде.
H (z) b0 |
|
b1 |
|
b2 |
|
bN |
(24) |
z |
z2 |
zN |
|
||||
|
|
|
|
|
Из формулы (24) мы видим, что у переходной функции имеется одна особая точка z = 0. Эта особая точка для членов суммы (24) является полюсом порядка m , где m - номер члена в сумме (24).
Например, для члена
bz22 ,
это будет полюс второго порядка m = 2 .
23
Для анализа устойчивости фильтра, важно, что эта особая точка лежит в комплексной плоскости в центре единичного круга | z | < 1. Отсюда по теореме 2 следует, что фильтр устойчив.
Значит все КИХ – фильтры являются устойчивыми
фильтрами.
Пример 2. Нерекурсивный фильтр описывается следующим разностным уравнением.
y(n) x(n 1) x(n 2) (25)
24
Найти импульсную характеристику фильтра h(n), переходную функцию фильтра H(z) и частотную характеристику фильтра K( ).
По формуле (23) находим импульсную характеристику.
h(0) 0, |
h(1) 1, |
h(2) 1, |
(26) |
h(n) 0, |
n 2 |
|
|
|
|
По формуле (24) находим переходную функцию.
1 |
|
1 |
|
z 1 |
|
|
H (z) z |
z2 |
z2 |
(27) |
|||
|
|
|
|
|
|
|
25
Далее делая в формуле (27) для переходной функции подстановку
z ei t
получаем частотную характеристику.
|
i t |
ei t 1 |
(28) |
|
K( ) H (e |
) ei 2 t |
|||
|
|
Если хотя бы один коэффициент отличен от нуля, то фильтр называется рекурсивным фильтром. Рекурсивный фильтр – это фильтр с обратными связями.
26
Пример 3. Рекурсивный фильтр описывается следующим разностным уравнением.
y(n) 2 y(n 1) y(n 2) x(n) x(n 1) (29)
Найти импульсную характеристику фильтра h(n), переходную функцию фильтра H(z) и частотную характеристику фильтра K( ). Этот фильтр характеризуется следующими коэффициентами.
a1 2, |
a2 1, |
b0 1, |
b1 1 (30) |
На рисунке показана структурная схема этого фильтра.
27
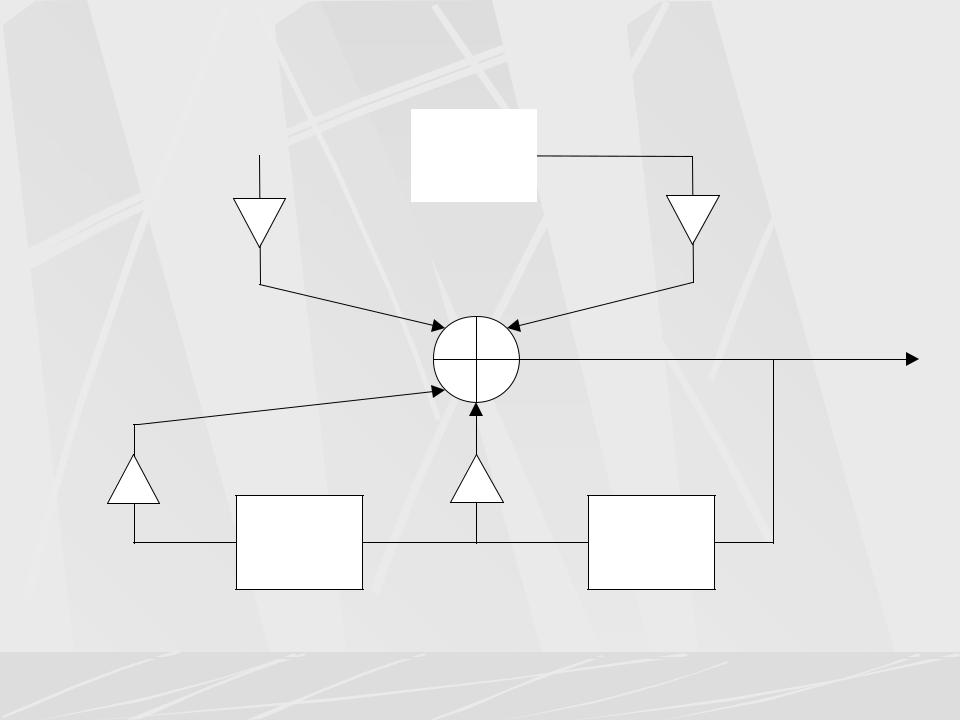
x(n) |
|
x(n 1) |
|
z 1 |
|||
|
1 |
||
1 |
|||
|
1 |
2 |
|
y(n 2) |
z 1 |
y(n 1) |
z 1 |
|
|
28
Этот фильтр был нами разобран на прошлой лекции. Поэтому воспользуемся полученными результатами.
Используя коэффициенты (30), по общей формуле для переходной функции
|
N |
|
|
bk z k |
|
H (z) |
k 0 |
(31) |
M |
||
1 am z m |
|
|
m 1
находим переходную функцию рассматриваемого фильтра.
29
H (z) |
1 z 1 |
|
z |
|
(32) |
|
1 2 z 1 z 2 |
z 1 |
|||||
|
|
|
||||
Далее делая в формуле (32) для переходной функции подстановку
z ei t
получаем частотную характеристику.
K( ) H (ei t ) |
ei t |
|
(33) |
|
ei t 1 |
||||
|
|
|||
30