Лекция 10
Свойства линейных дискретных фильтр
Устойчивость ЛДФ
Для анализа и синтеза фильтров важным является вопрос об их устойчивости. В лекции №8 мы рассмотрели этот вопрос. Напомним некоторые положения рассмотренные ранее.
Определение. Линейный дискретный фильтр называется устойчивым, если для любого ограниченного входящего сигнала x(n) C1 , выходящий сигнал также ограничен
y(n) C2 .
1
Там же было установлено, что устойчивость ЛДФ определяется условием, накладываемым на его импульсную характеристику. Была доказана следующая теорема.
Теорема 1. Необходимым и достаточным условием устойчивости ЛДФ, является выполнение условия.
h(k) C (1)
k 0
Здесь C - некоторая константа.
Теперь мы посмотрим на проблему устойчивости линейного фильтра с другой точки зрения. Для выяснения устойчивости ЛДФ мы обратимся к передаточной функции H(z).
2
Теорема 2. Для того чтобы ЛДФ был устойчив, необходимо и достаточно, чтобы все полюсы zn передаточной функции H(z) лежали в комплексной плоскости внутри единичного круга | z | < 1.
Теорему 2 примем без доказательства.
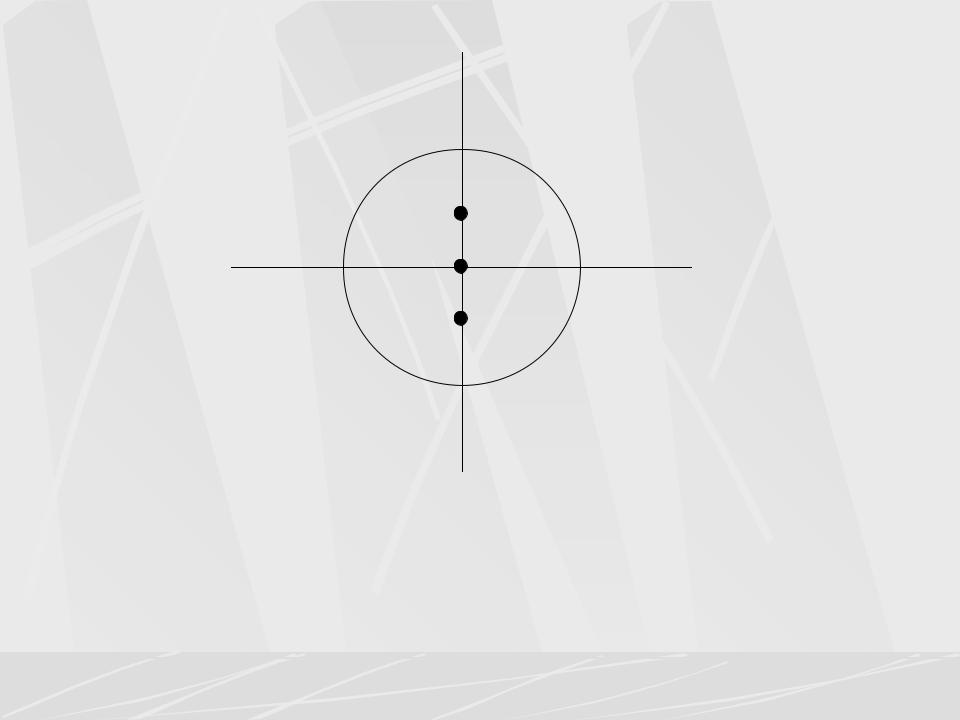
На следующих двух рисунках изображены полюсы передаточных функций двух ЛДФ.
3
|
Im(z) |
|
|
|
|
1 |
|
|
|
|
z3 |
|
|
|
1 |
z2 |
1 |
Re(z) |
|
z1 |
||||
|
|
|
1
На первом рисунке показаны полюсы передаточной функции H1(z) первого фильтра. Полюсов три и все они находятся внутри единичного круга | z | < 1. Поэтому первый фильтр устойчив.
4
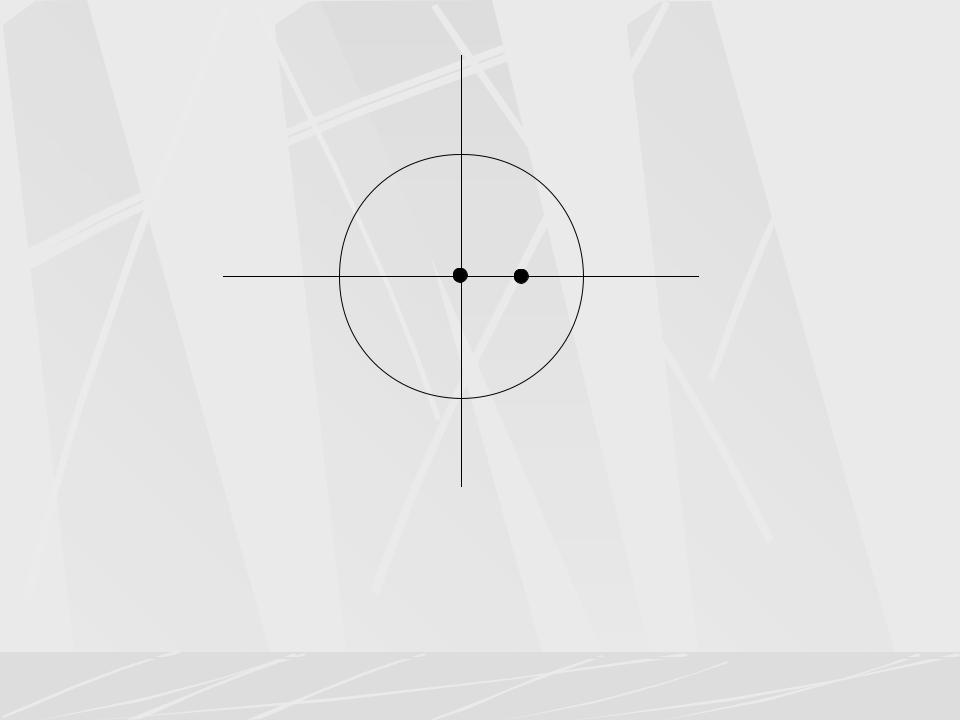
Im(z)
1
z3
1 |
z1 |
z2 |
1 |
Re(z) |
1
На втором рисунке показаны полюсы передаточной функции H2(z) второго фильтра. Полюсов тоже три, два из них z1, z2 лежат внутри единичного круга | z | < 1, а один полюс z3 вне единичного круга | z | 1. Значит, второй фильтр неустойчив. 5
Пример 1. На прошлой лекции мы рассматривали рекурсивный фильтр, который описывался следующим разностным уравнением.
y(n) a y(n 1) x(n) (2)
Надо выяснить, при каких значениях параметра a фильтр будет устойчив.
Мы нашли передаточную функцию это фильтра.
H (z) z z a
(3)
6
Единственная особая точка передаточной функции – это полюс первого порядка . Согласно теореме 2, фильтр будет устойчив, если особая точка будет лежать внутри единичного круга комплексной плоскости. Поэтому фильтр будет устойчив, если выполняется неравенство.
a 1 (4)
7
Частотная характеристика ЛДФ
Определение. Частотная характеристика линейного дискретного фильтра – это комплексная функция K( ) действительного переменного , и определяется соотношением.
K( ) H (ei t ) (5)
Здесь - это циклическая частота = 2 f, а t – шаг дискретизации. Таким образом, чтобы найти частотную характеристику фильтра, надо в переходной функции сделать замену.
z ei t |
(6) |
8
Вспомним, что передаточная функция H(z) является Z - образом импульсной характеристики h(n) фильтра.
H (z) h(n)
Поэтому передаточная функция и импульсная характеристика связаны друг с другом Z - преобразованием.
|
|
H (z) h(n) z n |
(7) |
n 0
Заменяя в сумме (7) комплексную переменную z с помощью замены (6), получаем формулу для нахождения частотной характеристики фильтра.
9
Поэтому частотную характеристику можно представить в виде ряда.
|
|
K( ) h(n) e i n t |
(8) |
n 0
Если частотную характеристику фильтра рассматривать, как функцию обычной частоты f , то ряд (8) примет вид.
|
|
K( f ) h(n) e i 2 f n t |
(9) |
n 0
10