- •Глава 6.Определенный интеграл и его приложения. Несобственные интегралы. §1. Задачи, приводящие к понятию определённого интеграла.
- •§2. Два определения интеграла Римана.
- •§3. Свойства сумм Дарбý.
- •§4. Теорема Дарбý. Эквивалентность двух определений интеграла Римана.
- •§5. Критерий интегрируемости. Интегрируемость непрерывных функций и монотонных функций.
- •§6. Свойства интегрируемых функций. Свойства определенного интеграла.
- •2˚. Свойства определенного интеграла.
- •4. Положительность интеграла.
- •5. Интегральная теорема о среднем значении.
- •§7. Интеграл с переменным верхним пределом. Связь определённого и неопределённого интегралов.
- •§8. Замена переменной и интегрирование по частям в определенном интеграле.
- •§9. Несобственные интегралы.
- •1˚. Определение несобственных интегралов.
- •2˚. Основные свойства несобственных интегралов.
- •3˚. Сходимость интегралов от неотрицательных функций.
- •4˚. Интегрируемость степенных особенностей.
- •5˚. Абсолютная сходимость несобственных интегралов.
- •6˚. Признаки Абеля и Дирихле.
- •§10. Некоторые приложения определённого интеграла
- •1˚. Площадь фигуры (плоская мера Жордана).
- •2˚. Длина дуги кривой.
Глава 6.Определенный интеграл и его приложения. Несобственные интегралы. §1. Задачи, приводящие к понятию определённого интеграла.
1. Задача о площади
(или о квадратуре) криволинейной трапеции.
Пусть![]() − положительная функция. Требуется
найти площадь
− положительная функция. Требуется
найти площадь![]() фигуры, ограниченной графиком этой
функции, осью абсцисс, и отрезками
фигуры, ограниченной графиком этой
функции, осью абсцисс, и отрезками![]() .
.
Если
![]() ,
то
,
то![]() .
В общем случае это произведение зависит
.
В общем случае это произведение зависит![]() .
Оно даёт
.
Оно даёт![]() с ошибкой, доходящей
с ошибкой, доходящей![]() .
Здесь
.
Здесь![]() − колебание функции
− колебание функции![]() на отрезке
на отрезке![]() ,
т.е.
,
т.е.![]() ,
где
,
где![]()
![]() (Рис 1).
(Рис 1).

Для того, чтобы учесть изменение функции
![]() ,
разобьём отрезок
,
разобьём отрезок![]() на частичные отрезки
на частичные отрезки![]() ,
выберем
,
выберем![]() .
Тогда получим
.
Тогда получим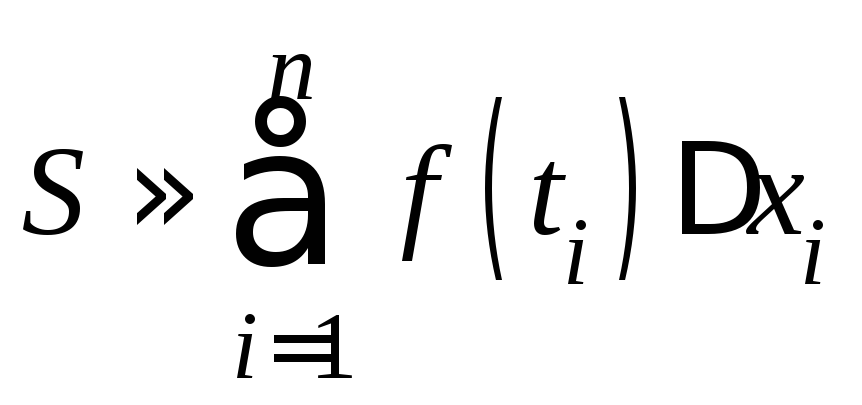 .
Ошибка сейчас не превышает суммы площадей
заштрихованных фигур на рисунке 2,
.
Ошибка сейчас не превышает суммы площадей
заштрихованных фигур на рисунке 2,
что значительно меньше, чем прежде.
Так как непрерывная функция мало изменяется при малых изменениях аргумента, то, по-видимому, точное значение площади равно
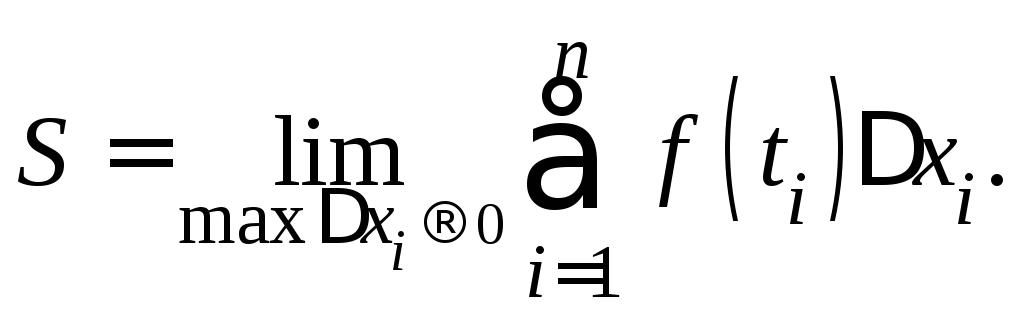
2. Та же конструкция возникает при вычислении перемещения точки, если известна её скорость.
3. Тот же предел суммы приходится рассматривать в задаче о нахождении массы (или заряда) стержня по известной линейной плотности массы (заряда) и т.д. и т.п.
§2. Два определения интеграла Римана.
1˚.Пусть![]() ;
;![]() −разбиениеотрезка
−разбиениеотрезка![]() .
Пусть далее
.
Пусть далее![]() ,
где
,
где![]() −набор промежуточных точек,
согласованный с разбиением
−набор промежуточных точек,
согласованный с разбиением![]() ;
;![]() −мелкость разбиения
−мелкость разбиения![]() ,
Наконец,
,
Наконец,![]() будет обозначать множество всех таких
наборов
будет обозначать множество всех таких
наборов![]() ,
согласованных с
,
согласованных с![]() .
.
Определение
1. Мы будем называть римановой интегральной суммойдля функции
римановой интегральной суммойдля функции![]() ,
соответствующей разбиению
,
соответствующей разбиению![]() и набору
и набору![]() .
.
Определение 2. Число![]() называется пределом интегральных сумм
при условии, что мелкость разбиения
стремится к нулю (в записи
называется пределом интегральных сумм
при условии, что мелкость разбиения
стремится к нулю (в записи![]() ),
если для любого числа
),
если для любого числа![]() найдется такое число
найдется такое число![]() ,
что при любых
,
что при любых![]() ,
для которых
,
для которых![]() ,
выполняется неравенство
,
выполняется неравенство![]()
Первое основное определение. Функция![]() называетсяинтегрируемой по Римануна отрезке
называетсяинтегрируемой по Римануна отрезке![]() или короче
или короче![]() ,
если существует предел
,
если существует предел![]() .
Сам предел
.
Сам предел![]() называетсяопределённым интегралом
Риманаи обозначается
называетсяопределённым интегралом
Риманаи обозначается![]() .
.
Отметим, что название “интеграл”
происходит от “integer” −
целый, а обозначение![]() подчеркивает происхождение из суммы
подчеркивает происхождение из суммы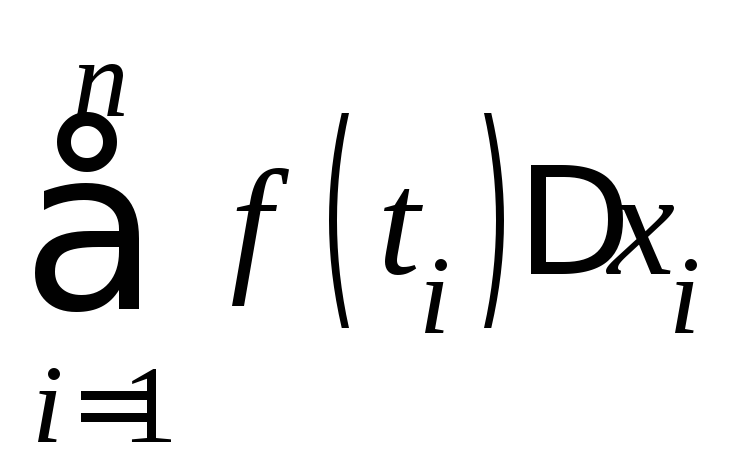 (
(![]() стилизованная
букваS).
стилизованная
букваS).
Теорема. (Необходимое условие
интегрируемости). Если функция
интегрируема на отрезке![]() ,
то она ограничена на этом отрезке.
,
то она ограничена на этом отрезке.
Доказательство. Предположим, что
функция![]() ,
но не является ограниченной. Существует
число
,
но не является ограниченной. Существует
число![]() ,
такое что
,
такое что![]() будет
будет![]() .
.
Фиксируем разбиение
![]() ,
для которого
,
для которого![]() .
Так как функция
.
Так как функция![]() неограниченна на отрезке
неограниченна на отрезке![]() ,
то она неограниченна на некоторых
частичных отрезках, скажем
,
то она неограниченна на некоторых
частичных отрезках, скажем![]() .
Фиксируем все
.
Фиксируем все![]() ,
,![]() ,
а само
,
а само![]() оставим пока неопределённым. Если
обозначить
оставим пока неопределённым. Если
обозначить![]() ,
то получим
,
то получим![]() .
Выберем теперь значение
.
Выберем теперь значение![]() так, чтобы
так, чтобы![]() было больше, чем
было больше, чем![]() .
Тогда окажется, что
.
Тогда окажется, что![]() .
А это противоречит выбору числа
.
А это противоречит выбору числа![]() .
.
2˚.Дальше мы будем рассматривать только ограниченные функции. Для каждой такой
функции
![]() и разбиения
и разбиения![]() можно определить величины:
можно определить величины:
![]() ,
,![]() ,
,![]() − колебание функции
− колебание функции![]() на отрезке
на отрезке![]() ,
а для отрезков разбиения
,
а для отрезков разбиения![]() полагаем
полагаем![]() ,
,![]() ,
,![]() .
.
Определение 3. Величина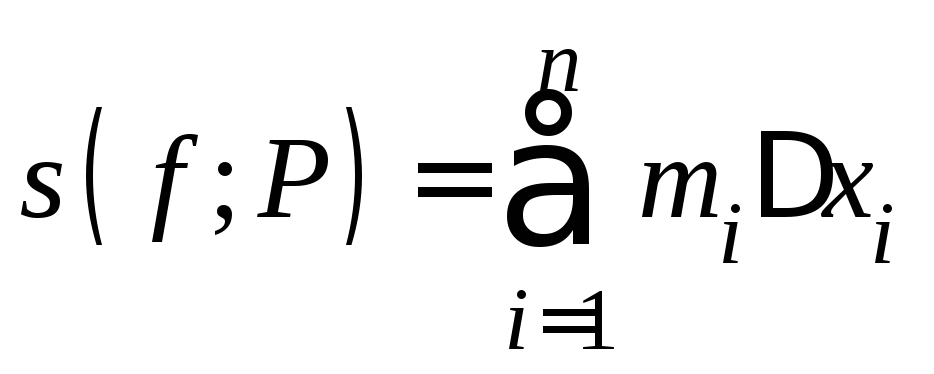 называетсянижнейсуммой Дарбу,
называетсянижнейсуммой Дарбу,
величина
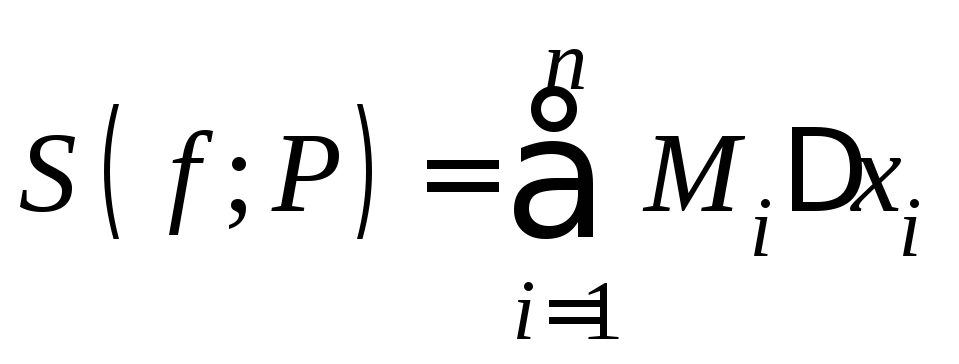 −верхнейсуммой Дарбу,
−верхнейсуммой Дарбу,
![]() называетсянижниминтегралом,
называетсянижниминтегралом,![]() −верхниминтегралом.
−верхниминтегралом.
Второе основное определение. Функция![]() называется интегрируемой на отрезке
называется интегрируемой на отрезке![]() ,
если
,
если![]() .
Их общее значение
.
Их общее значение![]() называется интегралом.
называется интегралом.
§3. Свойства сумм Дарбý.
Если ясно, о какой
функции
![]() идет речь, то мы будем писать
идет речь, то мы будем писать![]()
![]() ,
,![]() −
−![]() и
и![]() −
−![]() .
.
Теорема. Пусть![]() − ограниченная на отрезке
− ограниченная на отрезке![]() функция. Тогда для любого разбиения
функция. Тогда для любого разбиения![]() этого отрезка и любого набора точек
этого отрезка и любого набора точек![]() будет
будет
1)
![]() ,
,![]() и , значит,
и , значит,![]() ,
,![]() ;
;
2) если
![]() ,
то
,
то![]() и
и![]() ;
;
3)
![]() для любых двух разбиений
для любых двух разбиений![]() и
и![]() отрезка
отрезка![]() .
.
Упражнение.Доказать пункт 1) самостоятельно.
Доказательство пункта 2). Достаточно
рассмотреть случай, когда разность![]() состоит
ровно из одной точки, скажем,
состоит
ровно из одной точки, скажем,![]() .
Пусть
.
Пусть![]() − интервал из разбиения
− интервал из разбиения![]() ,
содержащий точку
,
содержащий точку![]() .
Обозначим
.
Обозначим![]() ,
,![]() ,
,![]() .
Тогда будет
.
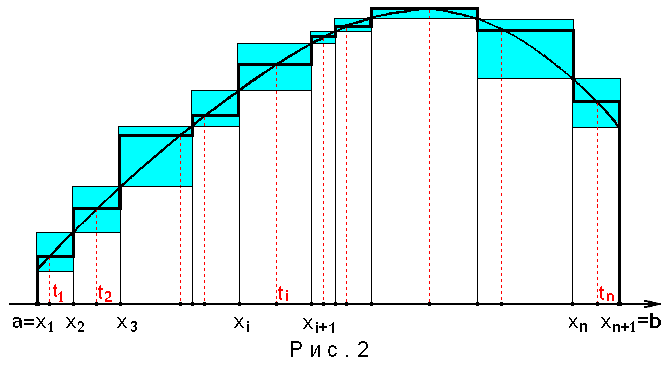
Тогда будет
![]()
![]() ,
,
т, е.
![]() (см. Рис. 3).
(см. Рис. 3).
Точно так же доказывается, что
![]() .
.
Доказательство пункта 3). Рассмотрим
вспомогательное разбиение![]() ,
Тогда из утверждений 1) и 2) сразу следует
,
Тогда из утверждений 1) и 2) сразу следует![]() .
.