Глава 4. Дифференциальное исчисление функций нескольких переменных. §1. Множества в пространстве . Непрерывные отображения.

1⁰. Мы имели дело раньше в основном с функциями вида,. Встречались мы и с кривыми, задаваемыми параметрическими уравнениями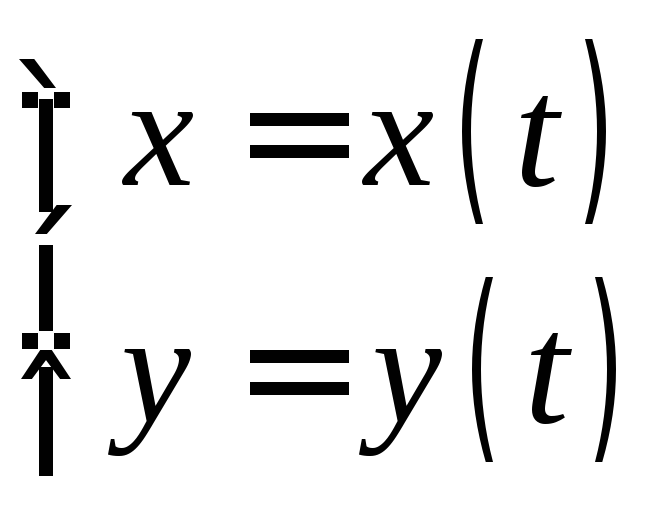. Здесь мы имеем.Это − отображение типа. В случае пространственной кривой получаем отображение типа. В геометрии приходится рассматривать поверхности с уравнением вида, то есть отображения типа.

Нам предстоит изучать отображения типа . Поэтому придется сначала познакомиться с множествами в.

−-мерное координатное пространство, Оно состоит из наборов действительных чисел. Мы будем рассматривать их и как векторы и как точки. Нулевым вектором называется вектор. Векторы можно покоординатно складывать и покоординатно умножать на скаляр. Длина вектора вычисляется по формуле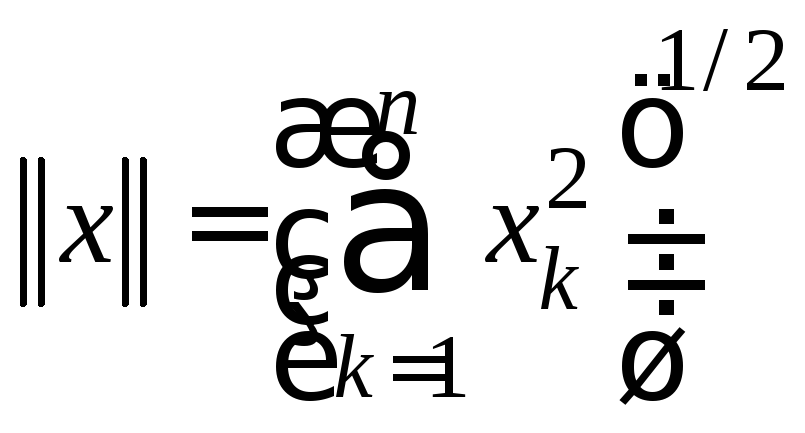. Напомним основные свойства функции.

1. при этомтогда и только тогда, когда.

2. для любого скаляра.

3. (неравенство треугольника).

Обобщением длины является норма. Это − любая числовая функция в, обладающая свойствами 1-2-3. Они называются аксиомами нормы. В качестве примера рассмотрим функцию. Можно доказать, чтоэта функция удовлетворяет аксиомам нормы.

Длина или евклидова норма − это ,,.

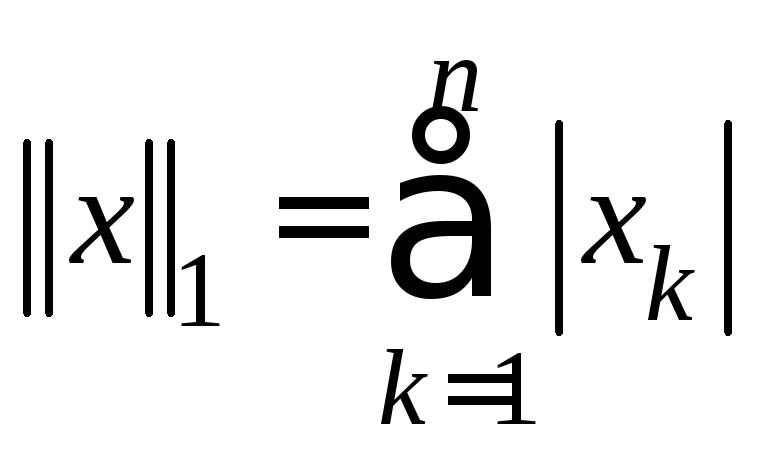Упражнение 1. Доказать, что.

Упражнение 2. Доказать неравенства: ,,.

Расстояниеммежду точкамииназывают величину.Открытым шаромв пространственазывается множество; точканазываетсяцентромшара, число− егорадиусом.

Упражнение 3. Нарисовать единичный шар (круг) на плоскостидля норм,и.

В дальнейшем будем писать просто.

Множество называетсяограниченным, если его можно покрыть некоторым шаром.

Последовательность точек называетсясходящейся(по норме), если существует точка, для которой(в записи). Последовательностьпокоординатно сходитсяк точке, если при каждом. Неравенства из упражнения 2 показывают, что покоординатная сходимость в пространстверавносильна сходимости по норме.

Точка называетсявнутреннейточкой множества, если существуеттакое, что. Множествоназываетсяоткрытым, если все его точки являются внутренними.

Точка называетсяпредельнойточкой множества, еслисуществует последовательность, которая сходится к. Множествоназываетсязамкнутым, если оно содержит все свои предельные точки.

Примеры. На числовой прямойинтервал− открытое множество, отрезок− замкнутое множество, а полуинтервални замкнут, ни открыт. В пространствешар− открытое множество.

Множество называетсясвязным, если любые две точки этого множества можно соединить ломанной, лежащей внутри этого множества.

В пространстве , как и в пространстве, справедлива теорема Больцано-Вейерштрасса и критерий Коши.

Теорема Больцано-Вейерштрасса. Из ограниченной последовательности можно выделить сходящуюся подпоследовательность.

Критерий Коши. Последовательностьсходятся тогда и только тогда, когда выполнено условие Коши, состоящее в том, что .

2⁰. Пусть, то есть− отображение типа. Мы скажем, что это отображениенепрерывнов точке, еслипри условии.

Упражнение. Пусть. Доказать, чтонепрерывно в точкетогда и только тогда, когда непрерывны все компоненты отображения.

Теорема Вейерштрасса о максимуме. Если функциянепрерывна в каждой точкеограниченного замкнутогомножества, тодостигает своего наибольшего (наименьшего) значения в некоторой точке этого множества.

Теорема Коши о промежуточном значении. Если функциянепрерывна в каждой точкесвязногомножества, тоне пропускает промежуточных значений.

3^o. Рассмотрим скалярную функцию, то есть отображение типа. Некоторое представление об изменениидают поверхности уровня (линии уровня). Это − множества с уравнением. В разных прикладных дисциплинах они носят разные названия: изотермы, изобары, горизонтали (в топографии).

Пример. Пусть. Сравним трехмерный график этой функции с плоским рисунком, изображающим её линии уровня.

Более подробный анализ поведения функции, как и в случае функций одного переменного, даёт дифференциальное исчисление.