15. Полупроводниковые диоды.

Полупроводниковым диодом называют нелинейный электронный прибор с двумя выводами. В зависимости от внутренней структуры, типа, количества и уровня легирования внутренних элементов диода и вольт‑амперной характеристики свойства полупроводниковых диодов бывают различными. В данном разделе будут рассмотрены следующие типы полупроводниковых диодов: выпрямительные диоды на основе p‑n перехода, стабилитроны, варикапы, туннельные и обращенные диоды.Характеристики идеального диода на основе p‑n перехода

Основу выпрямительного диода составляет обычный электронно-дырочный переход. Как ВАХ такого диода имеет ярко выраженную нелинейность, приведенную на рисунке 4.1а, б, и описывается уравнением (4.1). В прямом смещении ток диода инжекционный, большой по величине и представляет собой диффузионную компоненту тока основных носителей. При обратном смещении ток диода маленький по величине и представляет собой дрейфовую компоненту тока неосновных носителей. В состоянии равновесия суммарный ток, обусловленный диффузионными и дрейфовыми токами электронов и дырок, равен нулю.

Рис. 4.1. Параметры полупроводникового диода:а) ВАХ характеристика; б) конструкция корпуса ,(4.1)

.

Для анализа приборных характеристик выпрямительного диода важными являются такие дифференциальные параметры, как коэффициент выпрямления, характеристичные сопротивления и емкости диода в зависимости от выбора рабочей точки.

Выпрямление в диоде.Одним из главных свойств полупроводникового диода на основе p‑n перехода является резкая асимметрия вольт‑амперной характеристики: высокая проводимость при прямом смещении и низкая при обратном. Это свойство диода используется в выпрямительных диодах. На рисунке 4.2 схема выпрямления переменного тока в диоде.

Рис. 4.2. Схема, иллюстрирующая выпрямление переменного тока с помощью диода [10, 20]

Рассмотрим коэффициент выпрямления идеального диода на основе p‑n перехода. Для этого рассчитаем по уравнению (4.1) коэффициент выпрямления К как отношение прямого тока к обратному току диода при значениях напряжения U =  0,01 В; 0,025 В; 0,1 В; 0,25 В; 1 B. Получаем:.(4.2)

Величина  ^-1 при комнатной температуре составляет  В. Результаты расчета приведены в таблице.

VG, B	 0,01	0,025	0,1	0,25	1
K, отн. ед.	1,0	1,1	55	2,3·104	2,8·1020

При значениях переменного напряжения, модуль которого V_G меньше, чем тепловой потенциал kT/q, полупроводниковый диод не выпрямляет переменный ток. Коэффициент выпрямления достигает приемлемых величин при значениях V_G по крайней мере в 4 раза больших, чем тепловой потенциал kT/q, что при комнатной температуре Т = 300 К соответствует значению напряжения V_G =  0,1 В. Варикапы. Зависимость барьерной емкости С_Б от приложенного обратного напряжения V_G используется для приборной реализации. Полупроводниковый диод, реализующий эту зависимость, называется варикапом. Максимальное значение емкости варикап имеет при нулевом напряжении V_G. При увеличении обратного смещения емкость варикапа уменьшается. Функциональная зависимость емкости варикапа от напряжения определяется профилем легирования базы варикапа. В случае однородного легирования емкость обратно пропорциональна корню из приложенного напряжения V_G. Задавая профиль легирования в базе варикапа N_D(x), можно получить различные зависимости емкости варикапа от напряжения C(V_G) – линейно убывающие, экспоненциально убывающие.

16.Зонная диаграмма равновесного p-n-перехода. Условия равновесия. Контактная разность потенциалов p-nерехода.В состоянии равновесия, когда к переходу не приложено внешнее напряжение, через него протекают одновременно четыре различных тока. Запишем их, пользуясь величиной плотности тока j , т.е. тока, протекающего через единичное поперечное сечение: диффузионный ток дырок, обусловленный их движением из области р в область п ; - диффузионный ток электронов, связанный с движением электронов из области n в область р .Обе эти составляющие связаны с движением основных носителей под действием диффузии. Если бы не было ограничивающего фактора, диффузионные движения носителей продолжались бы до тех пор, пока концентрация электронов и дырок в обеих областях не выровнялась бы и мы бы уже не смогли различить ни р -, ни п -области. Таким ограничивающим фактором является внутреннее электрическое поле, возникающее в области перехода и ограничивающее диффузионные потоки носителей через переход. Образование этого поля связано с тем, что носители, диффундируя в соседнюю область (электроны – в р-область, дырки - в п -область), оставляют после себя неподвижные копы доноров и акцепторов. В результате п-область становится заряженной положительно, р-область - отрицательно, и возникают два слоя объемных зарядов, между которыми существует внутреннее электрическое поле, характеризующееся напряженностью (рис.2.2). Преодолеть тормозящее действие этого поля и проникнуть в соседнюю область совершающие диффузионное движение носители могут только в том случае, если они обладают достаточно большой энергией. В то же время внутреннее электрическое поле подхватывает в каждой области неосновные носители, которые, совершая тепловое движение, попадают на границы областей объемных зарядов, и переносят их в соседнюю область. Поэтому к указанным диффузионным токам, протекающим через переход, добавятся еще два: - дрейфовый ток дырок из областип в область p; - дрейфовый ток электронов из области р в область п .

Рис.2.2. Образование областей объемных зарядов в р- п -переходе.В состоянии равновесия сумма всех четырех указанных токов в р -п-переходе равна нулю: или полный ток через переход

Рис. 2.3. Распределение плотности объемного заядавдоль перехода.На рис.2.3 показано распределение плотности объемного заряда р в области р-п-перехода, х_п и х_р - границы областей объемных зарядов в п- и р-областях. Так как концентрации подвижных носителей заряда в области перехода понижены, то их при расчетах обычно не учитывают. Заряды в обеих областях равны по величине и противоположны по знаку. За пределами областей, при х< х_п и х>х_p концентрации свободных носителей заряда становятся соизмеримыми c концентрациеями йонов примеси, и, поэтому здесь можно считать.

Рис.2.4. Распределение потенциала вдоль перехода.На рис. 2.4 приведен график изменения потенциала в области p-n-перехода. Максимальная скорость изменения потенциала соответствует плоскости раздела областейp- и n-типа проводимости. За пределами областей положительного и отрицательного объемных зарядов будут потенциальные значения потенциалов вn-области и вp-области. Таким образом, иежду областями p- и n-типа существует контактная разность потенциалов .Поскольку напряженность электрического поля Е связана с потен­циалом, то в одномерном случае, когда изменение происходит только вдоль координаты х, ,можно построить зависимость Ё(х) в области перехода, которая показана на рис.2.5.

Рис.2.5. Распределение напряженности электрического поля вдоль перехода

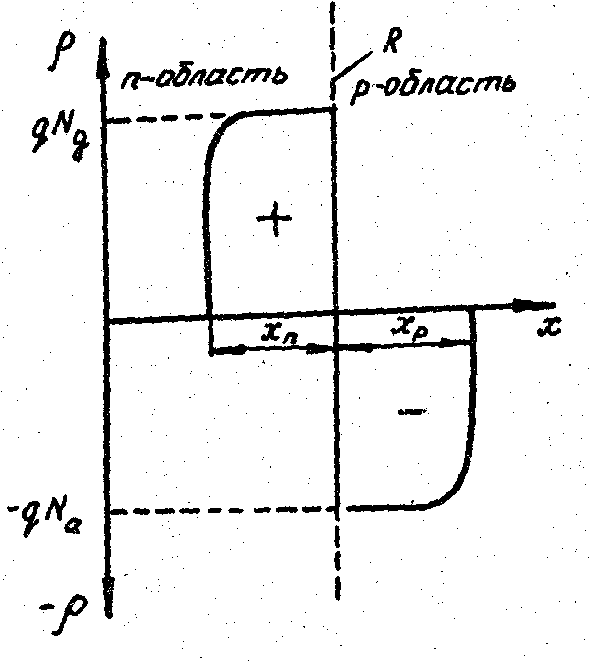Максимальное значение напряженности электри­ческого поля соответствует плоскости разделаR . Как уже говори­лось, внутреннее электрическое поле обусловлено наличием в об­ласти перехода объемных зарядов, а за его пределами при х< х_n и х>x_p р=0 и E=0. Значение Е_тах может быть определено из уравнения Пуассона:

(2.3), где -относительная диэлектрическая проницаемость полупроводникового материала; - диэлектрическая проницаемость вакуума(2.4)х_n и x_p - границы областей объемных зарядов.

Рис.2.6. Энергетическая диаграмма p-n-перехода.(По оси ординат отложены энергия E для электрона, которая увели­чивается снизу вверх, и энергия для дырки, которая . увеличивается сверху вниз).

На рис.2.6 представлена энергетическая диаграмма p-n-перехода. На границе раздела, в плоскости R, уровень Ферми проходит через середину запрещенной зоны, что соответствует случаю собственного полупроводника.

Диффузионный переход из области n в область p совершают электроны, имеющие энергии , а из областиp в область n – дырки с энергией . Дрейфовое движение осуществляется носителями, которые можно представить, прибегая к аналогии, скатывающимися с горки. При этом «скатываются» из областиn в область p, а электроны – из области p в область n.

Высота потенциального барьера схематически показана на рис.2.6.

Контактная разность потенциалов может быть выражена как

и будет тем выше, чем больше концентрации основных носителей в обеих областях. При увеличении концентрации основных носителей (степени легирования) уровень Ферми в n-областях стремится к , вp-области – к E_V и высота потенциального барьера на границе p-n-перехода стремится к ширине запрещенной зоны полупроводника.