
Лекции / Лекции (Павлова) / L26
.docЛекция № 26.
![]()
Др. формула которая позволяет оценивать значение этих функций:
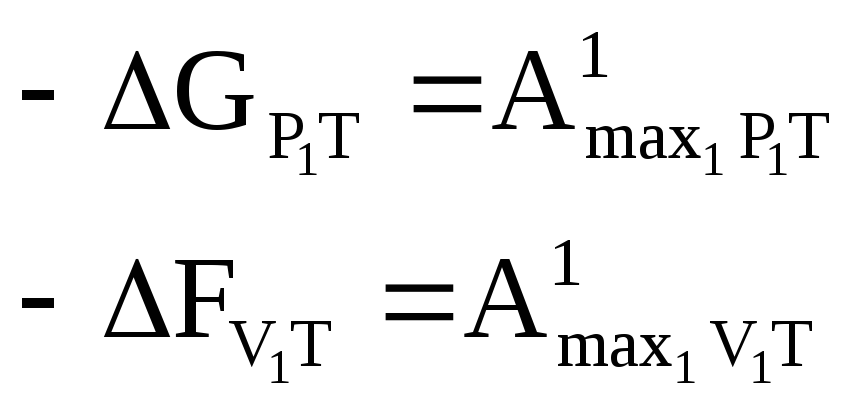
Такую работу можно осуществить в тех случаях, когда реакция идёт обратимым путём, но т.к. все реакции необратимы, то надо проводить реакции в гальваническом элементе (там реакции идут обратимы).
Гальванический элемент работает за счёт протекающего, а нём химического процесса
![]()

В
+
–
Работа эл. сил определяется напряжением на количество электричества. Для прохождения реакции Аmax полез осуществляемая в гальваническом элементе может быть рассчитана
![]()
Z – число
эквивалентов кот. соответствует одному
пробегу реакции (здесь число
![]() -ов
кот Zn отдаёт Cu)(т.е.
Z=2)
-ов
кот Zn отдаёт Cu)(т.е.
Z=2)
F – число Фарадея, оно равно 96484,156
Зная зависимость ЭДС от температуры можно рассчитать изменение энтропии при протекании токообразующей химической реакции.
![]()
![]() т.о. мы знаем на основании
данных ЭДС △G
и
△S реакции
можно рассчитать тепловой эффект
химической реакции
т.о. мы знаем на основании
данных ЭДС △G
и
△S реакции
можно рассчитать тепловой эффект
химической реакции

Но насколько надёжно мы оцениваем термодинамические параметры в гальваническом элементе.
![]() надёжная связь
надёжная связь
Но не соответствует справочным данным, всё зависит от того сколько мы отобрали электричества.
△H – кол-во тепла при реакции когда проводится крайнеобратимо.
![]()
![]()
Поэтому при определении △H в зависимости от отобрано эл-ва данные будут различны △H ненадёжная функция.
Уравнение Гиббса – Гельмгольца
Через
максимально полезную работу запишется
как:
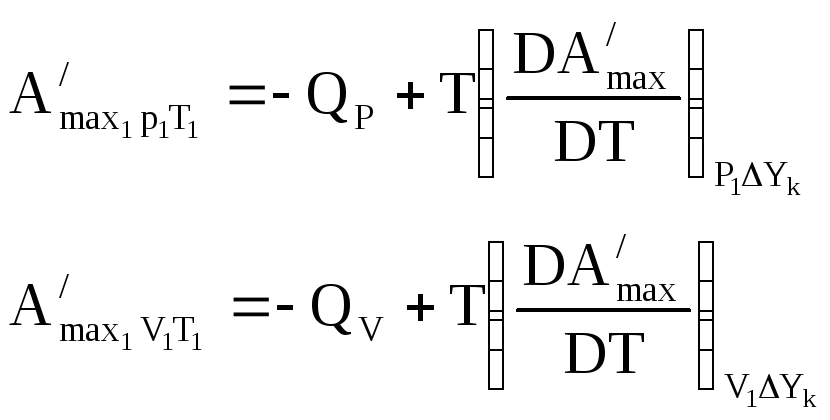
Положение которое характеризует взаимосвязи всех параметров.
Уравнение Гиббса – Гельмгольца связывает A’max с величиной температурного перехода из состояния 1 в 2 без совершения полезной работы. Теплота равновесного перехода равна T∆S=Qравн перепишем уравнение Гиббса – Гельмгольца в виде
A’max p,T=-Qp,равн+Qp,равн
A’max V,T=-QV,равн+QV,равн.
И![]() з
этих соотношений видно, что теплота
выделяемая при необратимом протекании
процесса, т.е. …. системой (-Qp
и -QV) не
обязательно полностью используется
для совершения работы при необратимом
совершении процесса Amax полез
может различным способом зависеть от
работы:
з
этих соотношений видно, что теплота
выделяемая при необратимом протекании
процесса, т.е. …. системой (-Qp
и -QV) не
обязательно полностью используется
для совершения работы при необратимом
совершении процесса Amax полез
может различным способом зависеть от
работы:
З Больше теплоты
выделяется в течение работы, избыток
А при
![]()
обратимом процессе за счет увеличения энтропии. При система отбирает теплоту у внешней среды. Еще более интересная ситуация при необратимом проведении эндотермических процессов, где ∆Нp,T0, ∆Up,T0. В этом случае единственной движущей силой самопроизвольного протекания процесса является увеличение энтропии, из химичсекого сродства вытекает:
∆G=∆H-T∆S
∆F=∆U-T∆S.
Для того чтобы процесс протекал самопроизвольно, надо чтобы T∆S∆H; T∆S>∆U.
Тепловой закон Нернста. (третье начало термодинамики).
В 1905г. Нернст в работе “о вычислении равновесия” ввел в термодинамику два постулата, которые не вытекают из 1 и 2 начал термодинамики. В своих выводах Нернст опирался на данные реакций идущих в гальванических элементах идущих при очень низких температурах и также о теплоемкостях материалов вблизи нуля.
Разница между функциями
()
![]()
![]() ∆F-∆U
∆F-∆U
() невелико и в близи нуля эта разница сближается не по линейному закону, а гораздо быстрее.
Постулаты уравнения. Г.-Г.
-
Производная сродства (∆G/T) и (∆F/T) не могут быть бесконечно большими при низких температурах при очень низких температурах значения (∆F и ∆U) и (∆G и ∆H) становится одинаковыми
т ()![]()
![]()
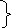
Р ()![]()
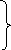
У![]() равнение
Гиббса-Гельмгольца.
равнение
Гиббса-Гельмгольца.
С U ()![]()
![]()
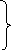
()=0.
Докажем:
правило Лапиталя![]()
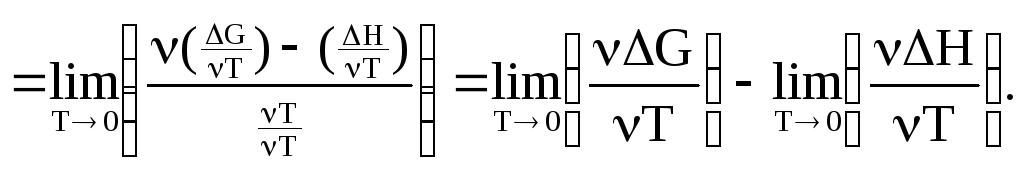
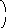 Сначала
откроем разницу вида:
Сначала
откроем разницу вида:
Из уравнения Гиббса-Гельмгольца вытекает, что
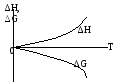
Графически представим
ход функции ∆G и ∆H вблизи температуры
абсолютного нуля. значит ![]()
![]()
![]()
![]()
![]()
Согласно
1 эта разность равна 0
При температуре, приближающейся к
абсолютному нулю, изотермические
процессы протекают без изменения
энтропии, значит при температуре
абсолютного нуля энтропия перестает
быть функцией состояния, она приближается
к а![]() бсолютной
величине не зависящей от параметров
системы.
бсолютной
величине не зависящей от параметров
системы.
Т.е. при Т близких к 0 энтропию системы нельзя изменить никаким воздействием на систему, поэтому нулевая изобара совпадает с изохорой.
Нет оснований считать, что теорема Нернста справедлива только для некоторых конденсированных веществ, она справедлива для всех веществ.
Следствие теоремы Нернста.
Ряд возможных следствий касающихся веществ вблизи абсолютного нуля, кроме того с ее с его помощью можно провести оценку некоторых энтропийных и химических констант.
-
П

– термический коэффициент расширения
оведение химических коэффициентов вблизи абсолютного нуля (коэффициент определит зависимость объема от температуры ).
И – термический
коэффициент давления![]()
Запишем полный дифференциал.
dG=-SdT-Vdp.
т.е. эта
взаимосвязь соотношений Максвелла![]()
Н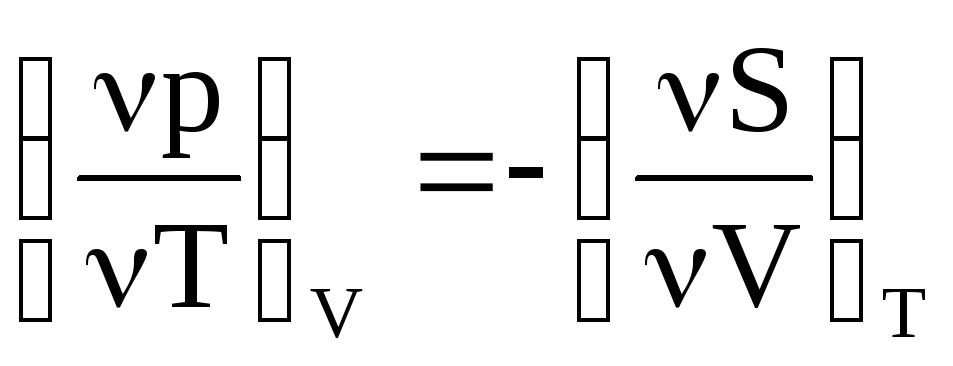
Используя эти взаимосвязь
перепишем значение для термических
коэффициентов
 о
т.к. при температурах близких к нулю
энтропия не зависит от p, V,
значит при Т0 0
и 0.
о
т.к. при температурах близких к нулю
энтропия не зависит от p, V,
значит при Т0 0
и 0.
