Лекции / Лекции (Павлова) / L24
.docЛекция №24.
Фундаментальное уравнение Гиббса.
Т/д потенциал как вспомогательная функция.
Запишем объединенное уравнение для второго и первого начал термодинамики и выразим из этого уравнения дифференциал внутренней энергии:
(*) dU
= TdS - pdV - de
- d
-
mgdh + …
полезные
работы
Это уравнение Гиббс назвал фундаментальным уравнением т/д.
Анализируя структуру (*), мы видим, что все слагаемые однотипны, т.е. p, V, m умножаются на изменение координаты (h, V, S). Поэтому перепишем
Отметим, что т.к. уравнение записано для обратимого процесса, то все переменные в нем относятся к системе (а не к внешней среде). Запишем математически форму дифференциала внутренней энергии:
U=δ(S, V, e, ,h …) По правилу дифференцирования в математике
(**) dU=(
)dS
+=(
)dV
+(
)dl
Сопоставляя (*) и (**) мы можем каждую из обобщённых сил приравнять частной производной внешней энергии:
T=(
)
;
- p=(
)
;
Вывод: здесь используются энтропия как переменная, но её нельзя измерить экспериментальным путём, поэтому в т/д вводятся вспомогательные функции.
Ф=U-
;
Ф как и энергия является функцией
состояния, мы знаем энтропию H=U+PV
– энергия растерянной системой, её
используют при анализе теплоты химической
реакции. Из других вспомогательных
функций приобрели большое значение
функции F-энергия
Гельмгольца, G- энергия
Гиббса.
U,H,F,G- четыре т/д потенциала.
Запишем выражения которыми определяется F и G.
F=U-TS
G=H-TS=U+PV-TS
Покажем схематически метод т/д потенциалами U,H,F,G.
H,
U, G – размерность энергии. Абсолютные значения
т/д потенциалов не известны
разрывы одинаковые всех функций.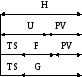
График характеризует определенное конкретное состояние системы. При изменении условий длины отрезков изменяются.
Получим значение дифференциала для F и G:
F = U - TS дифференцируем
dF = dU – TdS - SdT
dU = TdS – PdV -
dF=TdS-PdV-
-TdS-Sdt
dF= - Sdt – PdV -
F = (T,V,YK)
Т.о. функция F зависит от T, V и всех других YK. Аналогично для дифференциала G:
G = U – TS + PV дифференцируем:
dG = dU – TdS – SdT – PdV + VdP
dG = TdS – PdV -
+ PdV + VdP – TdS – Sdt = - SdT -
- VdP
G = (T,P,YK)
Энтропия системы через потенциал (энергию) Гельмгольца:
- S = (
)V,Y
;
- p = (
)S,V,Y
+Y
Запишем аналогичные производные через энергию Гиббса:
- S = (
)P,Y
;
V = (
)T,Y
;
Pi =
(
)S,P,X
G и F нужны, так как их изменение в процессе определяет работу системы.
Соотношение Максвелла.
Устанавливает взаимосвязи между различными производными свойств, характеризующих систему, получают их, используя выражения для т/д потенциалов (dU, dH, dF, dG). Запишем в качестве примера выражение для энергии Гельмгольца:
dF = - Sdt - PdV;
= 0; - S = (
)V;
- p = (
)T;
Так как dF- полный дифференциал функции Гельмгольца => равенство смешанных частиц производных второго порядка выполняется.
- (
)T
=
правая часть этих уравнений одна и та
же производная.
- (
)v
=
;
(
)T
= (
)v;
На основании этого соотношения можно получить уравнение Клаузиуса - Клайперона.
=
;
Связь т/д потенциалов с работой процесса.
Изменение т/д потенциалов – как критерий возможности самопроизвольного протекания процесса.
dU = TdS – pdV - A’
A’ – полученная работа;
а) обратимый процесс: совершаемая полученная работа имеет максимальное значение.
A’обр = A’max
A’max = TdS – pdV – dU
Известно, что система совершает работу до тех пор пока ее энергия не достигнет минимального значения, соответствующего заданным условиям критерием направленности системы является уменьшение энергии системы. Как только энергия = min состояние равновесия. Условия протекания процесса различны. В зависимости от этих условий мы по-разному можем находить максимальную полученную работу. Математически эта операция осуществляется путем интегрирования при постоянстве параметров системы.
Т.о. при p и V = const имеем:
A’max = - dUS,V
A’max = - ∆US,V
Вывод: в равновесных, обратимых процессах при S и V = const система A' = max равна убыли внутренней энергии системы.
б) необратимый процесс:
A’ < dTS – pdV – dU
A’необр A’max A’ < - dUS,V A’необр < - ∆US,V
В б) при S, V = const работа, совершаемая системой, меньше убыли внутренней энергии. Вывод ясен, т.к. часть энергии рассеивается в окружающую среду.
а) равновесный процесс:
dH = TdS – Vdp - A’max
A’max = - ∆HS,P
A’max = - ∆HS,P A’max = убыли энтальпии системы.
б) неравновесный процесс:
A’max < - ∆HS,P
A’max < - ∆HS,P
В б) при S и P = const совершаемая полезная работа меньше убыли энтальпии системы.
dF = -SdT – pdV - A’max , где pdV – механическая работа Amax.
dF = -SdT - A
А) 1) V, T закреплены
A’max = -dFT,V
A’max = -∆FT,V
2) T = const
A = -dFT
конечный процесс: A = - ∆FT
В равновесных процессах при V, T = const A’max (полезная) равна убыли энергии Гельмгольца системы.
В изотермическом процессе максимальная работа, совершаемая системой, равна убыли энергии Гельмгольца.
Б) необратимый процесс:
-
A’max < dFT,V A’max < - ∆FT,V
-
dAmax < dFT Amax < - ∆FT
Получаем работы меньше, чем хотели. Поэтому энергия Гельмгольца – свободная энергия Гельмгольца.
где
- ∆F - Amax -T∆S
– доля внутренней энергии, которая
никогда не может быть превращена в
работу – связанная энергия.
F = U – TS
∆
F
= ∆U – T∆S
- ∆U =- ∆F – T∆S
Т.о. существует два способа оценки внутренней энергии:
-
связь ∆F с max работой процесса:
- ∆F = Amax
-
через уравнение ∆F = ∆U – T∆S
-
- ∆F = Amax
-
∆F = ∆U – T∆S
d = - SdT + Vdp - A’max
а) A’max = - dGP,T
A’max = -∆GP,T
б) A’max < dGP,T
A’max < - ∆GP,T