
- •1. Некоторые сведения о флуктуациях
- •1.1 Флуктуации давления газа в камере
- •1.2. Флуктуации скорости частицы при движении в вязкой среде. Переход от механики Ньютона к статистической механике.
- •1.3. Флуктуации электрических величин и шумы в радиофизике
- •2. Способы описания шумов
- •2.1. Статистические характеристики случайного процесса
- •2.1.1. Математические характеристики шума.
- •2.1.2. Автокорреляцинная функция
- •2.1.3. Спектральная плотность мощности стационарного случайного процесса
- •2.1.4. Tеорема Винера-Хинчина
- •2.2. Широкополосные и узкополосные случайные процессы. Б171
- •2.3. Импульсные случайные процессы
- •2.4. Взаимная корреляционная функция и взаимный энергетический спектр
- •2.5. Коэффициент корреляции между двумя случайными напряжениями
- •2.6. Метод Ланжевена
- •3. Краткие сведения о флуктуациях в электронных приборах. Физические источники шумов в твёрдых телах
- •3.1. Тепловой шум.
- •3.1.1. Вывод формулы Найквиста
- •3.1.2. Обобщенная теорема Найквиста для линейного двухполюсника
- •3.1.3. Формула Гупта.
- •3.1.4. Квантовая модификация формулы Найквиста
- •3.1.5. Мощность тепловых шумов
- •3.1.6. Флуктуационно-диссипационная теорема
- •3.2. Шум горячих электронов (диффузионный шум).Шумовая температура.
- •3.3. Дробовой шум. Связь между дробовым шумом и зарядом носителей.
- •3.4. Генерационно-рекомбинационный шум в полупроводниках.
- •3.5. Шум вида 1/f (фликкер-шум)
- •3.6. 1/F шум
- •3.7. Взрывной шум или шум в виде случайного телеграфного сигнала.
- •3.8. Шумы, обусловленные равновесными температурными флуктуациями
- •3.9. Фотонный шум
- •3.10. Магнитные шумы.
- •3.10.1. Скачки Баркгаузена.
- •3.10.2. Изучение эффекта Баркгаузена.
- •3.10.3. Ограничение чувствительности магнитных датчиков и считывающих устройств из-за шумов Баркгаузена
- •3.11. Равновесные и неравновесные флуктуации
- •4. Некоторые сведения о флуктуациях в физиологии и других природных системах.
- •4.1. Магнитные флуктуации в природе
- •4.2. Флуктуации в биологии и физиологии
- •4.3. Стохастический резонанс
- •5. Преобразование шума в линейных цепях
- •6. Эквивалентные шумовые схемы
- •6.1. Эквивалентные шумовые схемы пассивного двухполюсника
- •6.2. Эквивалентные шумовые схемы четырехполюсников
- •6.3. Коэффициент шума усилителя и методы его измерения
2.1.4. Tеорема Винера-Хинчина
Энергетический спектр S(f) и автокорреляционная функция K() стационарного случайного процесса x(t) связаны друг с другом парой преобразования Фурье (теорема Винера - Хинчина). При этом энергетический спектр Sx(f) стационарного случайного процесса x(t) определяется как преобразование Фурье от автокорреляционной функции:
![]() ,
(2.16)
,
(2.16)
где = 2f – угловая частота, i – мнимая единица.
Автокорреляционная функция в свою очередь есть обратное преобразование Фурье от спектральной плотности мощности шума Sx (f).
![]() (2.17)
(2.17)
Поскольку автокорреляционная функция стационарного случайного процесса K() является четной функцией временного сдвига , последнее выражение можно преобразовать к виду, удобному для расчетов:
![]() (2.18)
(2.18)
Отсюда
при
= 0 (и при
![]() )
получим выражение для дисперсии случайной
величины x(t):
)
получим выражение для дисперсии случайной
величины x(t):
![]()
![]() =
=![]() ,
(2.19)
,
(2.19)
которая есть не что иное, как среднеквадратичное значение случайной величины x(t), а для случая электрических сигналов – мощность шума, выделяемая на сопротивлении 1 Ом.
Автокорреляционная
функция K()
и
энергетический спектр S(f)
стационарного
случайного процесса, как пара преобразования
Фурье, обладают всеми присущими этому
преобразованию свойствами. В частности,
чем шире эффективная
ширина спектра,
тем быстрее
изменяется значение флуктуирующей
переменной, и тем быстрее процесс
забывает свое начальное состояние, т.е.
с увеличением ширины полосы частот
энергетического
спектра
![]() время корреляции
время корреляции![]() уменьшается. Т.е., чем меньше ширина
функции корреляции случайного процесса
на оси временного сдвига,
тем шире его спектр. Для всех процессов
с одинаковой формой энергетического
спектра и, следовательно, с корреляционной
функцией одного вида произведение
уменьшается. Т.е., чем меньше ширина
функции корреляции случайного процесса
на оси временного сдвига,
тем шире его спектр. Для всех процессов
с одинаковой формой энергетического
спектра и, следовательно, с корреляционной
функцией одного вида произведение
![]() является некоторой константой.
является некоторой константой.
2.2. Широкополосные и узкополосные случайные процессы. Б171
Стационарный
случайный процесс с непрерывным
энергетическим спектром называют
узкополосным, когда спектр его сосредоточен
в относительно узкой полосе частот
![]() около
некоторой фиксированной частоты0
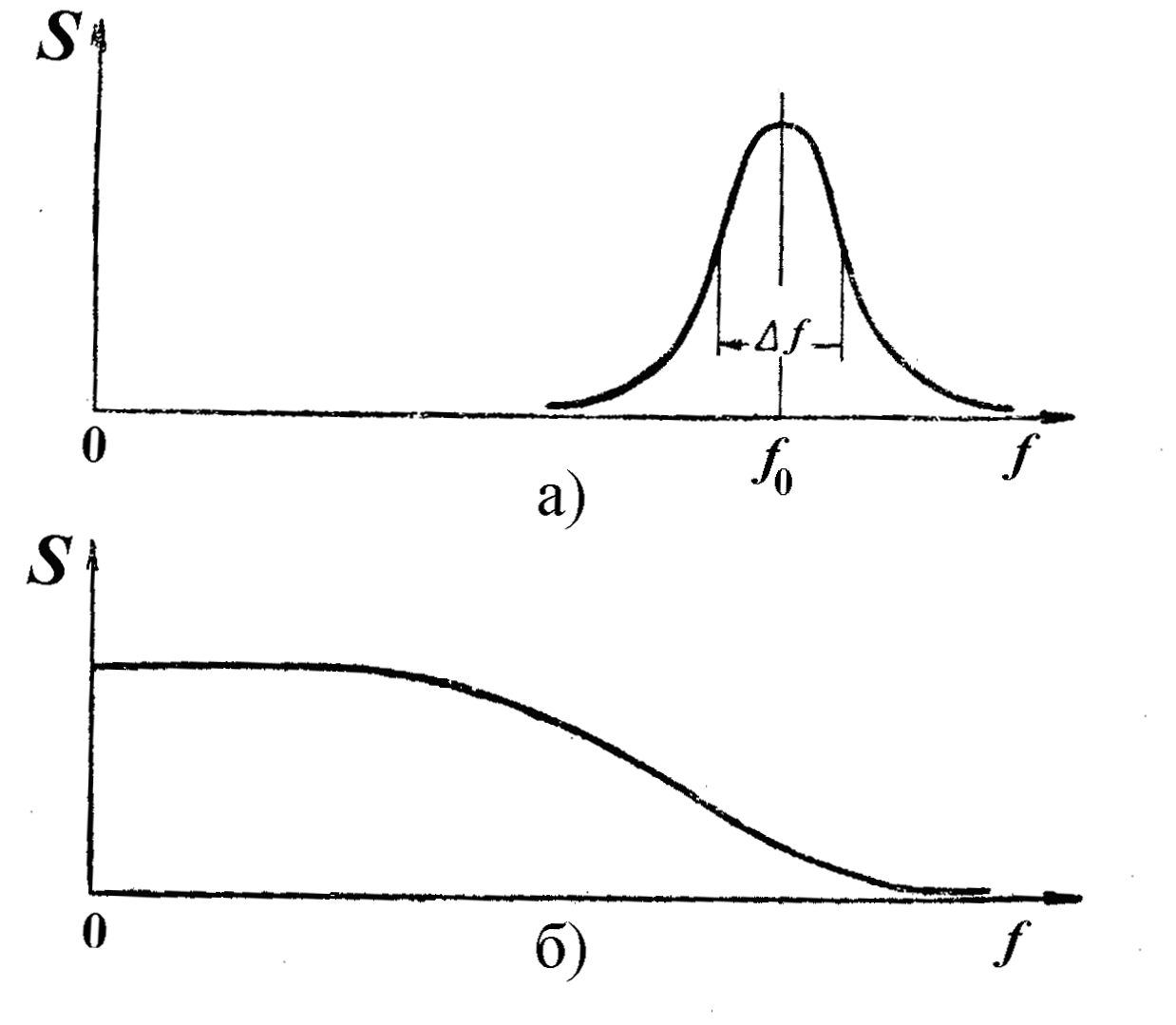
=2f0(рис. 2.4а), так что
условие узкополосности случайного
процесса имеет вид
около
некоторой фиксированной частоты0
=2f0(рис. 2.4а), так что
условие узкополосности случайного
процесса имеет вид
![]() ,или широкополосным,
когда указанное условие не выполняется
(рис. 2.4б).
,или широкополосным,
когда указанное условие не выполняется
(рис. 2.4б).
 S0
S0/2
S0
S0/2
Рис. 2.4. Энергетические спектры узкополосного (а) и широкополосного (б) случайных процессов.
Если узкополосный
шум подать на осциллограф и развертку
синхронизировать на частотах, кратных
центральной частоте полосы f0,
то реализация узкополосного случайного
процесса на экране осциллографа будет
похожа на синусоиду фиксированной
частотыf0(при
малой ширине полосы частот для
узкополосного шума![]() = 2-5 Гц). Близость к синусоиде имеет место
на протяжении довольно большого числа
периодовT =
1/f0.
= 2-5 Гц). Близость к синусоиде имеет место
на протяжении довольно большого числа
периодовT =
1/f0.
Для
энергетического спектра широкополосного
случайного
процесса S(![]() )
= 2S0
= const
в широком диапазоне частот. Хорошим
примером широкополосного случайного
процесса является белый шум, который
называют иногда дельта-коррелированным
случайным процессом, в связи с тем, что
функция корреляции для белого шума
согласно (2.17)
является
дельта-функцией, δ(τ):
)
= 2S0
= const
в широком диапазоне частот. Хорошим
примером широкополосного случайного
процесса является белый шум, который
называют иногда дельта-коррелированным
случайным процессом, в связи с тем, что
функция корреляции для белого шума
согласно (2.17)
является
дельта-функцией, δ(τ):
![]() =
=![]()
![]() δ(τ),
(2.20)
δ(τ),
(2.20)
где
δ(τ) -
функция равная нулю при всех значениях
τ
![]() иδ(0)
= ∞.
иδ(0)
= ∞.
Замена реального случайного процесса на δ-коррелированный в различных физических системах означает, что граничная частота спектра шумов не вводится в рассмотрение, поскольку она гораздо больше всех других частот, существенных для рассматриваемой системы.
Вместе
с тем для практики наиболее важное
значение имеет ограниченный по полосе
частот белый шум, энергетический спектр
которого согласно формуле (2.13)
аппроксимируется прямоугольником в
полосе частот ![]()
![]() ,как показано на
рис. 2.5.
,как показано на
рис. 2.5.
|
|
|
Рис.
2.5. СП белого шума в ограниченной полосе
частот |
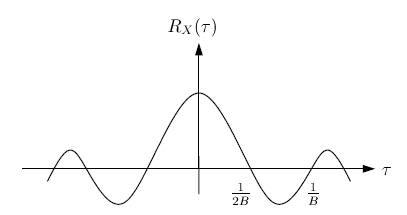
Для ограниченного по полосе частот белого шума автокорреляционная функция, рассчитанная по формуле (2.17), дается соотношением:
![]() ,
(2.21)
,
(2.21)
B=
![]()
Рис. 2.6. Автокорреляционная функция ограниченного по полосе частот белого шума.

