2.1.3. Спектральная плотность мощности стационарного случайного процесса

Наиболее важной характеристикой стационарных случайных процессов является спектральная плотность мощности, описывающая распределение мощности шума по частотному спектру. Рассмотрим стационарный случайный процесс, который может быть представлен беспорядочной последовательностью импульсов напряжения или тока, следующих друг за другом через случайные интервалы времени. Процесс со случайной последовательностью импульсов является непериодическим. Тем не менее, можно говорить о спектре такого процесса, понимая в данном случае под спектром распределение мощности по частотам.

Для описания шумов вводят понятие спектральной плотности мощности (СПМ) шума, называемой также в общем случае спектральной плотностью (СП) шума,которая определяется соотношением:

(2.10)

где P(f) - усредненная по времени мощность шума в полосе частотfна частоте измеренияf.

Как следует из соотношения (2.10), СП шума имеет размерность Вт/Гц. В общем случае СП является функцией частоты. Зависимость СП шума от частоты называют энергетическим спектром, который несет информацию о динамических характеристиках системы.

Если случайный процесс эргодический, то можно находить энергетический спектр такого процесса по его единственной реализации, что широко используется на практике..

При рассмотрении спектральных характеристик стационарного случайного процесса часто оказывается необходимым пользоваться понятием ширины спектра шума. Площадь под кривой энергетического спектра случайного процесса, отнесенную к СП шума на некоторой характерной частоте f₀, называютэффективной шириной спектра, которая определяется по формуле:

(2.11)

Эту величину можно трактовать как ширину равномерного энергетического спектра случайного процесса в полосе, эквивалентного по средней мощности рассматриваемому процессу.

Мощность шума P, заключенная в полосе частотf₁…f₂, равна

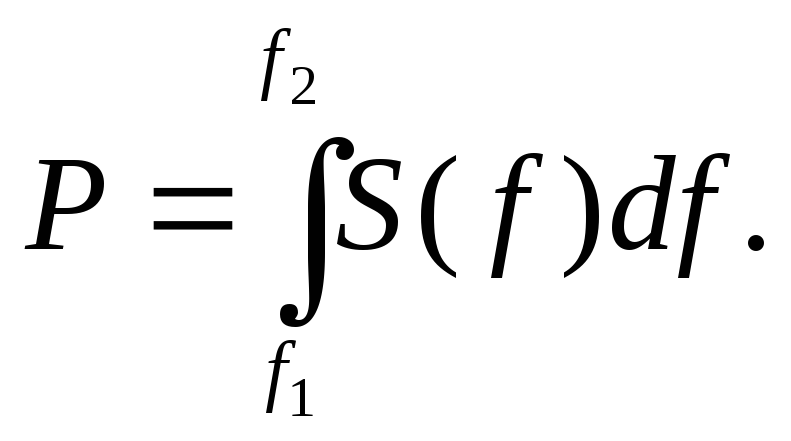(2.12)

Если СП шума в полосе частот f₁...f₂постоянна и равнаS₀, тогда для мощности шума в данной полосе частот имеем:гдеf =f₂-f₁– полоса частот, пропускаемая схемой или измерительным прибором.

Важным случаем стационарного случайного процесса является белый шум, для которого спектральная плотность не зависит от частоты в широком диапазоне частот (теоретически – в бесконечном диапазоне частот). Энергетический спектр белого шума в диапазоне частот -∞ < f < +∞ дается выражением:

= 2S₀ = const, (2.13)

Модель белого шума описывает случайный процесс без памяти (без последействия). Белый шумвозникает в системах с большим числом простых однородных элементов и характеризуется распределением амплитуды флуктуаций по нормальному закону. Свойства белого шума определяются статистикой независимых одиночных событий (например, тепловым движением носителей заряда в проводнике или полупроводнике). Вместе с тем истинный белый шум с бесконечной полосой частот не существует, поскольку он имеет бесконечную мощность.

На рис. 2.3. приведена типичная осциллограмма белого шума (зависимость мгновенных значений напряжения от времени) (рис. 2.3а) и функция распределения вероятности мгновенных величин напряжения e,которая является нормальным распределением (рис. 2.3б). Заштрихованная площадь под кривой соответствует вероятности появления мгновенных величин напряженияe, превышающих значениеe₁.

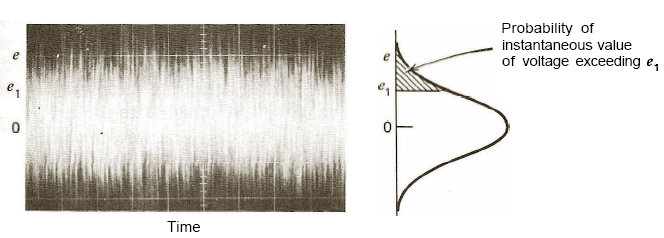
а) б)

Рис. 2.3. Типичная осциллограмма белого шума (а) и функция распределения плотности вероятности мгновенных величин амплитуды напряжения шума (б).

На практике при оценке величины шума какого-либо элемента или п/п прибора обычно измеряют среднеквадратичное шумовое напряжение в единицах В²или среднеквадратичный токв единицах А². При этом СП шума выражают в единицах В²/Гц или А²/Гц, а спектральные плотности флуктуаций напряженияS_u (f) или токаS_I (f) вычисляются по следующим формулам:

(2.14)

где и – усредненные по времени шумовое напряжение и ток в полосе частотfсоответственно. Черта сверху означает усреднение по времени.

В практических задачах при рассмотрении флуктуаций различных физических величин вводят понятие обобщенной спектральной плотности флуктуаций. При этом СП флуктуаций, например, для сопротивления Rвыражается в единицах Ом²/Гц; флуктуации магнитной индукции измеряются в единицах Тл²/Гц, а флуктуации частоты автогенератора – в единицах Гц²/Гц = Гц.

При сравнении уровней шума в линейных двухполюсниках одного и того же типа удобно пользоваться относительной спектральной плотностью шума, которая определяется как

= , (2.15)

где u– падение постоянного напряжения на линейном двухполюснике.

Как видно из выражения (2.15), относительная спектральная плотность шума S(f) выражается в единицах Гц^-1.