2.1.2. Автокорреляцинная функция

Среднее значение и дисперсия случайного процесса не описывают связи между величинами случайного напряжения в различные моменты времени. Для этого служит автокорреляционная (корреляционная) функция, которая показывает взаимосвязь случайной функции в различные моменты времени и которая является важнейшей характеристикой случайного процесса. В реальных системах изменение флуктуирующей величины не может происходить бесконечно быстро, и значения случайного процесса в разные моменты времени оказываются взаимосвязанными, т.е. шум обладает определенной памятью. Характеристикой шума, которая отражает связь между значениями случайного процесса в два различных момента времени, разделенные некоторым интервалом , и является корреляционная функция.

Рассмотрим стационарный случайный процесс x(t). Пусть x(t) случайная функция времени (случайный процесс), для которого среднее и дисперсия – постоянные величины, не зависящие от времени. Выделим два момента времени: t и t + . Автокорреляционная функция K() определяется как среднее по времени произведения случайных величин x(t) и x(t+) [1, 2]:

=. (2.7)

Автокорреляционная (корреляционная) функция есть мера продолжительности последействия флуктуаций, т.е. характеризует связь между предыдущими и последующими значениями случайной функции x(t).

Для стационарного случайного процесса среднее и дисперсия – постоянные величины, не зависящие от времени, а корреляционная функция зависит только от разности времен. Для большого числа практических задач корреляционная функция является достаточно полной характеристикой случайного процесса.

Автокорреляционная функция обладает следующими свойствами:

1. Автокорреляционная функция стационарного случайного процесса K() является четной функцией временного сдвига так что K() = K(-). Это следует из определения стационарного случайного процесса, т.е. из условия независимости его характеристик от начала отсчета времени.

2. Автокорреляционная функция зависит только от разности аргумента  = t ₂ – t₁. Вообще говоря, в статистической радиофизике случайный процесс называется стационарным в широком смысле, если его среднее и дисперсия не зависят от времени, а автокорреляционная функция зависит только от модуля временного сдвига ||.

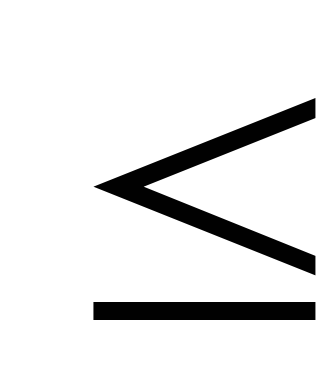
3. Автокорреляционная функция максимальна при = 0, т.е.K(0) ≥ K(). Если интервал временного сдвига стремится к нулю, флуктуации становятся одинаковыми, и корреляционная функция равна дисперсии шума:K(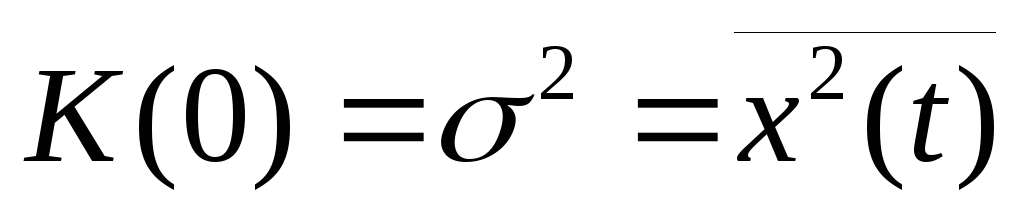) (присреднем значении случайного процесса равном нулю), т.е.

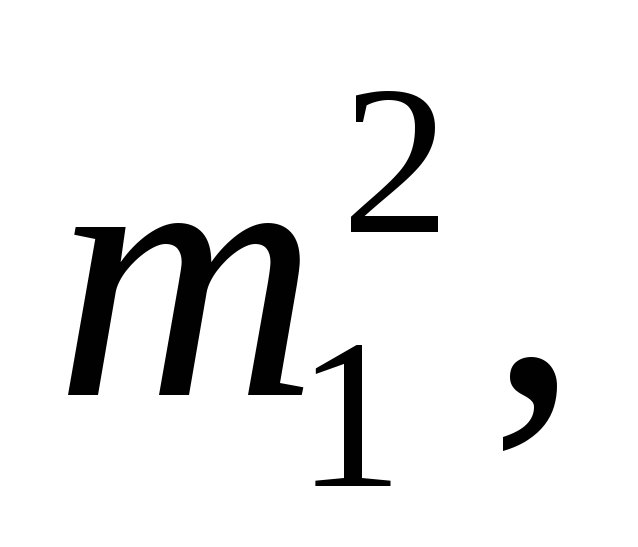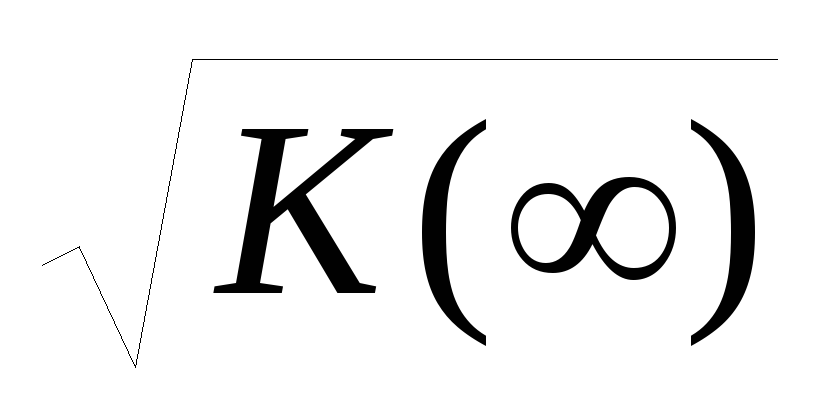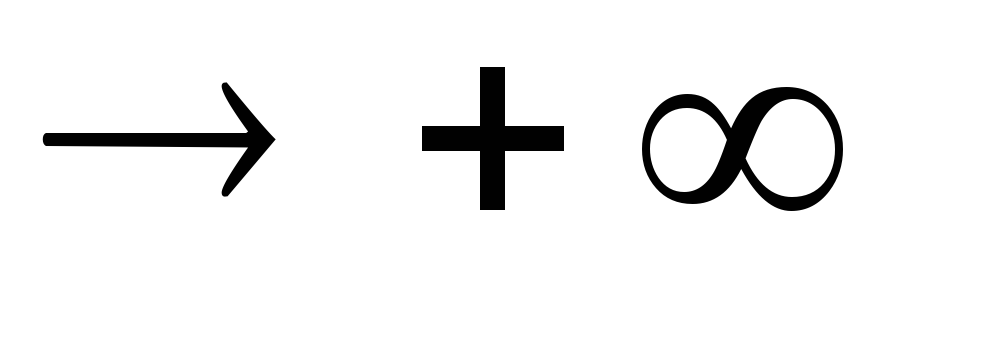4. В противоположном случае, когда интервал времени неограниченно возрастает, значения флуктуаций становятся взаимно независимыми, и, следовательно, корреляционная функция стремиться к нулю (присреднем значении случайного процесса равном нулю). Если же среднее значение случайного процесса m₁ не равно нулю, тогда т.е. среднее значение m₁ = . Для многих физических процессовK() при τи τ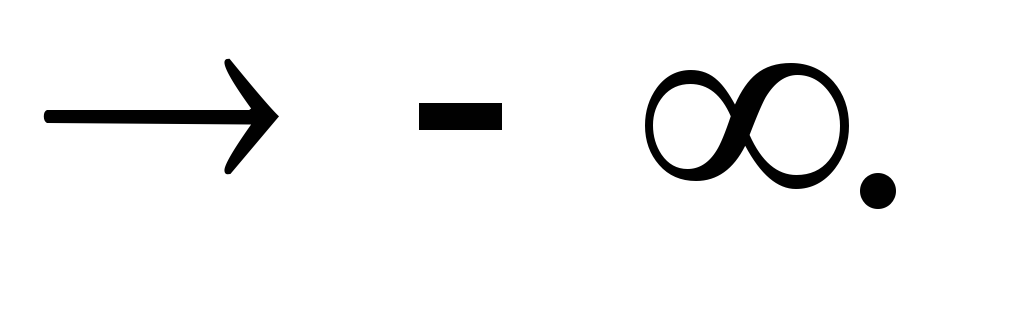Объясняется это тем, что многие физические процессы имеют конечное времяпоследействия флуктуаций, которое характеризует связь между значениями случайной функции x(t) в предыдущие и последующие моменты времени.

На рис. 2.2. приведена типичная зависимость автокорреляционной функции случайного процесса K() от временного сдвига , иллюстрирующая указанные выше свойства этой функции. Здесь значение функции корреляции .

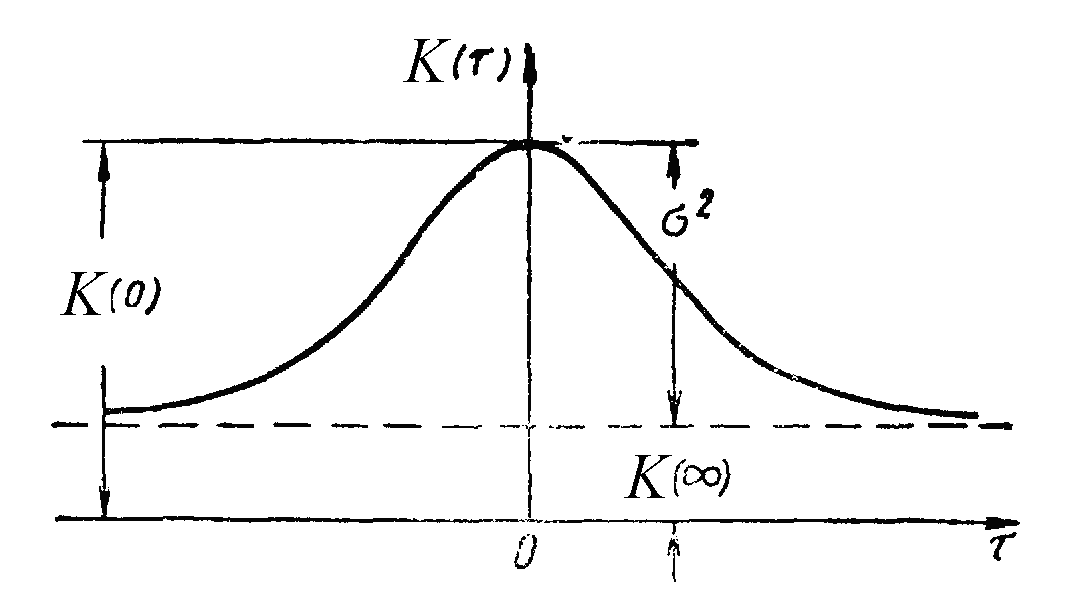
Рис. 2.2. Корреляционная функция стационарного случайного процесса.

Наряду с корреляционной функцией в теории случайных процессов вводят коэффициент корреляции стационарного случайного процесса, который определяется соотношением:

R_x(, (2.8)

где m₁ – среднее значение случайной величины x, а – дисперсия.

Параметр R_x(называют также нормированной корреляционной функцией. Необходимо помнить, что коэффициент корреляции, определяемый соотношением (2.8) – не простое число, а функция временного сдвига .

Если среднее случайного процесса m₁ равно нулю, тогда коэффициент корреляции (2.8) определяется соотношением:

R_x(. (2.8а)

Коэффициент корреляции R_x(обладает теми же свойствами, что и корреляционная функция. Он является четной функцией своего аргумента. Максимальное значение R_x(соответствует значению τ = 0, при котором R_x(= 1. При этом |R_x(1 при любом τ. Для чисто случайного процессаR_x()при.

Коэффициент корреляции стационарного случайного процесса может принимать нулевые значения и при конечном τ. Для стационарного случайного процесса всегда можно указать такое значение временного сдвига , при котором абсолютная величина коэффициента корреляции будет меньше некоторой заданной величины, например, при . Величина временного интервала , на котором значение корреляционной функции существенно отличается от нуля, то есть время, в течение которого сохраняется информация о начальных характеристиках процесса (память процесса), называется временем корреляции (или интервалом корреляции) случайного процесса (шума) .

В некоторых случаях время корреляции определяют следующим выражением:

(2.9)

Иногда время корреляции определяют как половина площади основания прямоугольника единичной высоты, площадь которого равна площади под кривой модуля коэффициента корреляции R_x(, т.е. определяется выражением:

(2.9а)

Если известна информация о поведении какой-либо реализации случайного процесса в настоящий момент времени, то возможен вероятностный прогноз случайного процесса на время порядка времени корреляции . Однако прогнозирование случайного процесса на время, значительно превышающее время корреляции, является безрезультатным, поскольку мгновенные значения случайной величины, столь далеко отстоящие по времени, практически некоррелированы, т.е. величина стремится к нулю при значении времени t >> .

Для белого шума время корреляции равно нулю, а корреляционная функция представляет собой - функцию. Подобный процесс является процессом без памяти, без последействия.