3.4. Генерационно-рекомбинационный шум в полупроводниках.

В полупроводниках и в приборах на их основе наблюдается еще один вид шума, создаваемый флуктуациями скоростей генерации и рекомбинации носителей, что приводит к флуктуациям концентрации свободных носителей. Этот вид шума, возникает в полупроводниковых приборах из-за присутствия в материале атомов примеси или нарушений кристаллической решетки, которые дают в запрещенной зоне (ЗЗ) полупроводника локальные ловушечные уровни. Рекомбинация и генерация носителей заряда через ловушки приводит к флуктуациям в полупроводнике концентрации свободных носителей, и как следствие, к флуктуациям проводимости (сопротивления) образца и к возникновению генерационно-рекомбинационного (ГР) шума. Концентрация свободных носителей (электронов), поставляемых в зону проводимости уровнем, расположенным в запрещенной зоне полупроводника, флуктуирует с постоянной времени жизни носителей .

Как известно, средняя концентрация свободных носителей (электронов или дырок), поставляемых в зону проводимости или в валентную зону, определяется концентрацией примесей в полупроводнике для данного уровня, положением уровня Ферми и температурой. Однако, в действительности, эта концентрация флуктуирует, и как следствие, концентрация носителей в зоне может быть и меньше, чем средняя (проводимость образца понижена), и больше, чем средняя (проводимость повышена). Постоянная времени обмена носителями между уровнем в ЗЗ и зоной проводимости определяется концентрацией носителей в зоне проводимости, сечением захвата уровня и температурой.

На рис. 3.7 показан ловушечный уровень E₀в запрещенной зоне (ЗЗ) полупроводника, поставляющий электроны в зону проводимости. Носитель (электрон) атакуетпотенциальный барьер высотой. Если полупроводник имеет один локальный ловушечный уровень в ЗЗ с энергиейE₀, тогда случайный процесс характеризуется одной постоянной времени(элементарный флуктуатор). При протекании через полупроводник с флуктуирующим числом носителейN токаI₀энергетический спектр ГР шума определяется выражением:

(3.32)

где N₀ – среднее равновесное число носителей в образце; N = N  N₀ , – усредненная величина квадрата флуктуаций числа носителейN,  - среднее время жизни носителей в полупроводнике,  = 2f - циклическая частота.

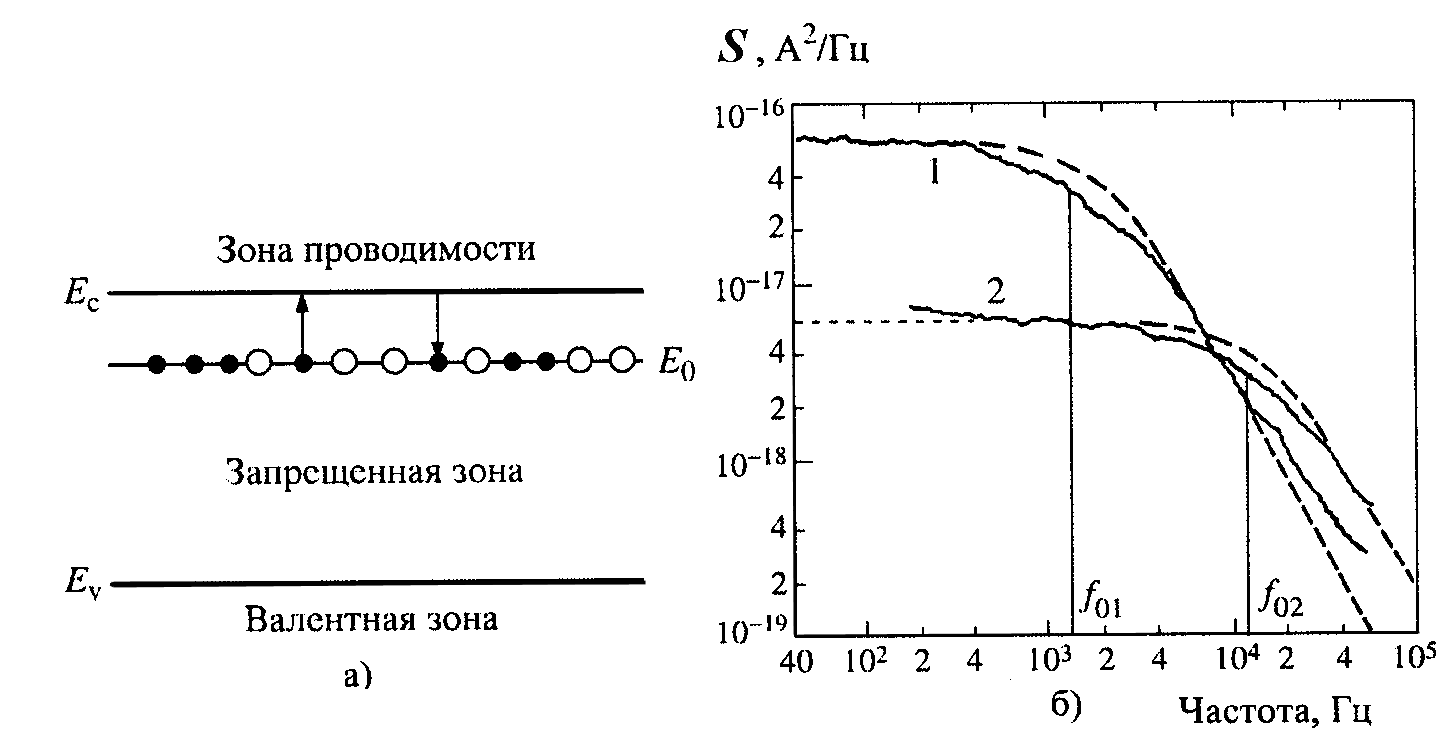
Рис. 3.7. Зонная диаграмма полупроводника с одним ловушечным уровенемE₀в запрещенной зоне, поставляющий (и захватывающий) электроны в зону проводимости.Убрать рис б)

Для некоторого объема полупроводника можно считать, что где– константа, слабо зависящая отN₀, но зависит от статистики носителей в образце. С учетом этого соотношения получим выражение для ГР шума, которое справедливо для самых общих случаев:

(3.33)

Это уравнение справедливонезависимо от того, какие процессы определяют флуктуации плотности и числа носителей заряда, а константазависит от свойств этих процессов.

Приняв, что отдельные процессы генерации и рекомбинации носителей являются независимыми, тогда для N будем иметь распределение Пуассона, для которого и в выражении(3.33) константа  = 1, что справедливо для многих практических случаев. При этом выражение для СП для ГР шума примет вид:

(3.34)

Как видно из этого выражения, уровень ГР шума зависит от числа носителей N₀ в полупроводником образце, т.е. при уменьшении размера образца уровень ГР шума возрастает.

На рис. 3.8 показан энергетический спектр ГР шума. Как следует из (3.32) при <<1 СП ГР шума является постоянной величинойS_gro= (4I)/N₀и не зависит от частоты. При²²>> 1S_gr(f)1/², т.е. СП спадает с увеличением частоты по квадратичному закону. Спектр вида(3.32)называют спектром Лоренца-Дебая или лоренцевским спектром, иногда – “Лоренцианом”. По частоте срезаf₁, на которойS_gr(f₁) = S_gro/2 (см. рис. 3.7), можно определить среднее время жизни носителей= 1/2f₁, поскольку в этом случае произведение в(3.34) , где=.

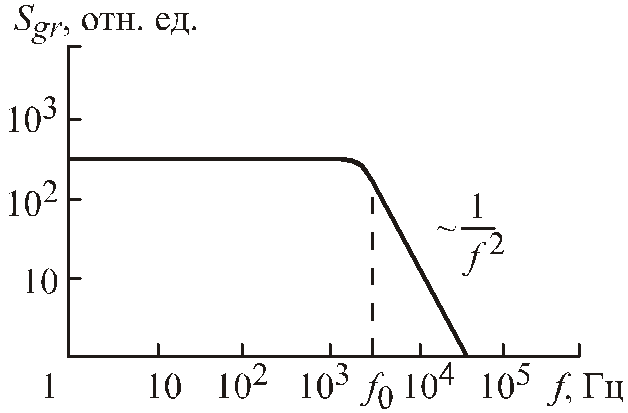
Рис. 3.8. Энергетический спектр ГР шума (спектр Лоренца-Дебая).

Постоянная времени преодоления электроном барьера  = 1/2f₀=₀exp(E_a/kT) уменьшается с ростом температуры. При этом концентрация электронов, преодолевающих барьер, флуктуирует с постоянной времени=₀exp(E_a/kT), вызывая тем самым флуктуации сопротивления образца.

На рис. 3.9 в качестве примера приведены экспериментальные зависимости энергетического спектра ГР шума для образца n-GaAsпри температуреТ= 241 К (кривая 1) и 293 К (кривая 2). Штриховые линии соответствуют классическим Лоренцианам.

Глубину залегания ловушечного уровня (энергию ионизации ГУ) в полупроводнике можно определить из температурной зависимости спектров ГР шума.

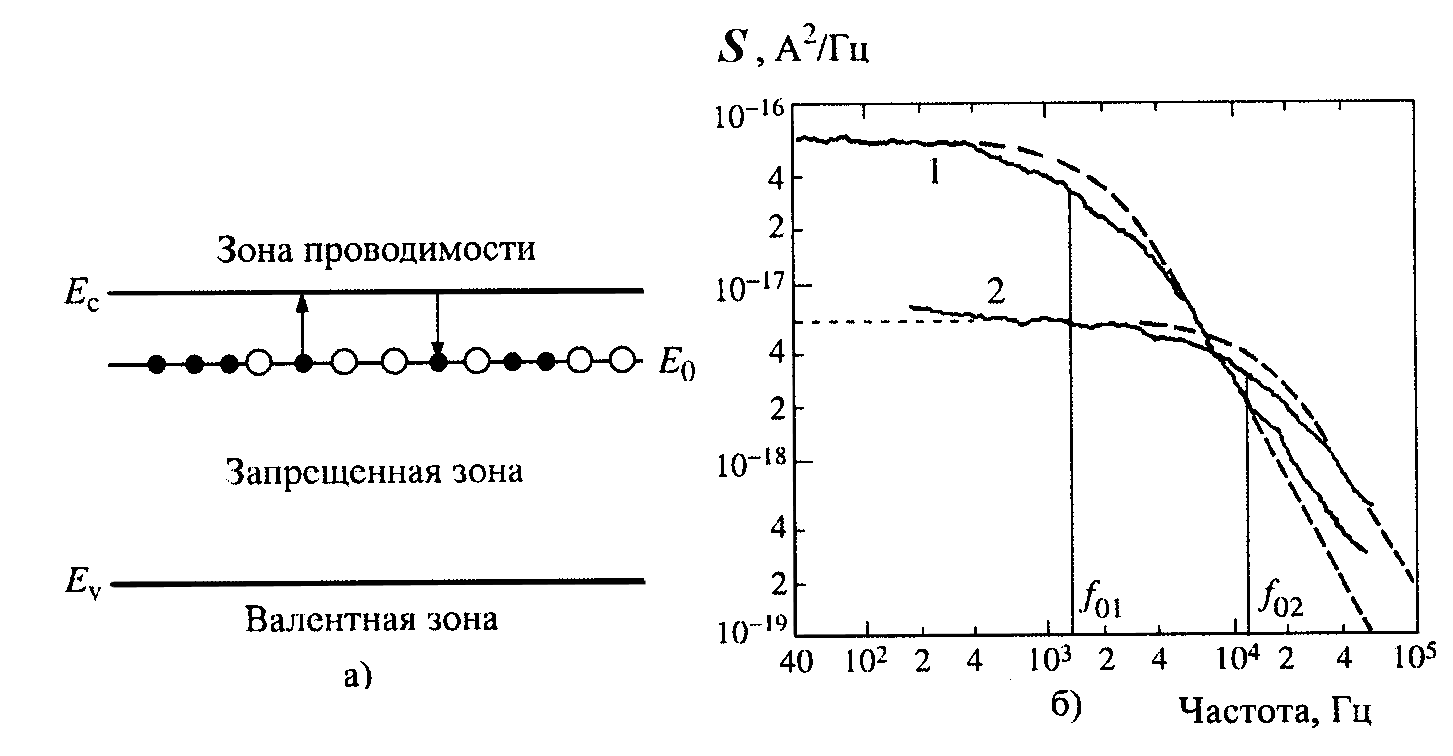
Рис. 3.9. Спектры токовых шумов для образца n-GaAsпри разных температурах: кривая 1 –Т= 241 К, кривая 2 –T= 293 К.Убрать рис а)

Если в полупроводнике имеется M генерационно-рекомбинационных уровней, различающихся по глубине залегания в запрещенной зоне, то имеет место суперпозиция ГР спектров (3.34), и тогда СП генерационно рекомбинационного шума полупроводника определяется выражением:

(3.35)

где A_i, _i - постоянные i-го ГР процесса.

В гетеропереходных полевых транзисторах (ГПТ) на основе слоев n⁺-Al_aGa_1-aAs-i-GaAsГР шум, возникающий вследствие обмена носителей заряда в канале с глубокими донорными уровнями (DX-центрами), может быть доминирующим источником шума.