Вопрос 27. Спиновая переменная волновой функции

Рассмотрим одну частицу – система с 3 степенями свободы. Задача решается в - представлении.

,

но есть еще внутренний параметр – спин, тогда

.

Здесь - переменная(пространственная координата) и(спиновая переменная, а именно проекция спина на ось).

Здесь мы рассматриваем стационарную задачу, поэтому отt не зависит.

Скалярное произведение теперь запишем в виде

Вероятность обнаружения частицы в объемевблизи точки:

Если хотим найти реализацию конкретного значения :

Рассмотрим действие операторов в пространстве четырех переменных

Было известно

(*)

Обобщим (*) на случай четырех переменных:

(**)

Рассмотрим случай когда действует только на спиновую переменную. В этом случае ядро будет следующим

и интеграл (**) переходит в интеграл:

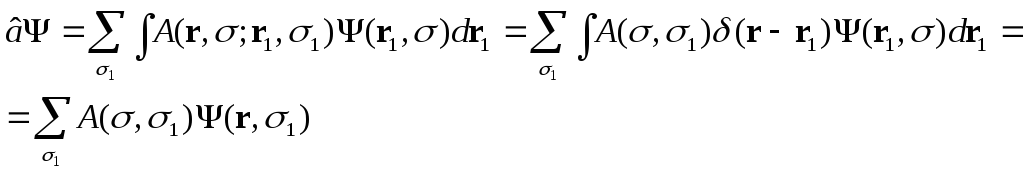
Тогда

Переменная здесь не играет большой роли. В дальноейшем будем ее опускать, тогда

Функция имеет 2s+1 переменную.

Ядро в дискретных переменных вырождается в матрицу, т. е. это есть матрица размером .

Вопрос 29. Принцип тождественности.

Этот принцип в квантовой механике определенным образом связан с принципом Гайзенберга.

Если рассмотрим ансамбль одинаковых частиц, то идентификация этих частиц невозможна.

Одинаковые частицы обладают всеми одинаковыми внутренними свойствами (m, e, s, …). Мы не можем в квантовой механике ввести траекторию, тогда не можем различить одинаковые частицы.

Например, в электронном газе не отдельные частицы, а целый ансамбль. В такой системе – тождественные частицы.

В ансамбле одинаковых частиц реализуются состояния, инвариантные относительно их перестановок.

Т. к. частицы идентифицировать невозможно, то мы не можем различить состояния, которые вызваны перестановкой частиц.

Вопрос 28. Оператор перестановки и его свойства

Введем обозначение оператор, который осуществляет перестановкуa-ой и b-ой частицы из ансамбля одинаковых частиц.

Оператор для таких систем из одинаковых частиц обладает симметрией.

Так как частицы одинаковые, то они имеют одинаковую энергию взаимодействия, т. е. она инвариантна относительно перестановки.

Т. е. можно записать

(*)

Так как оператор явным образом от времени не зависит, то из (*) следует, что он является интегралом движения. Его собственные значения сохраняются.

Найдем собственные значения оператора .

Запишем задачу Штурма-Лиувилля:

(**)

При повторном действии оператора , получим:

(***)

С учетом (**):

Тогда из (***)

, .

Получаем частицы с симметричными и антисимметричными волновыми функциями: бозоны и фермионы.

Кроме того, оператор - это интеграл движения. Тогда его собственные значения сохраняются во времени. Т. е. свойства волновых функций, связанных с действием этого оператора тоже сохраняются.

Функции отвечающие собственному значению +1 называются симметричными, описывают симметричные состояния.

Аналогично

Это антисимметричная функция.

Свойства симметричности и антисимметричности называются интегралами движения, т. е. сохраняются. Ансамбль не может переходить из одного состояния в другое (т. е. из симметричного в антисимметричное и наоборот).

Симметричные функции описывают состояние систем с целым спином, т. е. ансамбль бозонов.

Антисимметричные функции – ансамбль фермионов.

Пусть

, где ,,.

Мы будем рассматривать стационарные состояния, т. е.

,где .

Стационарные функции удовлетворяют стационарному уравнению Шредингера

, так как операторы икоммутируют, то

.

Мы имеем

Если всего N частиц, то можно осуществить N! перестановок, тогда имеем N! возможных функций .

Так как все удовлетворяют уравнению Шредингера при одной и тойже энергии , то мы получили вырождение. Оно носит фиктивный характер. Для того чтобы избавиться от этого вырождения проведем симметризацию функций.