Вопрос 31. Симметричное и антисимметричное состояния.

Чтобы построить конкретные функции будем рассматривать ансамбль независимых частиц, т. е. они между собой не взаимодействуют, но могут находиться во внешнем поле.

Для i-ой частицы во внешнем поле:

Так как частицы одинаковые, то их массы одинаковые, т. е. .

Полный оператор

(*)

Для одинаковые аналитические выражения (закон один), но здесь разные координаты.

Когда оператор представим в виде (*), то можно провести разделение переменных

.

Тогда уравнение

разбивается на N одинаковых уравнений:

- волновая одночастичная функция.

- это набор квантовых чисел, характеризующих одночастичное состояние.

Тогда

(**)

- это все квантовые числа, относящиеся к рассматриваемому ансамблю.

Причем , где .

Учтем действие оператора перестановки:

1. Рассмотрим симметричные состояния.

Однако из (**) при перестановке мы получаем другую функцию. Но в (**) функция еще не симметричная. Симметризуем ее:

Здесь сумма по всем нетождественным перестановкам частиц.

- постоянная нормировки

, где .

Рассмотрим случай двух частиц

Для данного случая .

Так как бозоны могут находиться в неограниченном количестве в одном и том же состоянии, то здесь когда говорим о нетождественных состояниях, то имеем в виду, что эта перестановка приводит к новому состоянию.

Если перестановка происходит в одном и том же состоянии, то она тождественная и выбрасывается из рассмотрения. Для бозонов из N! перестановок тождественные перестановки. Тогда надо рассматриватьперестановок, гдеN всего бозонов, а в 1-ом состоянии находится N₁ частиц, во 2-ом N₂ частиц и тд.

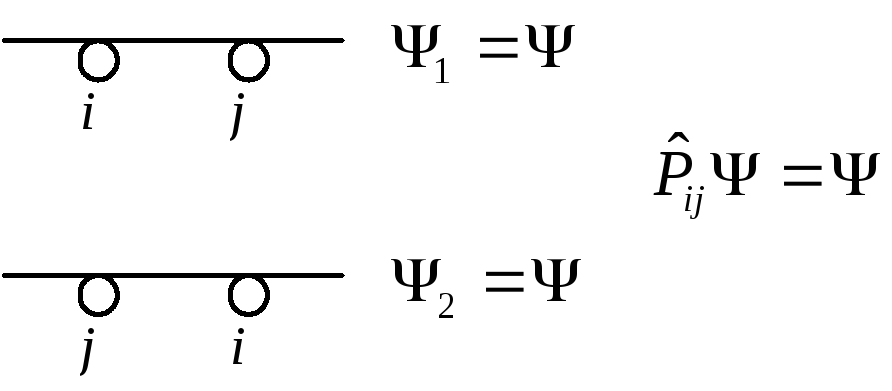
Симметричные состояния допускают произвольное число частиц в одночастичном состоянии.

Тогда нормировочный множитель

2. Рассмотрим антисимметричные состояния

Здесь

(***)

Чтобы учесть знак вводят понятие парной (соседней, элементарной) перестановки.

Пусть надо переставить в ряде цифры 1 и 4. Учтем элементарные перестановки: 2134, 2314, и т. д.

Здесь 5 элементарных перестановок. .

Тогда в сумму (***) надо поставить .

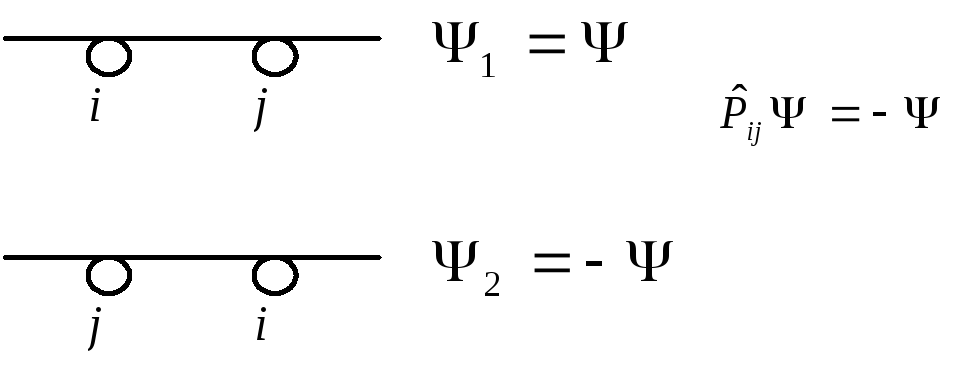
Если i и j в одном состоянии, то ,=> .

Антисимметричные состояния запрещают нахождение более одной частицы в одночастичном состоянии.

В сумме (***) оператор это оператор не элементарной перестановки, а какой-то конкретной перестановки.

Итак получаем из (***) выражение

Рассмотрим пару частиц, тогда

Эта функция обладает свойством антисимметричности. Подействуем на нее оператором перестановки:

, т. е. - собственная функция оператора перестановки.

Здесь т. к. у фермионов в каждом одночастичном состоянии число частиц не превышает 1, т. е. 0 или 1.

В наиболее общем виде

.

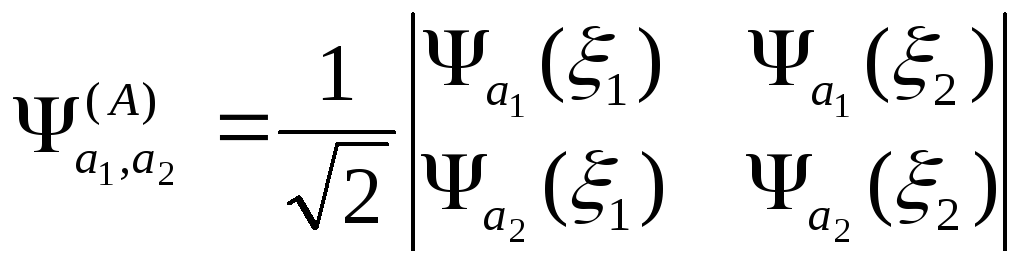Обобщим

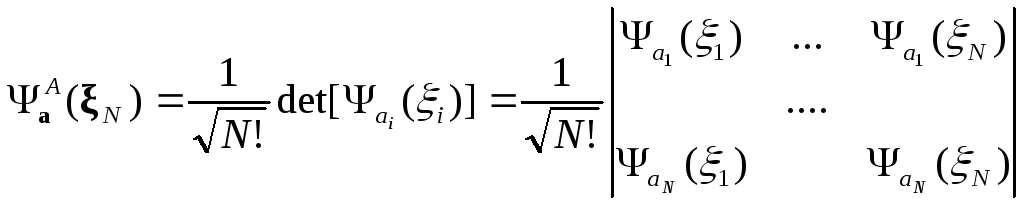
Из этого вида вытекает принцип Паули: не более одного фермиона может находиться в одном квантовом состоянии.

Допустим две частицы в одном квантовом состоянии, тогда у них совпадают квантовые числа, т. е. . Тогда для детерминанта имеем 2 одинаковые строки, он равен нулю. Состояние не реализуется.

Вопрос 25. Стационарная теория возмущений в случае невырожденного дискретного энергетического спектра: нулевое и первое приближения.

Рассмотрим оператор , который обладает дискретным спектром:

Под номером понимается набор всех квантовых чисел, опереляющих состояние системы.

- значения образующие энергетический спектр.

Так как спектр невырожденный, то между состоянием и уровнем (энергией) существует взаимооднозначное соответствие, т. е.:

.

Т. к. спектр дискретный, то функции квадратичноинтегрируемы:

/

Пусть ЗШЛ решена и найдены собственные функции и собственные значения.

Рассмотрим ЗШЛ: .

Оператор здесь имеет такую структуру, что эта ЗШЛ просто не решается, как ЗШЛ для оператора.

Оператор должен:

1. иметь структуру 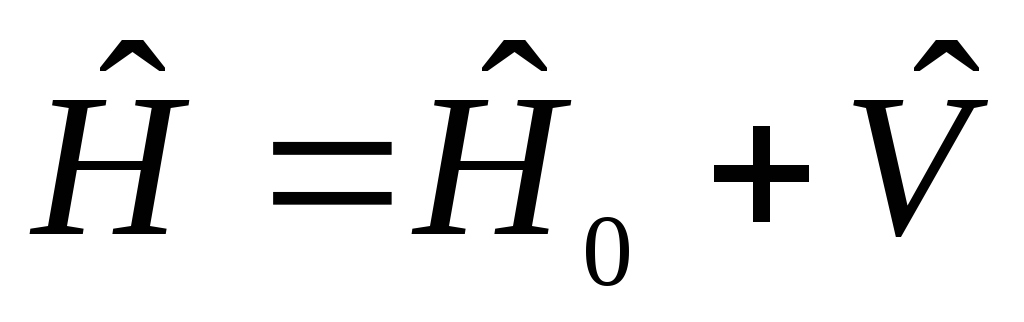, где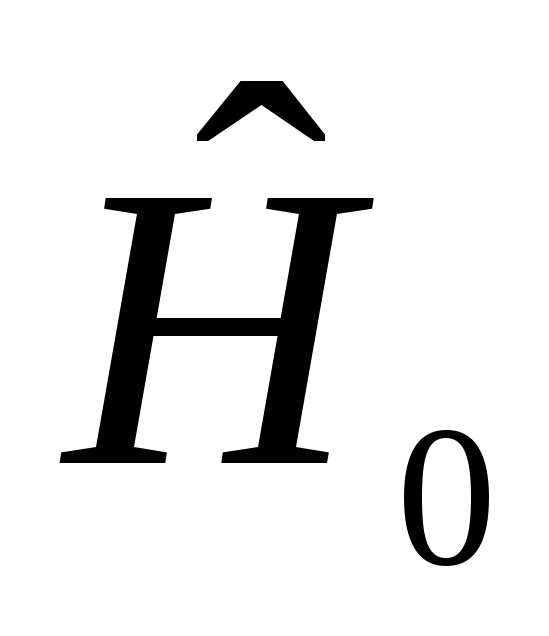- оператор для которого задача решена.,- дает малую добавку в оператор.

2. Спектр собственных функций дискретен, тогда собственные функции квадратичноимнтегрируемые

.

Решим задачу разложения по малому параметру (через теорию возмущений).

Из этого получаем

(*)

т.к. параметр малый, то энергетический спектр можно разложить по малому параметру:

p – указывает порядок разложения и показывает малость члена суммы.

отвечает невозмущенной задаче

.

- поправка имеющая первый порядок малости.

Т. к. собственные функции оператора образуют базис, то по ним можно разложить собственные функции возмущенного оператора

.

(**)

Коэффициенты разложения:

Их можно разложить по малому параметру:

Теперь задача теории возмущений состоит в нахождении членов рядов:

(***)

Чем больше членов рядов найдем, тем точнее решим задачу.

Подставим (**) в (*) и вынесем коэффициенты за знак операторов

Используем решение для невозмущенного оператора

Обозначим этот ряд , где, тогда.

Используем соотношение

.

Коэффициенты выносятся за знак скалярного произведения:

Рассчитаем

.

- это матричный элемент оператора возмущений, который рассчитывается по невозмущенным функциям.

Тогда имеем

.

Получили матричное уравнение, которое должны разложить по малым параметрам и прировнять 0 все слагаемые соответствующие своим порядкам малости.

считается величиной первого порядка малости, по нему проводится разложение.

Используем, что , здесь

Тогда(4*)

Получили исходное уравнение. К нему еще добавляются две нормировки:

, (1)

(2)

Подставим в уравнение (4*) выражения (***)

(3)

Группируем члены по порядку малости. По каждому порядку должны получать справа ноль.

Сначала нулевой порядок

Так как имеет первый порядок малости то член связанный с ним будет отсутствовать.

Из этого выражения получаем что, так как спектр невырожденный, при даети получаем, а при,может быть.

Легко видеть, что так как

,

то нулевое приближение дает

.

Тогда в нулевом приближении имеем решение:

Теперь для уровней:.

Окончательно в результате нулевого приближения

Перейдем к первому приближению.

Получим дополнительные соотношения из условия нормировки возмущенных функций.

Так как ,,

Получим .

Подставим сюда разложение по малому параметру

,

тогда имеем

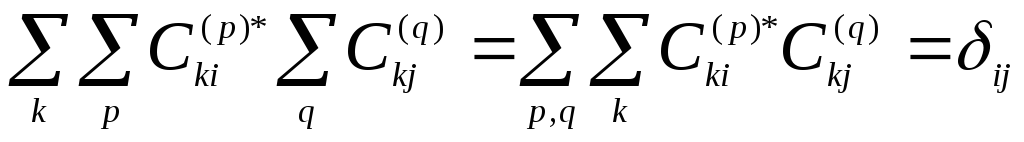
Здесь справа стоит величина нулевого порядка малости.

Для , .

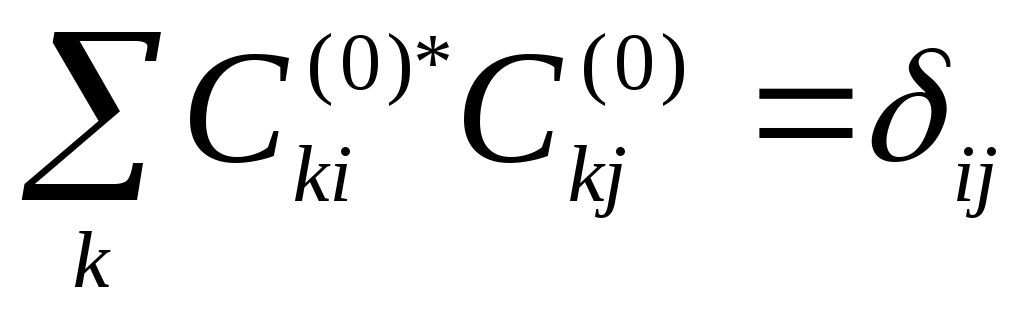
Для

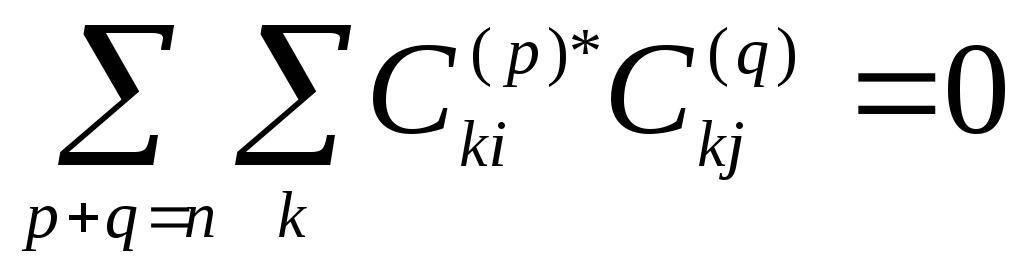(5*)

Рассмотрим первое приближение: . Два случая и,и.

(6*)

Из (5*) имеем

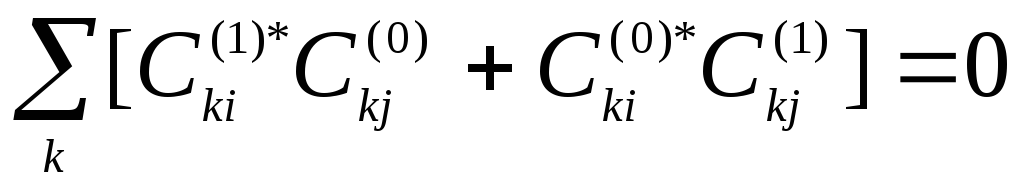(7*)

Используем, что

Тогда из (6*) и (7*):

. (8*)

Из (8*) рассмотрим случай :

- поправка к i-ому энергетическому уровню первого порядка малости

Тогда в первом приближении

и также получаем .

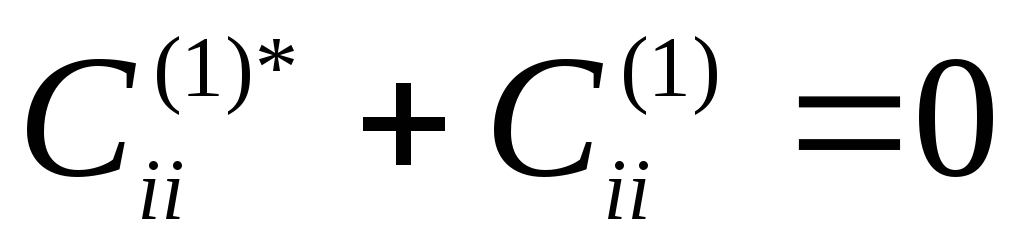Тогда получили, что

,

т. е. коэффициенты чисто мнимые.

Ввиду неопределенности фазового множителя при волновой функции, то полагают

, тогда принимают .

Из (8*) рассмотрим случай .

.

Подставим это выражение в (8*) и проверим условие нормировки:

.

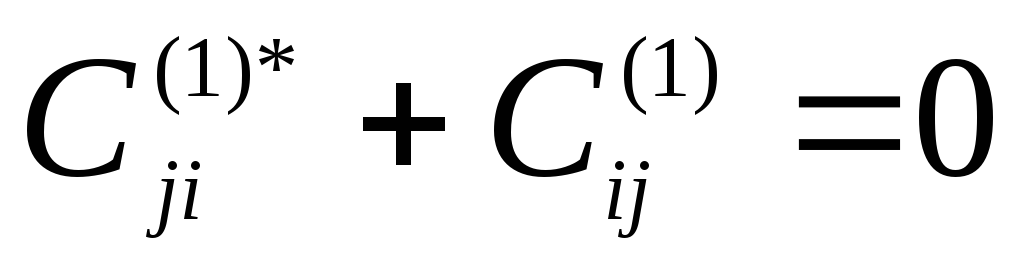Распишем

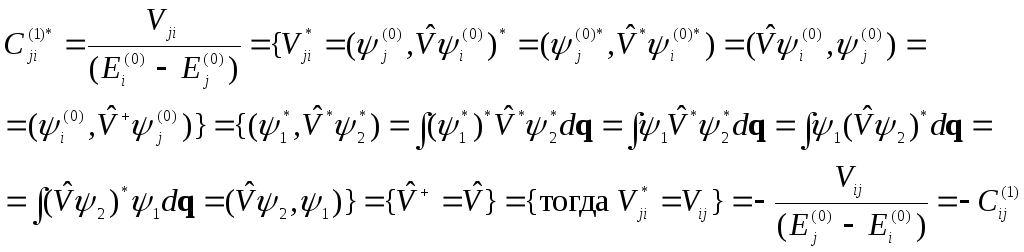Получили истинность условия нормировки.

Тогда в первом приближении теории возмущений получили:

.

Нам необходимо найти волновые функции, для них