Если , то операторы коммутативны.

Если , то операторы не коммутативны.

Так как физические величины вещественны, то число операторов в квантовой механике сужается.

Сужение класса операторов – эрмитовость операторов.

Запишем определение среднего:

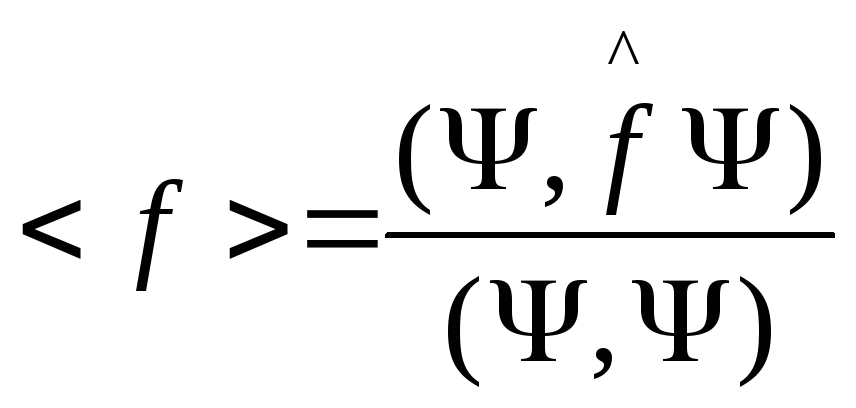
Так как результаты измерений вещественны, то тоже должно быть вещественным, т.е.

(5)

тогда

,

т.е.

Обозначим , тогда

Тогда из (5) получаем

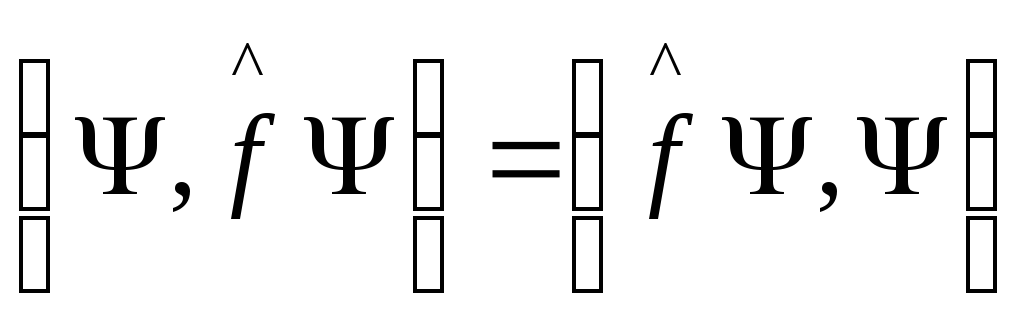(6)

Из (6) имеем для любых :

,,

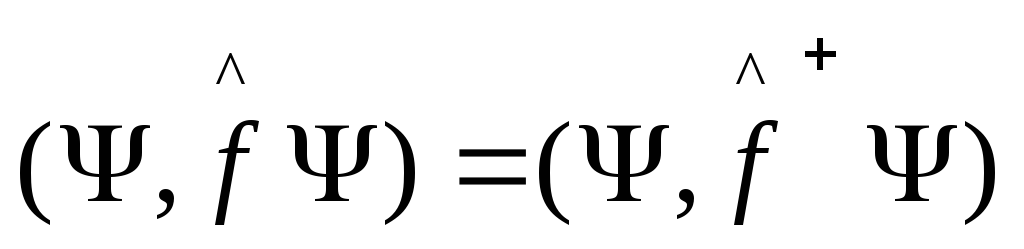где 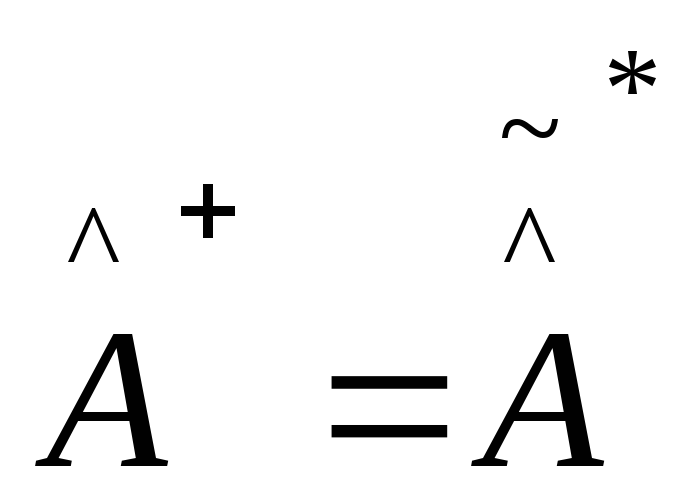(сопряженный и транспонированный)

Вопрос 10. 11. Собственные функции и собственные значения эрмитовых операторов. Случаи дискретного и непрерывного спектров.

Начнем с дискретного спектра, т.к. ему соответствует квадратичноинтегрируемые функции.

Задача Штурма-Лиувилля дискретного спектра

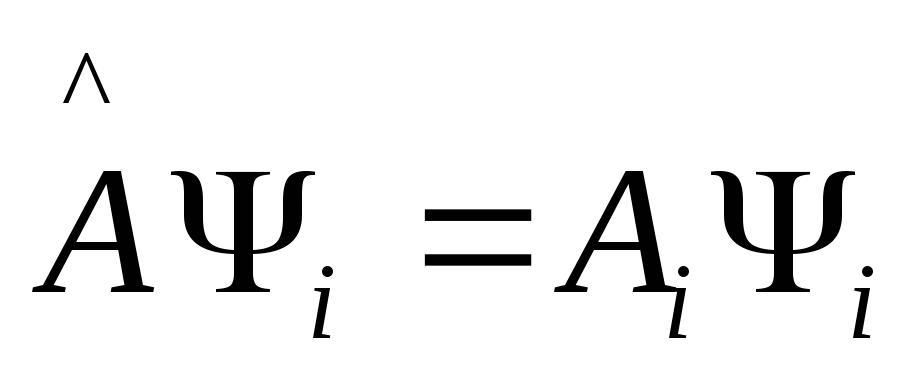(1)

-собственные функции

- собственные значения

Так как эрмитов, то его собственные значения вещественны.

Расчет среднего . Если речь идет о физической величине, тоэто волновые функции (описывающие состояние системы). Если речь идет о математическом аппарате, то- это любые функции.

Как частные случай рассмотрим , где- собственные функции оператора. Тогда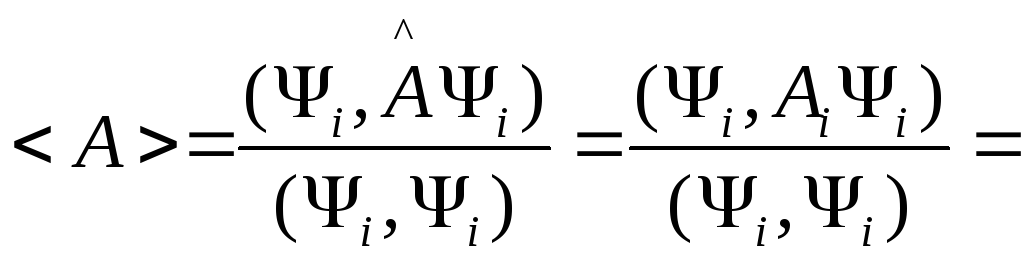

{Так как - число, то его можно вынести за знак скалярного произведения}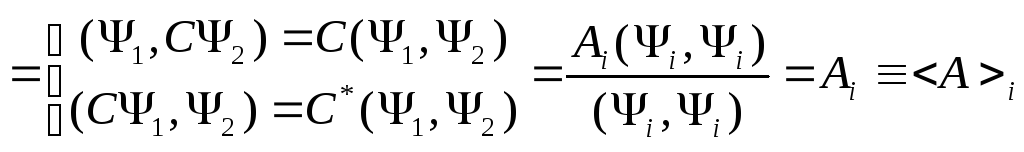- это среднее значение величинывi-ом квантовом состоянии.

Так как среднее – вещественно, то и собственные значения вещественны.

Для эрмитова оператора собственные значения вещественны. Все эрмитовы операторы имеют вещественные спектры.

Рассмотрим теперь

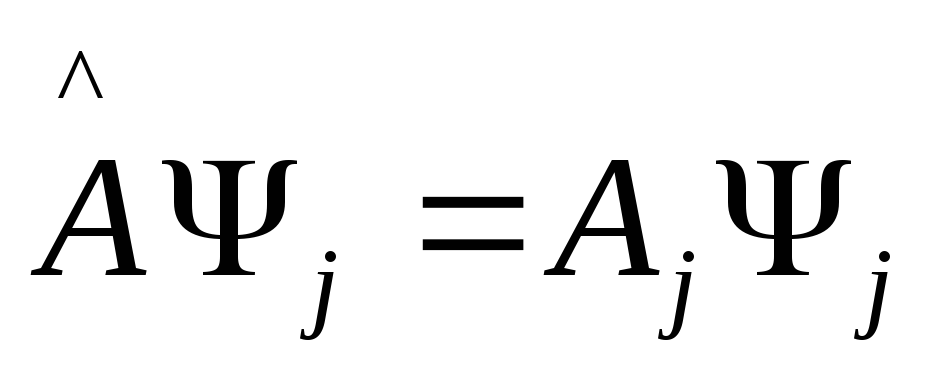
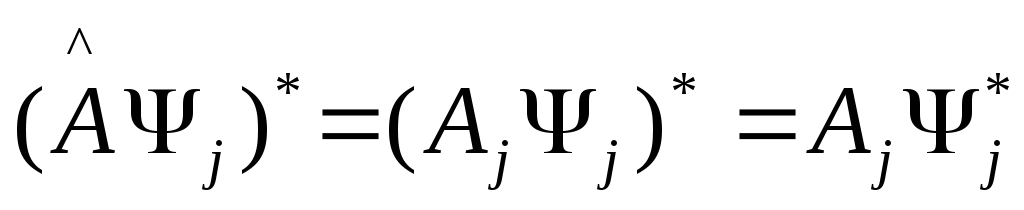(2)

Умножая (1) скалярно на слева, получим

(3)

Теперь (2) умножаем справа на , тогда

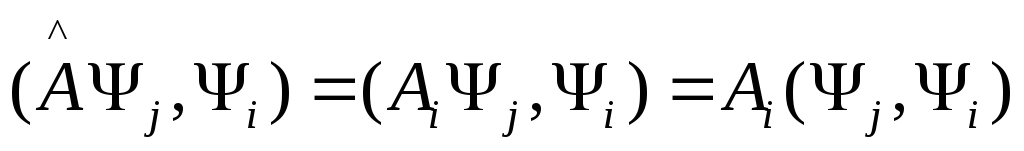(4)

Почленно из (3) – (4):

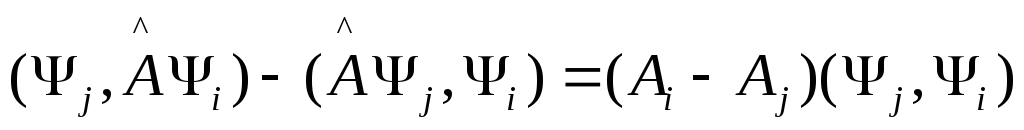(5) т.к. - эрмитов, то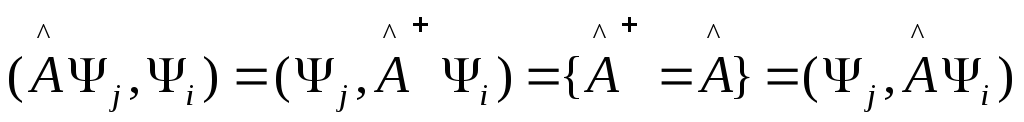. Из (5) имеем. (6)

Рассмотрим случай невырожденного спектра:

Спектр вырожденный, если одному собственному значению

соответствуют несколько собственных функций.

Например:

Невырожденный спектр – все собственные значения различные.

1) Рассмотрим (6) при , тогда,.

2) Теперь пусть . В этом случае скалярное произведение. Обычно вводят нормировку.

1 и 2 дает условие ортонормируемости .

Утверждается, что собственные функции эрмитового оператора с дискретным спектром образуют полную систему, т.е. обладают свойством полноты. Это верно для функций квантовой механики. Утверждение означает, что произвольную функцию можно разложить по собственным функция эрмитовова оператора как по базису.

Запишем это разложение:

, (9)

где индекс i пробегает по всем значениям, удовлетворяющим задаче (1).

Формулу (9) следует отличать от принципа суперпозиции

,

где - вес состоянияи суммирование ведется по произвольнымa=1,…,k. Заметим, что если (модель Юнга с ширмой и электроном), то.

Найдем коэффициенты из (9). Домножим скалярно (9) на, тогда имеем{из условия ортонормированности}=

, тогда из (9) получаем

, (9^/)

Далее

Из (9^/) также можно получить еще одно соотношение:

- равенство Парсеваля (условие замкнутости).

Теперь рассмотрим случай непрерывного спектра.

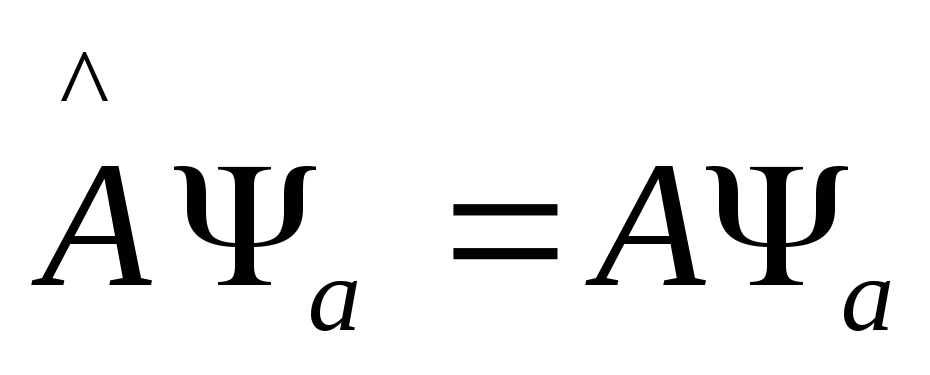- у собственной функции индексом является собственное значение. Собственные значения непрерывны, они сплошь заполняют соответствующую числовую ось.

В этом случае собственные функции не нормируемы (квадратично не интегрируемы).

Используем искусственную операцию – введем понятие собственных дифференциалов, по определению:

,

т. е. на числовой оси рассмотрим функции с равным весом на интервале .

Собственные дифференциалы (12) квадратичноинтегрируемы. Через рассмотренные собственные дифференциалы приходим к рассмотрению собственных функций.

Условие ортонормируемости: .

Здесь уже дает расходящийся интеграл, т. е. равен.

Собственные функции обладают свойством полноты, т. е. они образуют базис по которому может быть разложена любая функция:

, (13)

По аналогии с дискретным спектром:

- равенство Парсеваля