
- •Вопрос 1. Классическое и квантовое описание системы.
- •Вопрос 2 Принцип неопределенности.
- •Вопрос 4. Полный набор динамических переменных
- •Вопрос 6 Принцип суперпозиции состояний
- •Вопрос 8 Понятие о теории представлений
- •Вопрос 3. Постулаты квантовой механики.
- •Вопрос 5 Волновая функция и ее свойства.
- •Вопрос 7 Операторы в квантовой механике
- •Если , то операторы коммутативны.
- •Вопрос 10. 11. Собственные функции и собственные значения эрмитовых операторов. Случаи дискретного и непрерывного спектров.
- •Вопрос 12 Среднее значение измеряемой величины.
- •Вопрос 13 Вероятность результатов измерения
- •Вопрос 14 Коммутативность операторов и одновременная измеримость физических величин
- •Вопрос 9. Операторы координаты , импульса, момента импульса, энергии.
- •Вопрос 16 Волновое уравнение
- •Вопрос 15 Вычисление коммутаторов, содержащих операторы .
- •Вопрос 16 Волновое уравнение
- •Вопрос 23. Флуктуации физических величин.
- •Вопрос 21 Производная оператора по времени
- •Вопрос 22 Интегралы движения в кв. Механике.
- •Вопрос 24. Неравенство Гайзенберга.
- •Вопрос 17 Оператор Гамильтона различных систем.
- •Вопрос 19. Стационарное состояние различных систем
- •Вопрос 20. Решение волнового уравнения в случае свободной материальной точки
- •Для трехмерного случая
- •Вопрос 26. Собственный механический момент (спин).
- •Вопрос 27. Спиновая переменная волновой функции
- •Вопрос 29. Принцип тождественности.
- •Вопрос 28. Оператор перестановки и его свойства
- •Вопрос 31. Симметричное и антисимметричное состояния.
- •Вопрос 25. Стационарная теория возмущений в случае невырожденного дискретного энергетического спектра: нулевое и первое приближения.
Вопрос 19. Стационарное состояние различных систем
Задача Штурма-Лиувилля
для оператора
![]() :
:![]() (*)
(*)
Волновое уравнение:
![]() (**)
(**)
Как только поставили
в соответствие системе оператор
![]() , то можем решать волновое уравнение,
находим
, то можем решать волновое уравнение,
находим![]() , которая определяет состояние системы.
Задача Штурма-Лиувилля дает собственные
значения и собственные функции оператора
, которая определяет состояние системы.
Задача Штурма-Лиувилля дает собственные
значения и собственные функции оператора![]() .
.
Собственные функции задачи Штурма-Лиувилля и функции, являющиеся решением волнового уравнения совпадают при условии выполнения:
![]()
![]()
![]() ,
тогда
,
тогда
![]() . Это условие совместности решений (*) и
(**).
. Это условие совместности решений (*) и
(**).
Так как
![]() ,
то гамильтониан системы явно от времени
не зависит, т. е. поле стационарно (задача
стационарна) – это говорит о совместности
решений (*) и (**).
,
то гамильтониан системы явно от времени
не зависит, т. е. поле стационарно (задача
стационарна) – это говорит о совместности
решений (*) и (**).
Рассмотрим
стационарную задачу
![]() ,
тогда
,
тогда![]() не зависит от времени. Это либо:
не зависит от времени. Это либо:
Замкнутая система.
Система в стационарном внешнем поле.
Использую (*) и (**), получим
![]()
Это дифференциальное уравнение имеет решение
![]()
Подставим эту функцию в (*), тогда
![]() .
.
Тогда получим
![]()
Получили стационарное уравнение Шредингера.
Вопрос 20. Решение волнового уравнения в случае свободной материальной точки
Для свободной
материальной точки
![]() .
.![]() ,
тогда переходим к стационарному уравнению
Шредингера.
,
тогда переходим к стационарному уравнению
Шредингера.
![]()
Это трехмерная
задача
![]()
Оператор Лапласа
![]()
Оператор представим в виде суммы трех независимых операторов, которые коммутируют. В этом случае можно разделить переменные.
![]()
Тогда стационарное уравнение Шредингера запишется в виде
![]() ,
где
,
где
![]()
Для
![]() имеем
имеем![]() .Обозначим
.Обозначим![]() .
.
Тогда
![]() Решение этого уравнения
Решение этого уравнения![]()
Так как частица свободная, то импульс этой частицы сохраняется. Значит сохраняется направление движения частицы.
Мы выбираем движение
частицы по направлению оси x.
Тогда в силу сохранения импульса имеем
![]() .
.
![]()
Для трехмерного случая
![]()
![]()
![]()
Полная волновая функция
![]() (***)
(***)
Рассмотрим теперь коммутатор
![]()
Так как импульс
коммутирует с
![]() и не зависит явно от времени, тогда
и не зависит явно от времени, тогда![]() .
Из этого следует:
.
Из этого следует:
 -интеграл
движения.
-интеграл
движения.Собственная функция оператора импульса является решением волнового уравнения.
![]()
Найдем собственные значения оператора импульса.
![]() {используем,
что
{используем,
что
![]() ,
т. е.
,
т. е.![]() }
==
}
==![]() .
.
Тогда собственное
значение оператора
![]() :
:
![]()
Это первое дебройлевское соотношение.
Из (***) вводится
![]() - второе дебройлевское соотношение.
- второе дебройлевское соотношение.![]()
Используем, что
![]()
Уравнение (***) удовлетворяет собственной функции оператора импульса.
Вопрос 26. Собственный механический момент (спин).
Рассмотрим Na. У него есть желтая линия . Возникает при переходе с уровня 3p на 3s.
![]()
Первоначально ее
длина была 5892
![]()
Было обнаружено, что эта линия расщепляется на две: дублет.
Возникла идея расщепления уровня 3p на два, тогда можно объяснить возникновение двух линий.
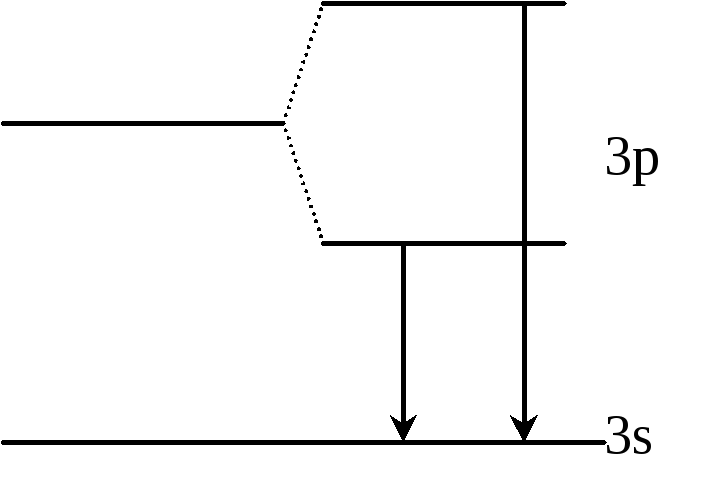
В 1925 г. Была предложена гипотеза спина, т. е. собственного механического момента.
У электрона спиновое
число s=.![]()
Впоследствии Паули ввел спин в теорию.
Если имеем одну
частицу, то она характеризуется
орбитальным квантовым числом
![]() .
.
Состовная частица
(атом) состоит из многих микрочастиц.
Можно рассматривать эту составную
частицу вцелом и приписать ей момент
![]() ,
который описывает орбитальное движение
частицы как целого.
,
который описывает орбитальное движение
частицы как целого.
Энергетический
уровень этой составной частицы в
некоторых полях будет зависеть от
орбитальных моментов микрочаститц
![]() .
.
Эти моменты являются внутренним свойством этой составной частицы.
Можно рассматривать 2 момента:
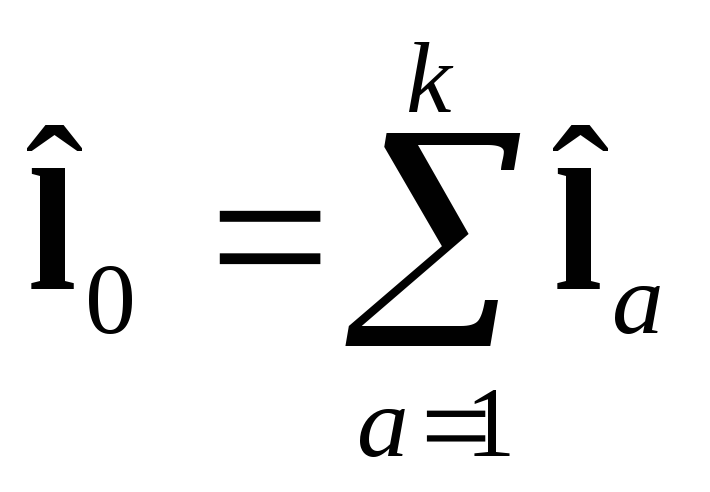 .
Этот момент описывает внутреннее
движение частицы (относительно центра
инерции)
.
Этот момент описывает внутреннее
движение частицы (относительно центра
инерции)Частица сама движется по некоторой траектории.
У частицы есть еще
квантовое число
![]() ,
характеризующее собственный механический
момент.
,
характеризующее собственный механический
момент.
Вводят оператор собственного механического момента:
![]() По
аналогии
По
аналогии
![]()
Спин – внутреннее свойство частицы. Его смысл – у частицы есть внутренний параметр, который реагирует на вращение координат независимо от места положения частицы.
