Лекции / Лекции (ЭКТ-2, Бардушкин) / Лекции в Word (2003) / Лекция 10,11

КУРС ЛЕКЦИЙ ПО ТЕОРИИ ВЕРОЯТНОСТЕЙ

Лекция № 10

Схемы независимых испытаний, служат вероятностной моделью многих реальных случайных явлений.

. Однако использовать ее при больших значениях n и m затруднительно. Поэтому приходится следить, чтобы результаты промежуточных вычислений, не выходили за диапазон допустимых значений, если такие вычисления производятся на компьютере.

Есть таблицы для вычисления , они имеют 3 входа (n, p, m), а еще хуже обстоит дело, когда требуется вычислять вероятность.

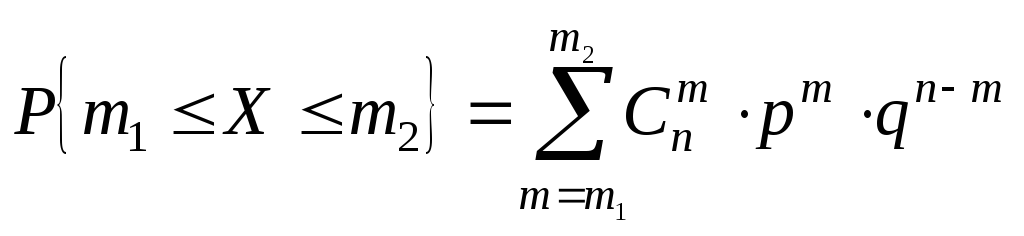, которая зависит от 4 параметров . Поэтому значительный интерес представляет задача о нахождении ассимптотических формул, которая позволяет приблизительно вычислять биномиальные вероятности.

Рассмотрим 2 теоремы (локальную и интегральную теорему Муавра-Лапласа).

§ 4. Локальная предельная теорема Муавра-Лапласа

Биномиальное распределение имеет МО равное np .

Пусть p – не близко к 0 и 1.

Теорема.

Если в схеме независимых испытаний , то для любого равномерно по всем вида , где m – неотрицательные целые числа

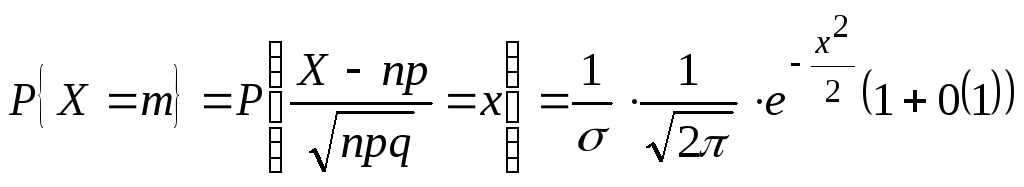
Замечание.

– затабулирована.

Эти таблицы даются, только для .

Пример.

Вероятность изделию некоторого производства оказаться бракованным равна 0,005 (p = 0,005). Чему равна вероятность того, что из n = 10000 наудачу взятых изделий, бракованных изделий окажется равно .

Решение

1) .

2)

§ 5. Интегральная предельная теорема Муавра-Лапласа

Теорема.

При равномерно по

Замечание.

– затабулирована.

Ее значения приводятся только для .

Пример.

Вероятность изделию некоторого производства оказаться бракованным равна 0,005 (p = 0,005).Чему равна вероятность, что из n = 10000 наудачу взятых изделий, бракованных окажется не более 70 (m = 70).

– ?

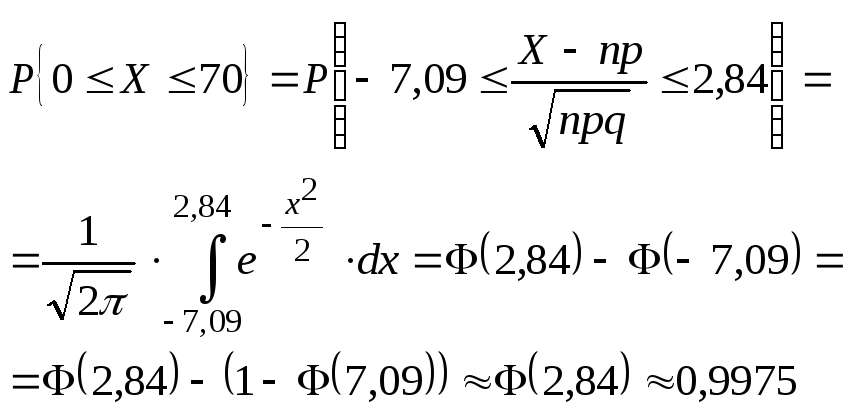
§ 6. Геометрическое распределение

Определение. СВДТ Х имеет геометрическое распределение, если ее возможные значения 0, 1, 2, …, m, …, а вероятности этих значений

Комментарий

Вероятности для последовательных значений m образуют геометрическую прогрессию с первым членом p и знаменателем q.

На практике геометрическое распределение появляется в следующих условиях. Пусть производится ряд независимых испытаний (опытов) с целью получения какого-то результата (“успеха”) А. При каждом опыте “успех” достигается с вероятностью p.

СВ Х – это число безуспешных опытов до первой попытки, в которой появляется результат А.

Ряд распределения имеет следующий вид.

X	0	1	2	…	m	…
P	p	qp	q2p	…	qmp	…

Найдем числовые характеристики СВ Х распределенной по геометрическому закону.

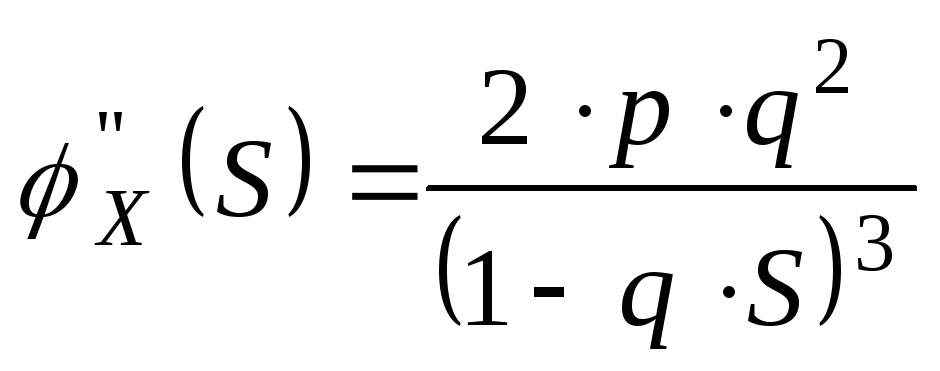
На практике чаще приходится рассматривать не СВ Х, имеющую геометрическое распределение, а .

– это число попыток до первого успеха, включая удавшуюся.

Ряд распределения

Y	1	2	…	m	…
P	p	qp	…	qm-1p	…

– геометрическое распределение, сдвинутое на 1 (геометрическое плюс 1).

Пример.

Стрелку выдаются патроны до тех пор, пока он не промахивается.

Вероятность попадания при каждом выстреле

. Какова вероятность того, что он получит не менее трех патронов.

Решение.

Пусть Х – это количество патронов, которое получит стрелок.

X	1	2	3	…
P	0,1	0,90,1	0,920,1	…

Лекция № 11

Глава VI. Некоторые важные для практики распределения непрерывных СВ

§ 1. Равномерное распределение

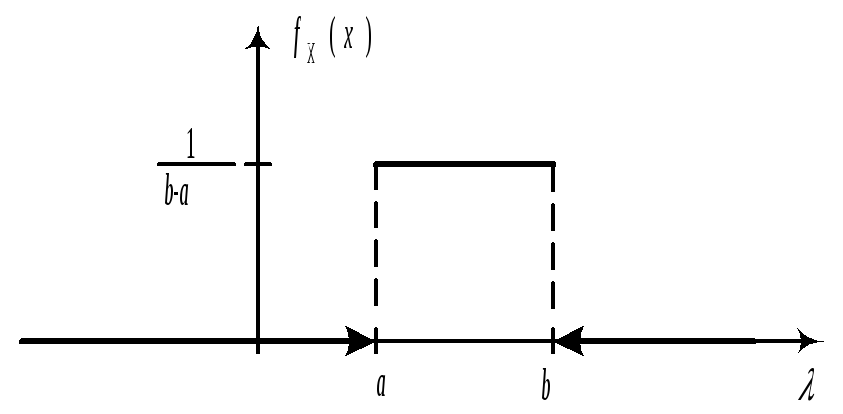
Определение. СВНТ Х называется распределенной равномерно на , если , .

Найдем константу С.

;

;

.

Пример.

Шкала измерительного прибора проградуированных в некоторых единицах. СВ Х – ошибка при округлении отсчета до ближайшего целого деления, то она будет иметь равномерное распределение на . Найдем – ?

Решение.

Замечание.

Моды равномерное распределение не имеет, а медиана совпадает с МО.

.

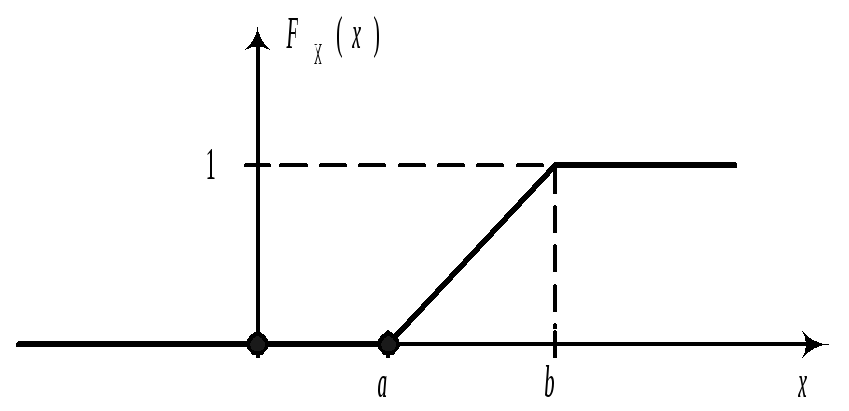
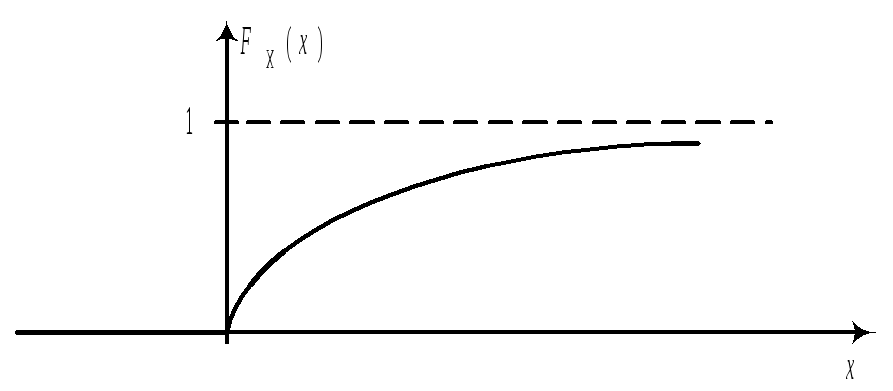
Найдем функцию распределения и построим ее график.

I Случай

.

II Случай

.

III Случай

.

§ 2. Показательное (экспоненциальное) распределе-ние

Определение. СВНТ Х называется распределенной по показательному (экспоненциальному) закону с параметром , если .

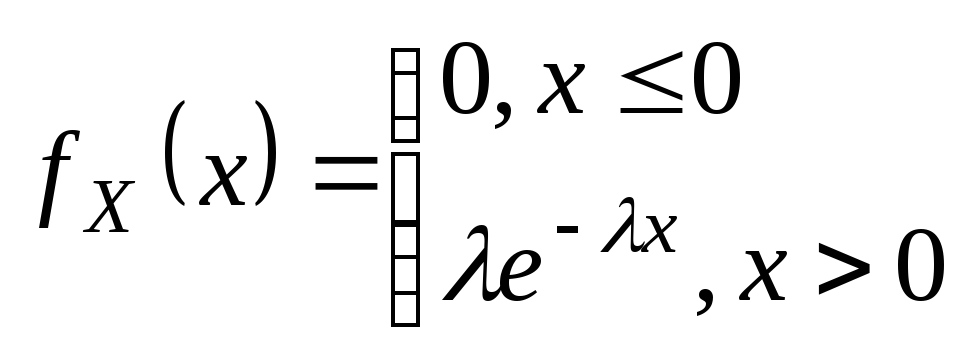Найдем – ?

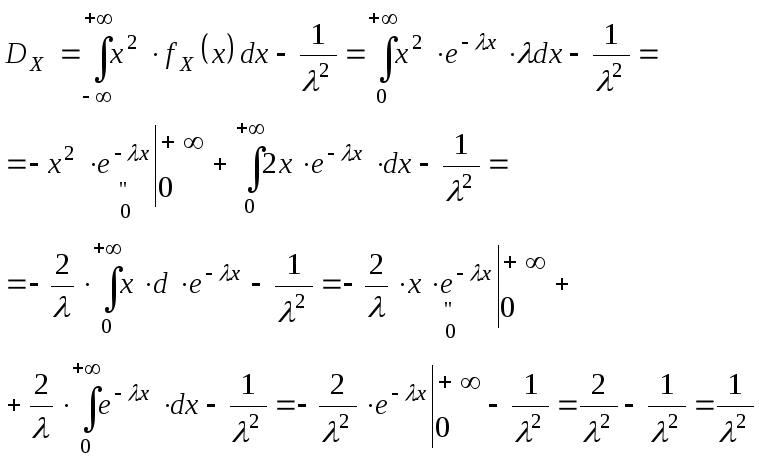
Замечание.

Среднее квадратическое отклонение для экспоненциального распределения совпадает с МО.

Найдем и построим ее график

I Случай

.

II Случай

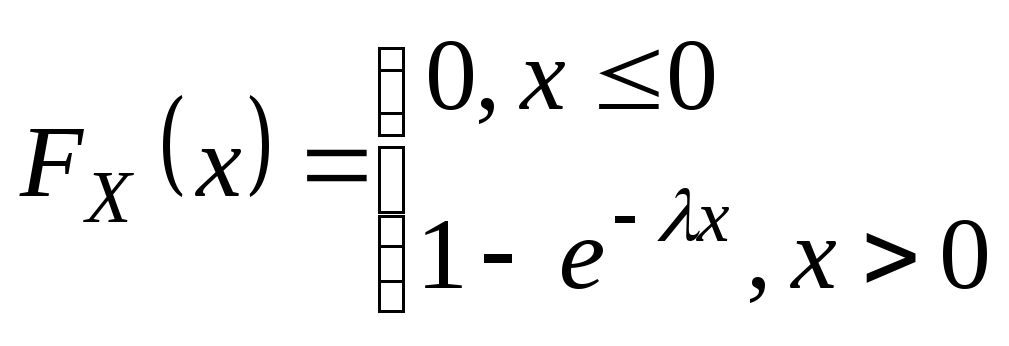
Показательное распределение тесно связано с простейшим стационарным Пуассоновским потоком событий.

Покажем, что интервал времени Т между двумя соседними событиями в простейшем потоке, имеет показательное распределение с параметром  равным интенсивности потока.

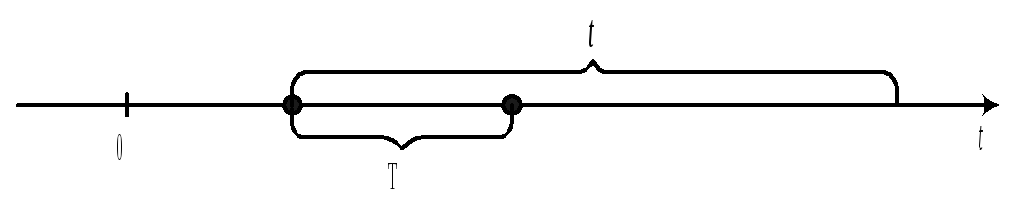
Найдем .

Для того, чтобы подсчитать эту вероятность нужно, чтобы хотя бы одно событие потока попало на участок длины t.

Продифференцировав , получим

Показательное распределение играет большую роль в Марковских случайных процессах, теории массового обслуживания и теории надежности.

Пример.

Время безотказной работы ЭВМ – это СВ Т, имеющая показательное распределение с параметром . Физический смысл  – это среднее число отказов в единицу времени, если не учитывать простоев ЭВМ. Известно, что ЭВМ уже проработало без отказов время . Найти при этом условии плотность распределения времени (время, которое ЭВМ проработает после момента , до ближайшего отказа).

Решение.

Так как простейший поток отказов не имеет последствия, то вероятность появления хотя бы одного отказа на участке (,  + t) не зависит от того, появлялись ли отказы ранее момента .

Найдем .

Вывод:

Таким образом распределение времени, оставшегося до следующего отказа, не зависит от того, сколько времени ЭВМ уже отработало без отказов.

§ 3. Нормальное распределение

Определение. СВНТ Х называется распределенной по нормальному (Гауссовскому) закону с параметрами , если плотность распределения вероятности имеет вид.

Нормальное распределение задается двумя параметрами m и .

Докажем, что – ?

Доказательство:

.

. 