Лекции / Лекции (ЭКТ-2, Бардушкин) / Лекции в Word (2003) / Лекция 13,14

КУРС ЛЕКЦИЙ ПО ТЕОРИИ ВЕРОЯТНОСТЕЙ

Лекция № 13

Y X	–1	1	Pi
0	0,1	0,06	0,16
1	0,3	0,18	0,48
2	0,2	0,16	0,36
Pj	0,6	0,4	1

Найти одномерные законы распределения компонент X и Y.

Найти вероятность того, что – ?

– ?

Решение.

X	0	1	2
P	0,16	0,48	0,36

Y X	y  –1	–1 < y  1	y > 1
x  0	0	0	0
0 < x  1	0	0,1	0,16
1 < x  2	0	0,4	0,64
x > 2	0	0,6	1

§ 3. Непрерывные двумерные СВ

Пусть A – -алгебра множеств двумерного пространства R², порожденная всевозможными прямоугольниками вида

.

Определение.

Двумерной плотностью распределения называется такая функция, что вероятность , где .

Из определения следуют ее свойства.

Свойства.

I. .

II. (условие нормировки).

III. .

IV. .

Определение.

Двумерная СВ (X; Y) называется непрерывной, если ее распределение имеет .

Пример 1:

– ?

Решение.

.

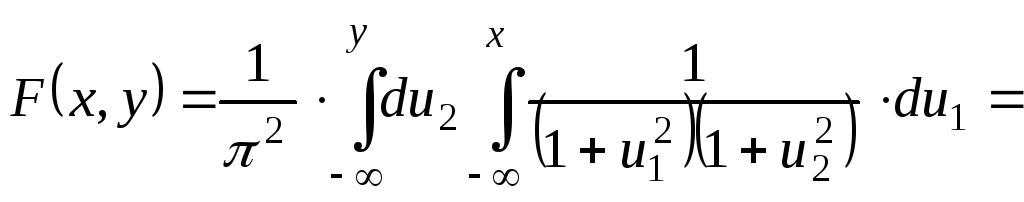
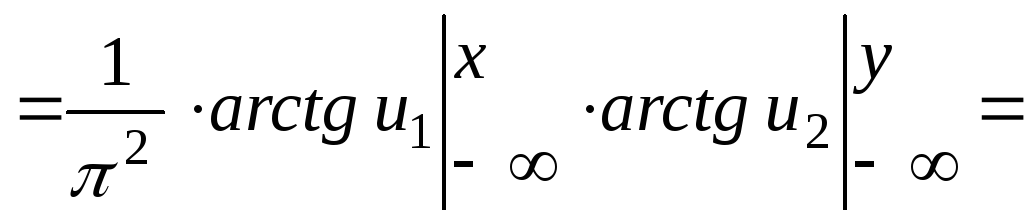
Пример 2:(двумерное равномерное распределение)

Плотность равномерного распределения на области конечной двумерной площади .

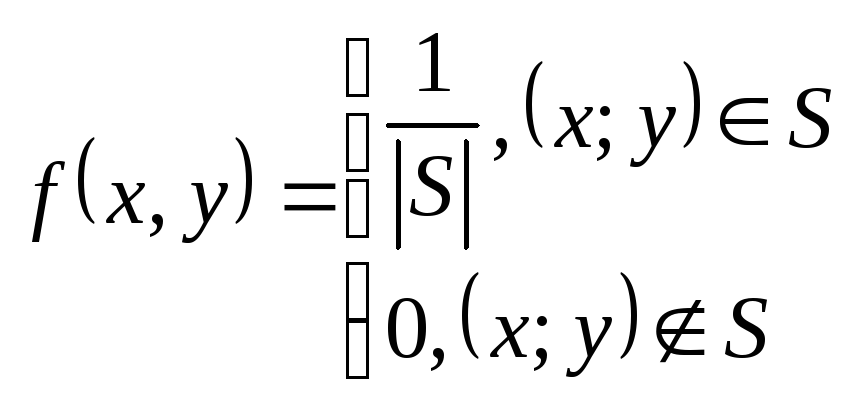
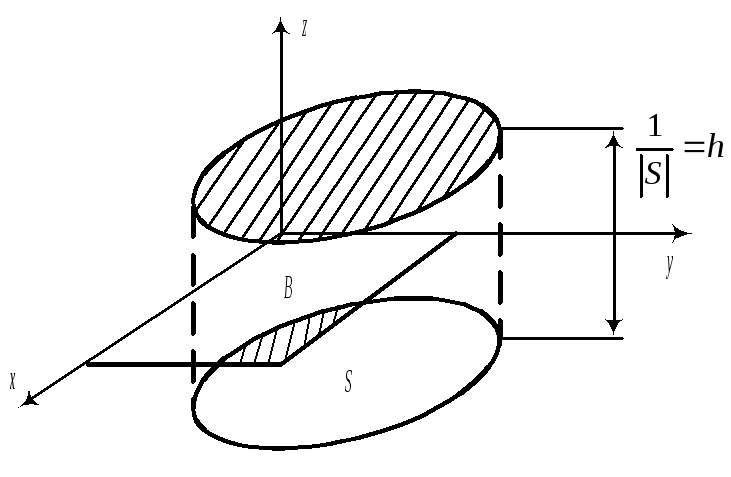
Замечание.

По последней формуле вычисляются так называемые геометрические вероятности.

Пусть известна . Найдем плотности распределения каждой из компонент X и Y.

Решение.

(*)

Продифференцируем обе части равенства (*) по Х, получим

Пример.

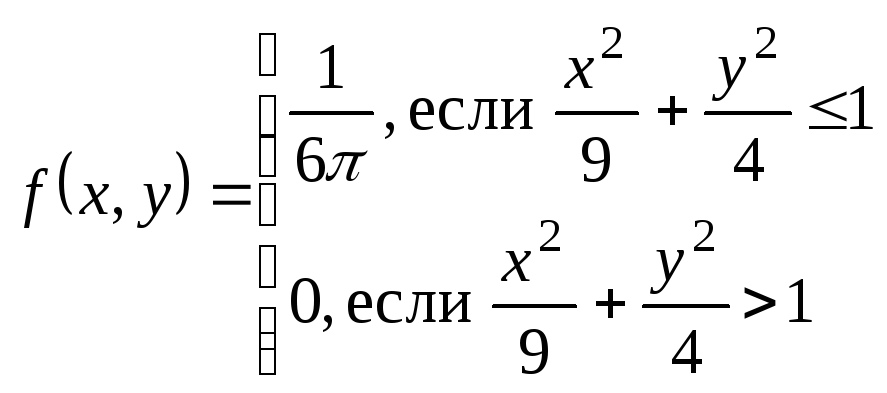
Найти:

– ? – ?

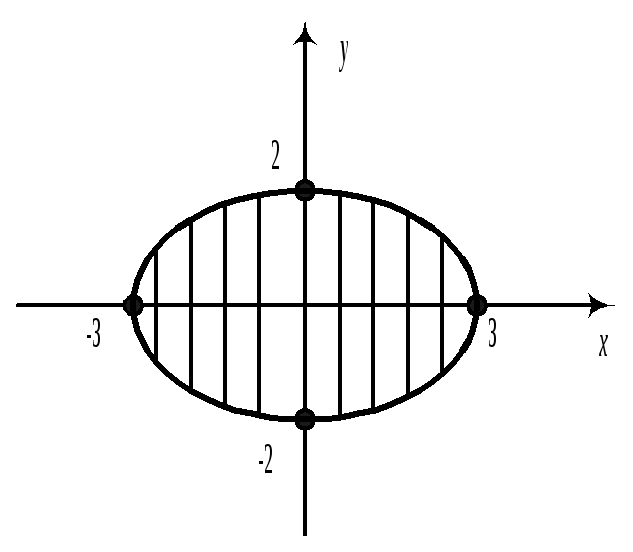
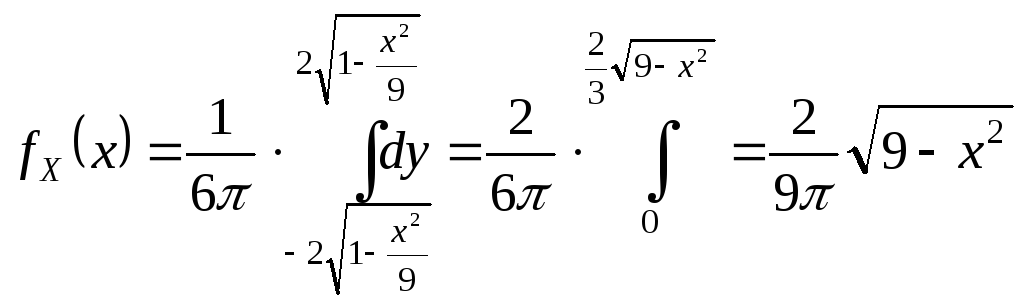
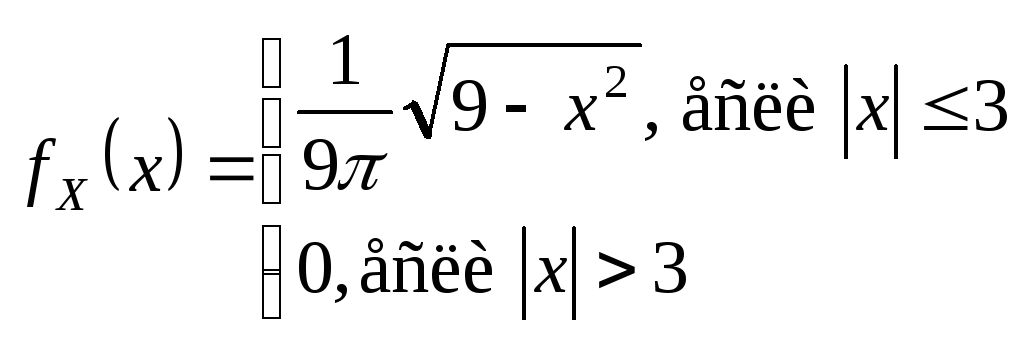
Аналогично

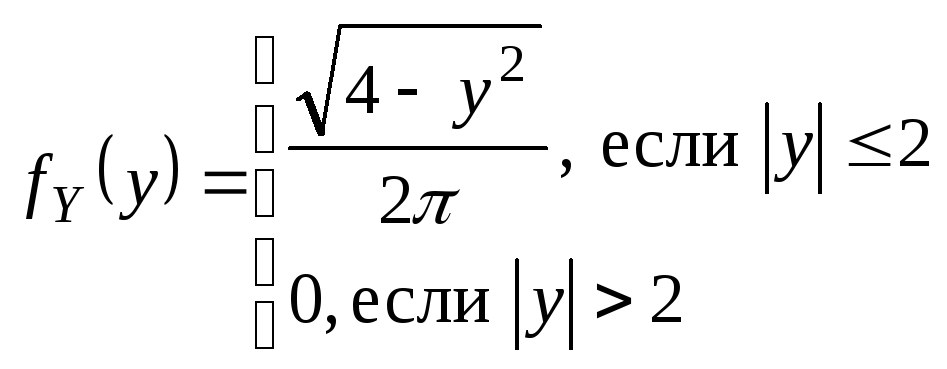
§ 4. Зависимые и независимые СВ, условные законы распределения

В двух предыдущих параграфах было показано, как зная закон распределения системы двух (дискретных или непрерывных СВ) найти законы распределения отдельных компонент X и Y.

Вопрос. Можно ли, зная законы распределения отдельных СВ (X, Y) входящих в систему , найти закон распределения всей системы? Нет, в общем виде этого сделать нельзя – это можно сделать только в одном частном случае, когда СВ X и Y образующие эту систему—независимы.

Определение.

Две СВ X и Y называются независимыми, если независимы все связанные с ними события

Замечание.

Так как зависимость и независимость событий всегда взаимны, то зависимость и независимость СВ, также всегда взаимна: если X не зависит от Y, то Y не зависит от X.

В терминах законов распределения, независимость СВ можно определить так: две СВ называются независимыми, если закон распределения каждой из них не зависит от того какое значение приняла другая.

Если компоненты X и Y двумерного вектора (X, Y) независимы, то функция распределения выражается, через функции распределения отдельных компонент.

и – независимы.

Это правило является необходимым и достаточным условием независимости для любого типа СВ.

1. Если X и Y независимые дискретные СВ с матрицей распределения .

2. Непрерывные СВ.

Лекция № 14

Пример.

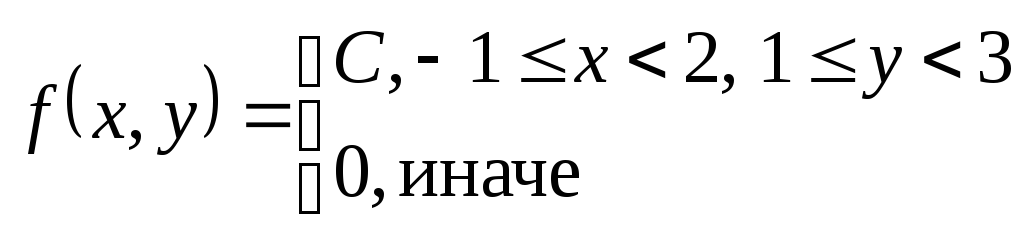
Найти:

С – ?, зависимы или независимы X и Y – ?

– ?

Решение.

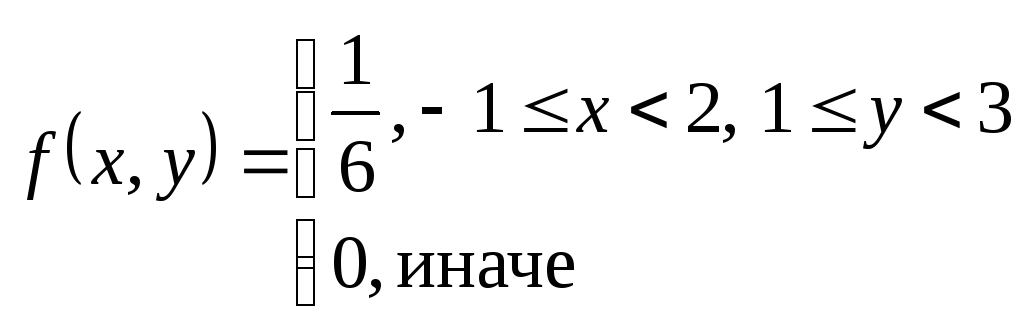
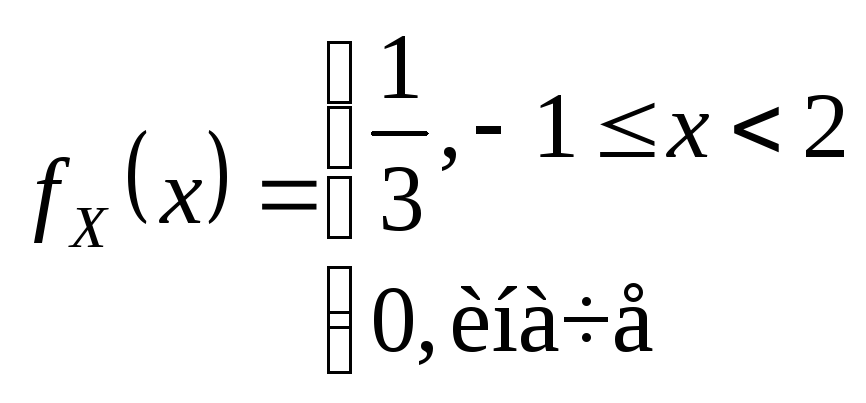
выполняется

независимы

Раз компоненты независимы, значит .

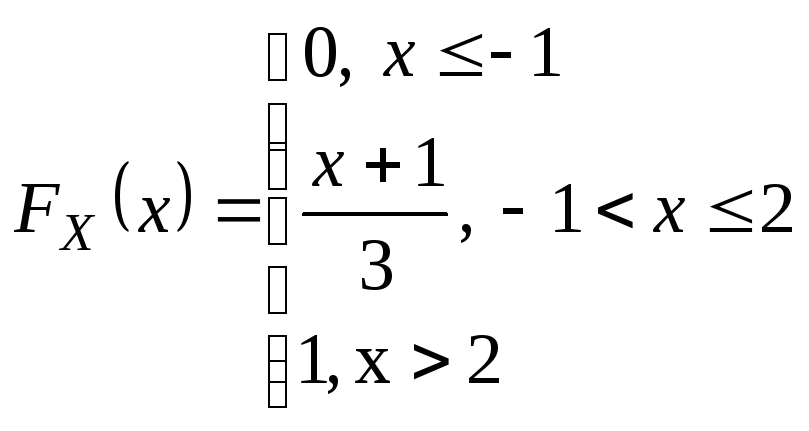
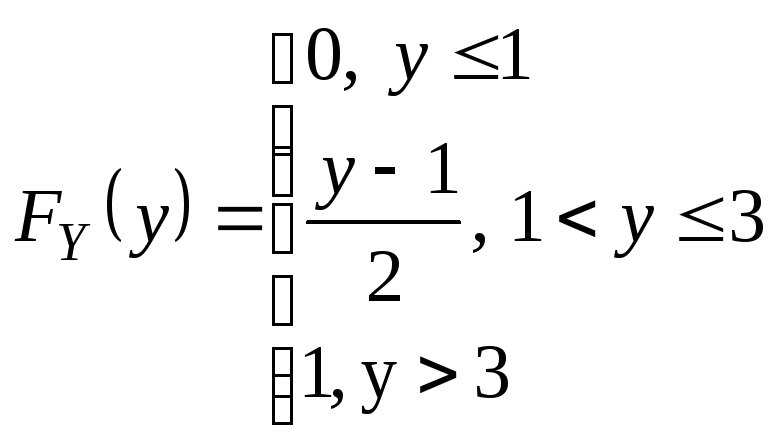
Y X	y  1	1 < y  3	y > 3
x  –1	0	0	0
–1 < x  2	0
x > 2	0		1

Если СВ образующие систему зависимы, то для нахождения закона распределения системы не достаточно знать законы распределения отдельных величин, входящих в систему, требуется знать так называемый условный закон распределения одной из них.

Определение.

Условным законом распределения одной из величин системы (X, Y) называется ее закон распределения вычисленный при условии, что другая СВ приняла определенное значение.

Начнем с наиболее простого случая, а именно со случая, когда СВ Y является дискретной.

Определение.

Условной функцией распределения называется

Замечание 1.

Условная функция распределения обладает всеми свойствами, которые присущи обычной (т.е. безусловной) функции распределения.

Замечание 2.

Если СВ X также дискретная, причем , то удобно рассматривать условную вероятность , СВ X принять значения при условии, что ,

В общем случае условную функцию распределения , однако, это не всегда возможно. Потому, что для непрерывного типа .

Чтобы отстроиться от этих неприятностей, попытаемся воспользоваться предельным переходом, заменяя событие , событием и устремив  0.

Получим.

Назовем условной функцией распределения . Оказывается такой предел всегда существует.

Если СВ Y – непрерывна, то условную функцию распределения можно определить следующим выражением

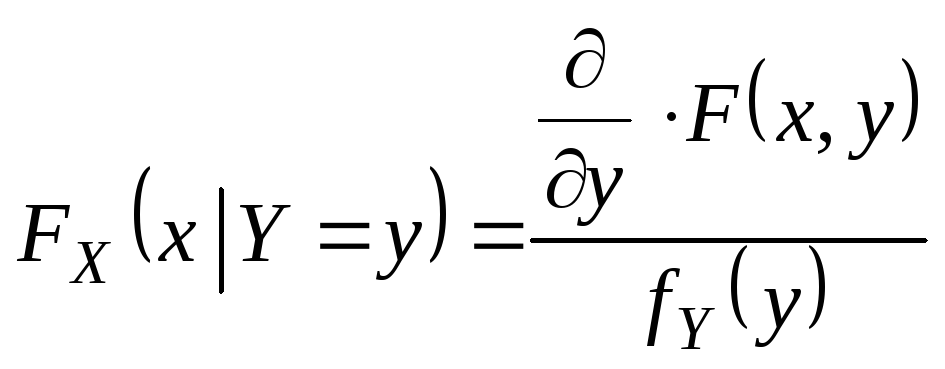
В наиболее важных для приложений случаях вектор (X, Y) представляет собой двумерную непрерывную СВ с совместной плотностью .

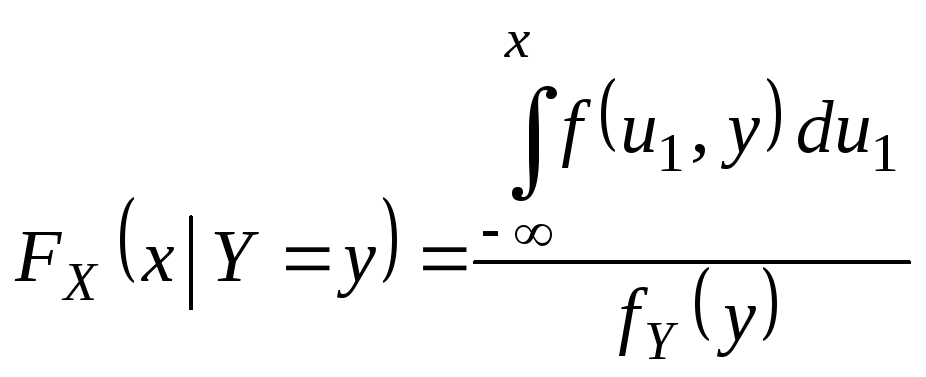
Так как функция имеет производную по x, то мы получаем окончательное выражение для условной плотности.

Пример.

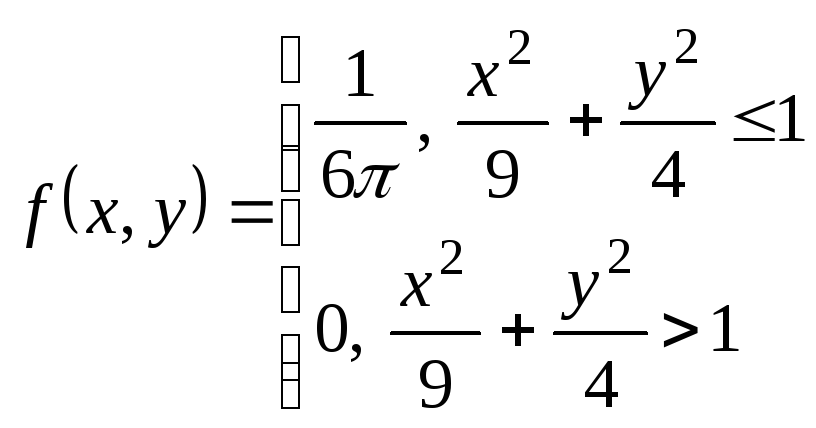
Найти:

– ?

Решение.

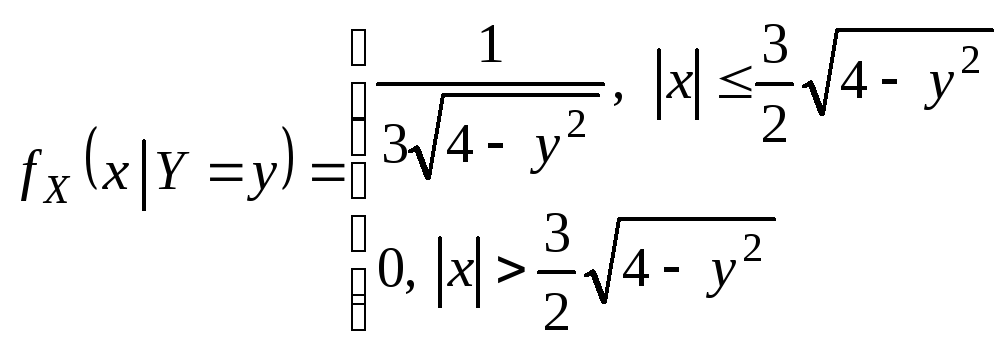
Таким образом СВ X при условии, что Y = y распределена равномерно на отрезке .

Если , то условная плотность не определена.

§ 5. Мультипликативные свойства математических ожиданий, аддитивное свойство дисперсии

Теорема.

Если СВ X и Y независимы, то .

Доказательство:

Ограничимся случаем двух дискретных СВ принимающих конечное множество значений, тогда

В силу аддитивности МО,

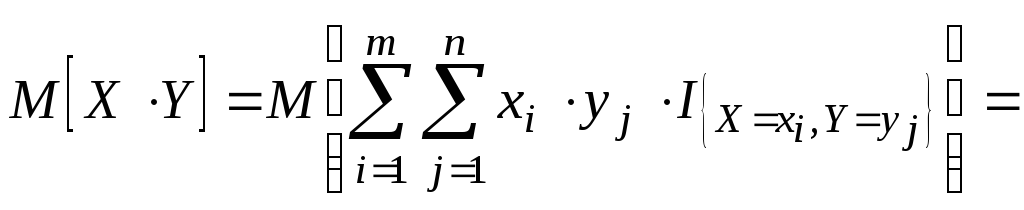
Так как СВ независимы, то

.

Следствие:

Если СВ – независимы, то (доказательство проводится методом математической индукции).

Из мультипликативного СВ МО  аддитивное свойство дисперсии.

Теорема.

Если СВ X и Y независимы, то .

Доказательство:

.

Так как X и Y независимы, то и независимы 

.

Следствие:

Если СВ – независимы, то .