
Лекции / Лекции (ЭКТ-2, Бардушкин) / Лекции в Word (2003) / Лекция 09
.docКУРС ЛЕКЦИЙ ПО ТЕОРИИ ВЕРОЯТНОСТЕЙ
Лекция № 9
Найдем важнейшие
числовые характеристики
![]() .
.
Воспользуемся производящей функцией
![]()
![]()
Возьмем производную по S.
![]()
![]()
![]()
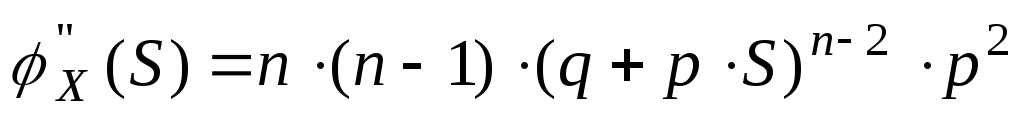
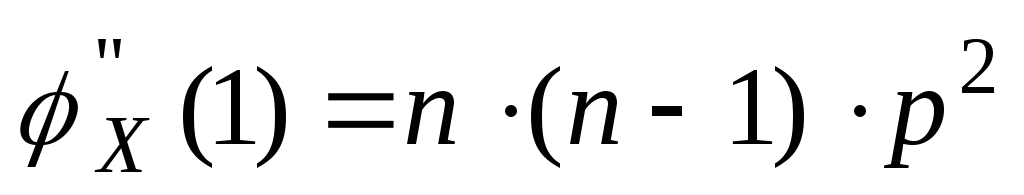
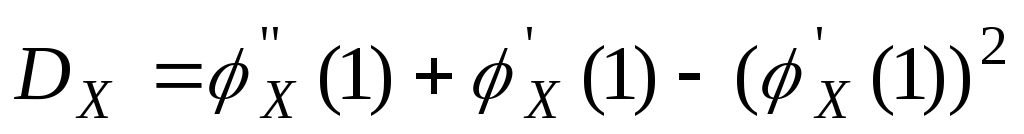
![]()
![]()
![]()
Пример.
Передается 5 сообщений по каналу связи (n = 5). Каждое сообщение с вероятностью p = 0,3, независимо от других искажается. СВ Х – количество искаженных сообщений. Построить ряд распределения, МО, DX, X, моду, а также вероятность того, что будет искажено не менее двух сообщений.
|
Y |
0 |
1 |
2 |
3 |
4 |
5 |
|
P |
|
|
|
|
|
|
|
|
0,168 |
0,36 |
0,309 |
0,133 |
0,028 |
0,002 |
![]() .
.
![]() .
.
![]() .
.
![]() .
.
![]() .
.
§ 2. Распределение Пуассона
Определение.
СВДТ Х
имеет распределение Пуассона, если ее
возможные значения 0, 1, 2, …, m,
… (счетное множество значений), а
соответствующие вероятности выражаются
формулой
![]() .
.
Замечание.
Закон Пуассона зависит только от a, смысл этого параметра состоит в следующем, он одновременно является МО и дисперсией СВ Х.
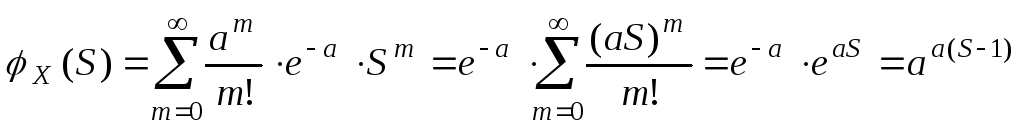
![]()
![]()
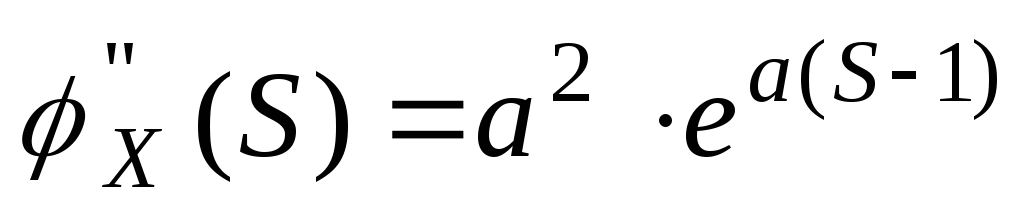
![]()
![]()
![]()
Рассмотрим условия, при которых возникает Пуассоновское распределение. Покажем, что оно является предельным, для биноминального распределения при n и одновременно р0, но nра (а~0,1–10).
Теорема (Пуассона).
Если n, р0, но npа, то фиксированного значения m, где m=0,1,…
![]() .
.
Доказательство.
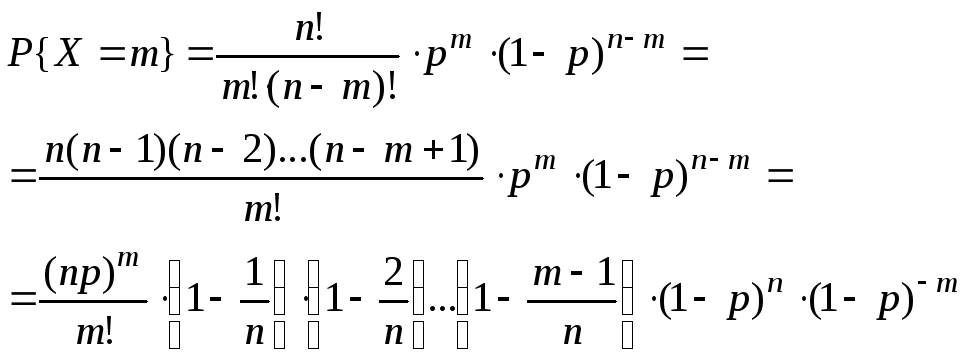
фиксированного значения m.
![]()
![]()
![]() .
.
Комментарии:
Так как n-велико, а вероятность p - очень мала, то в каждом отдельном опыте “успех” приходит редко.
Поэтому закон Пуассона в литературе называется законом редких явлений.
Пример.
Завод отправил на базу n=5000 доброкачественных изделий. Вероятность того, что в пути изделие повредится p=0,0002. Найти вероятность того, что на базу прибудут 3 негодных изделия.
Решение.
n=5000.
p=0,0002.
![]()
![]()
Имеются специальные
таблицы, с помощью которых можно найти
![]() .
.
§ 3. Простейший Пуассоновский поток
На практике часто встречаются ситуации, где имеет место распределение Пуассона.
Задача.
Пусть на оси времени 0t случайным образом возникают точки моменты появления каких-то однородных событий. (Например, вызовы на телефонной станции, приход посетителей в магазин и т.д.)). Последовательность таких моментов назовем потоком событий.
Предположим, что поток обладает следующими свойствами.
Свойства.
-
Стационарность.
Это свойство означает, что вероятность попадания, того или иного числа событий, на участок времени длиной не зависит от того, где на оси 0t расположен этот участок, а зависит только от его длины .
Из этого следует, что среднее число событий, появляющееся в единицу () времени , постоянно.
– интенсивность потока.
-
Ординарность.
Это свойство заключается в том, что вероятность попадания на малый участок t двух или более событий пренебрежимо мала с вероятностью попадания на него одного события.
Т.е. при t0 вероятность двух или более событий является бесконечно малой более высокого порядка малости, чем вероятность попадания на него одного события.
-
Отсутствие последствия.
Это свойство означает, что вероятность попадания некоторого числа событий на заданный участок оси 0t не зависит от того сколько событий попало на любой другой не пересекающийся с ним участок (в частности “будущее” потока не зависит от его “прошлого”).
Определение. Поток событий, обладающий этими 3-мя свойствами называется простейшим (или стационарным) Пуассоновским потоком.
Покажем, как простейший Пуассоновский поток связан с распределением Пуассона.

СВ Х – количество событий, попадающих на участок 0t, длиной .
Покажем, что Х имеет распределение Пуассона.
Доказательство:
Разделим участок
длины
на n
равных частей
![]() .
.
МО числа событий,
попадающих на элементарный участок t,
равно
![]() .
Согласно свойству 2 (ординарности) можно
пренебречь вероятностью попадания на
элементарный участок t,
двух или более событий.
.
Согласно свойству 2 (ординарности) можно
пренебречь вероятностью попадания на
элементарный участок t,
двух или более событий.
Назовем элементарный участок t – занятым, если на нем появилось событие из потока.
Назовем элементарный участок t – свободным, если на нем не появилось событие из потока.
A = {участок t занят}
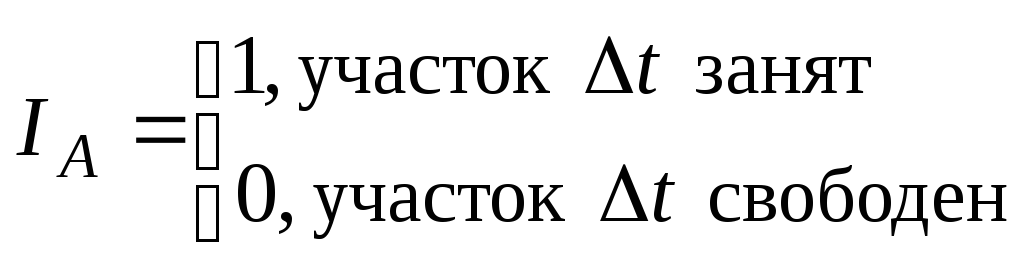
![]() – вероятность
того, что участок t
занят.
– вероятность
того, что участок t
занят.
Среднее число, то
есть МО числа событий, попадающих на
участок длины t,
будет равно
![]() .
.
![]()
![]() .
.
Рассмотрим теперь
n-участков
на временной оси, как n-независимых
испытаний (опытов), в каждом из которых
(независимость этих испытаний
из свойства 3) может появиться событие
А и
вероятность этого события
![]() .
Число занятых элементарных участков –
это и есть Х.
.
Число занятых элементарных участков –
это и есть Х.
СВ Х имеет биномиальное распределение
![]()
![]() .
.
Будем теперь
неограниченно увеличивать число
элементарных участков и найдем при
![]() .
.
Согласно теореме
Пуассона, при
![]() ,
,
![]()
![]()
Пример.
На АТС поступает простейший поток вызовов с интенсивностью =0,8 (вызовов/мин). Найти вероятность того, что за 2 минуты:
а) не придет ни одного вызова;
б) 1 вызов;
в) хотя бы 1 вызов.
Решение.
Х – количество вызовов за 2 минуты.
![]()
а)
![]() .
.
б)
![]() .
.
в)
![]() .
.
