Лекции / Лекции (ЭКТ-2, Бардушкин) / Лекции в Word (2003) / Лекция 04

КУРС ЛЕКЦИЙ ПО ТЕОРИИ ВЕРОЯТНОСТЕЙ

Лекция № 4

§ 3. Формулы Байеса

Теорема. Если – разбиение и все , тогда имеет место следующая формула:

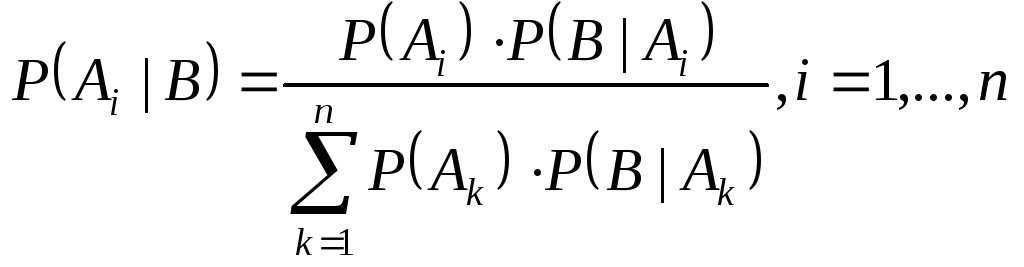
Доказательство:

По теореме умножения:

Формулы Байеса можно интерпретировать следующим образом: назовём – гипотезой, а – результат некоторого эксперимента, a – априорные вероятности, а условные вероятности – апостериорные вероятности (послеопыт-ные вероятности).

Формулы Байеса позволяют по априорным и условным вероятностям вычислить апостериорные вероятности гипотез.

Пример. Детали, изготовленные цехом завода, попадают к одному из двух контролёров для проверки на стандартность. Вероятность того, что деталь попадёт к первому контролёру – 0,6; ко второму контролёру, соответственно, – 0,4. Вероятность того, что годная деталь будет признана стандартной, для первого контролёра – 0,9; для второго – 0,98. Годная деталь была признана стандартной. Найти вероятность того, что её проверил первый контролёр.

Решение.

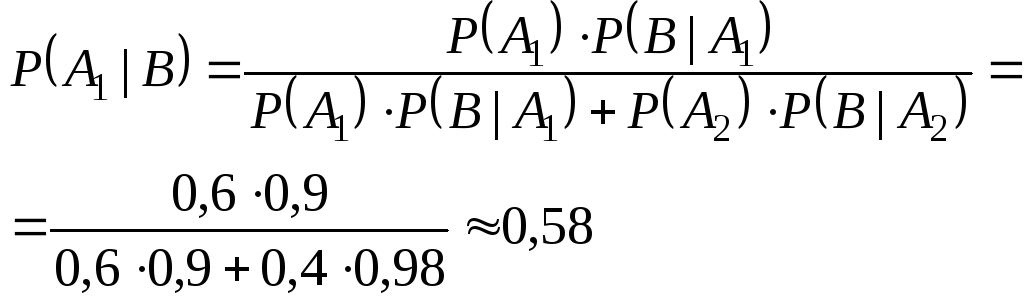
§ 4. Независимость событий

Если события A и B таковы, что

Определение. Событие A не зависит от события B, если

Если потребовать условия , то

Понятие того, что одно событие зависит от другого, симметрично.

Замечание.

Из теоремы умножения:

Это приводит к определению.

Определение. События A и B называются независимыми, если вероятность произведения событий равна произведению вероятностей событий . Если событие A не зависит от события B, то они являются просто независимыми. Если не выполняется, то события являются зависимыми.

– теоретико-вероятностная (статисти-ческая) независимость; её следует отличать от причинной независи-мости реальных явлений. Причинная независимость реальных явлений не устанавливается с помощью этого равенства, а постулируется на основе других внешних соображений. При установлении независимости событий A и B часто используется следующий принцип:

События A и B, реальные прообразы которых являются причинно-независимыми, независимы и в теоретико-вероятностном смысле. Этот принцип не является теоремой – он установлен практикой человека, а реальный смысл этого принципа можно связать со свойством устойчивости частот:

Из теоретико-вероятностной независимости не следует причинная независимость их реальных прообразов.

Пример. Из колоды в 52 карты случайно вынимается одна карта. A={туз}, B={бубновая масть}, AB={вынут туз бубновой масти}.

Решение.

События A и B – независимые события в теоретико-вероятностном смысле.

Добавим в колоду джокер:

События A и B – зависимые события в теоретико-вероятностном смысле.

Определение.

Независимость событий в совокупности.

События называются независимыми, если , где , то выполняется:

В противном случае — события зависимы.

Замечание. Из определения независимости событий в совокупности следует, что события любого подмножества множества будут независимы в совокупности.

Пример. Имеются 4 числа: 2, 3, 5, 30. Наудачу выбирается одно число. Вероятность этого события – 0,25. .

Решение.

(в совокупности зависимы).

Совокупная независимость более сильное свойство, нежели попарная независимость.

Теорема. Если события являются независимыми, индексы – все различны, вероятность , тогда:

Доказательство:

Глава III. Случайные величины и законы их распределения

§ 1. Случайные величины и законы их распределения

Пусть (Ω, A, P) – произвольное вероятностное пространство.

Определение. Числовая функция от элементарного события называется случайной величиной (СВ), если

 A (*)

Комментарий. Смысл определения состоит в следующем: поскольку не любое подмножество пространства Ω является событием, и все события составляют -алгебру подмножества A, то, естественно, рассматриваются только такие функции , для которых имеет смысл говорить о вероятности попадания в достаточно большие числовые множества. Свойство (*) гарантирует, что для любого X неравенство есть событие, а, значит, имеет смысл говорить о его вероятности.

Замечание. Если вероятностное пространство (Ω,A,P) является конечным, то случайной величиной называется любая числовая функция от элементарного события.

Определение. Множество возможных значений случайных величин X называется область значений числовой функции . Если это множество является конечным или счетным, то случайная величина называется случайной величиной дискретного типа (СВДТ). Если это множество является несчетным, то случайная величина называется случайной величиной непрерывного типа (СВНТ).

Пример 1. СВДТ. Опыт – бросание игральной кости. СВ X – число выпавших очков. Множество значений – {1, 2, 3, 4, 5, 6}.

Пример 2. СВНТ. Опыт – дважды измеряется емкость конденсатора, с помощью точных приборов. СВ X – разность между результатами первого и второго измерений.