КУРС ЛЕКЦИЙ ПО ТЕОРИИ ВЕРОЯТНОСТЕЙ

Глава I. Вероятностное пространство

Лекция № 1

§ 1. Предмет теории вероятностей

Теория вероятностей – раздел математики, изучающий закономерности случайных явлений.

Разница между закономерными и случайными событиями.

Закономерное событие – это событие, которое всегда осуществляется, как только создаются определённые условия.

Закономерное явление – это система закономерных событий.

Случайные события – это события, которые при одних и тех же условиях иногда происходят, а иногда нет.

Однако случайные события подчиняются некоторым закономерностям, которые называются вероятностными закономерностями, при этом надо условится, что мы будем иметь дело не со всякими случайными событиями, а с массовыми, то есть будем предполагать, что в принципе можно создать много раз одни и те же условия, при каждом из которых могут произойти или нет некоторые случайные события.

Пусть при осуществлении некоторых условий (N раз), случайное событие A, будет осуществляться N(А) раз.

Число N(А) – называется частотой событий A, а отношение – относительной частотой события А.

Если N велико, относительная частота для случайных массовых событий обладает свойством устойчивости.

Пример.

– серия испытаний.

– относительная частота испытаний.

  … 

Относительная частота колеблется около определенного числа, которое характеризует данное случайное событие.

Р(А) – вероятность события А.

Примеры.

1. Пусть случайное событие A – выпадение герба при одном подбрасывании симметричной однородной монеты.

Р(А) = – вероятность выпадения герба.

2. Статистика рождений показывает, что мальчиков рождается несколько больше, чем девочек. Доля рождения мальчиков 0,51-0,52.

Р(А) = 0,51; 0,51 – вероятность рождения мальчиков.

§ 2. События

Достоверное событие – событие, которое всегда происходит ().

Невозможное событие – событие, которое не происходит никогда ().

Событие – событие противоположное событию A.

происходит тогда и только тогда, когда не происходит событие A.

Суммой событий A и B называется событие A+B, которое происходит тогда и только тогда, когда происходит или A, или B, или оба вместе.

Произведением событий A и B называется событие AB, которое происходит тогда и только тогда, когда происходят A и B вместе.

Разностью событий A и B называется событие A-B, которое происходит тогда и только тогда, когда происходит A и не происходит B.

События A и B несовместны, если AB=.

Событие A влечет за собой событие B, если из наступления события A следует наступление события B (A  B).

События A и B называются равносильными A=B, если выполняются одновременно два включения

и .

Пример.

Бросается игральная кость.

A = {выпадает четное число очков}

B = {выпало число очков, не большее трех}

Решение.

Выпало число очков отличное от 5 (A+B).

Выпала 2 (AB).

Выпало число очков равное 4 или 6 (A-B).

Выпадает нечетное число очков (Ā).

Диаграммы Эйлера

В теории вероятностей очень распространенным является подход, в котором событие определяется через неопределяемые понятия элементарного события.

Наиболее употребительная теоретико-вероятностная модель – урновая модель.

Пусть имеется урна с N одинаковыми шарами. Испытание состоит в том, что из урны случайно выбирается один шар.

_n – множество шаров в урне.

Если мы из урны выбираем шар _i  A, где A – некоторое подмножество , то мы будем говорить, что произошло событие A.

Если _i  A, где A – некоторое подмножество , то мы будем говорить, что событие A не произошло.

 = {}

 – пространство элементарных событий.

 – элементарные события.

Замечания.

Операции суммы и произведения событий можно распространить на конечные и бесконечные множества событий.

,

,

В общем случае бесконечного пространства , мы будем брать не все подмножества  в отличие от конечного, а лишь некоторые классы этих подмножеств, называемые алгебрами и - алгебрами этих подмножеств.

Назовем класс A подмножеств пространств  алгеброй множеств, если

1)   A ,   A.

2) из A  A  Ā  A.

3) из A,B  A  A+B  A, AB  A.

Алгебра событий A называется -алгеброй или борелевской алгеброй, если из того, что A, n = 1,2,3,…, следует

A, A

§ 3. Вероятностное пространство

Тройка (, A, P), где

 – это пространство элементарных событий;

A – -алгебра подмножеств , называемых событиями;

P – числовая функция, определенная на событиях и называемая вероятностью.

P называется вероятностным пространством, если выполнены следующие аксиомы:

A1. P(A)  0, A  A.

A2. P() = 1 (нормированность P).

A3. P(A+B)=P(A) + P(B), если AB= (аддитивность).

A4. Для любой убывающей последовательности

событий из A такой, что

,

имеет место равенство (непрерывность P).

Замечания.

Аксиомы 3, 4 можно заменить одной аксиомой -адди-тивности.

3*. Если события A_n в последовательности A₁, A₂, … попарно несовместны, то

Из этих аксиом вытекают следующие свойства.

Свойства вероятностей

1. Если A  B, то вероятность P(B–A) = P(B) – P(A).

Доказательство:

Разобьем событие B в сумму несовместных событий

B=A+(B-A)

A(B-A)=

P(B) = P(A+(B-A))=P(A)+P(B-A) (по аксиоме 3)

P(B-A)=P(B) - P(A)  .

2. Если A  B, то P(A)  P(B)

Доказательство:

Доказательство следует из 1 свойства и аксиомы 1.

P(A) + P(B-A) = P(B)

P(B-A)  0, следовательно P(A)  P(B) .

3. A  A  0  P(A)  1

Доказательство:

A    P(A)  P()

P() = 1 (по аксиоме 2)

P(A)  0, A  A (по аксиоме 1) .

4. P(Ā) = 1 - P(A)

Доказательство:

A+ Ā = 

A Ā = 

Тогда по аксиоме 3 и аксиоме 2 получаем

P(A+ Ā) = P(),

P(A) + P(Ā) = P(),

P(A) +P(Ā) = 1  P(Ā) = 1 - P(A) .

5. P() = 0

Доказательство:

 +  = 

Тогда по аксиоме 3 и 2 получаем,

P() + P() = P()  P() + 1 = 1, P() = 0 .

6. Теорема сложения

A, B  A

P(A+B) = P(A) + P(B) – P(AB)

Доказательство:

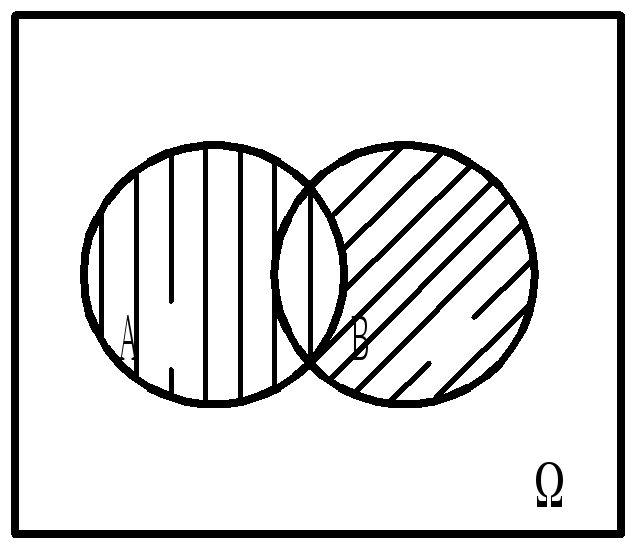
A + B = A + (B - AB), A(B - AB) = 

P(A+B) = P(A) + P(B - AB), но AB  B следовательно по первому свойству (вероятность от разности равна разности вероятностей).

P(A+B) = P(A) + P(B) – P(AB) .