Лекции / Лекции (ЭКТ-2, Бардушкин) / Лекции в Word (2003) / Лекция 05

КУРС ЛЕКЦИЙ ПО ТЕОРИИ ВЕРОЯТНОСТЕЙ

Лекция № 5

Законом распределения СВ называется любое правило (таблица, функция), позволяющее находить вероятности всевозможных событий, связанных со случайной величиной.

Если случайная величина X имеет данный закон распределения, то мы будем говорить, что она распределена по этому закону (подчинена этому закону распределения).

Наиболее простую форму можно придать закону распределения СВДТ, обычно этот закон задается рядом распределений.

Рядом распределений СВДТ Х называется таблица

X	x1	x2	…	xn	…
P	p1	p2	…	pn	…

,

Так как

– попарно несовместны, и сумма этих событий образует .

.

С помощью этой таблицы можно найти вероятности любых событий.

Пример

X	1	3	5	7
P	0,1	0,3	0,2	0,4

Часто бывает удобно иметь графическое изображение ряда распределения, так называемый многоугольник ряда распределения.

Часто удобной бывает механическая интерпретация СВДТ.

Аналитическое задание СВДТ

Примеры

1. Гипергеометрическое распределение

Это распределение числа белых шаров (X) в выборке без возвращения, объем выборки n, из урны, содержащей М – белых шаров и (N–M) – черных шаров.

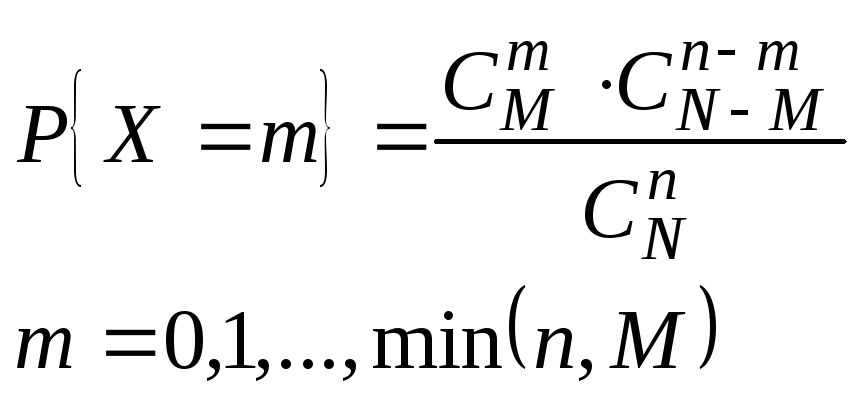
2. Равномерное распределение на множестве

§2. Функция распределения случайной величины. Её свойства. Функция распределения СВДТ.

Ряд распределения может быть построен только для СВДТ, для недискретных случайных величин из-за несчетности множества возможных значений такое представление невозможно. Наиболее общей формой закона распределения пригодной для всех типов случайных величин является функция распределения.

Функция называется функцией распределения СВ Х .

С помощью функции распределения можно выразить вероятности попадания CB Х в различные интервалы вида

Пусть , тогда разложим в сумму двух несовместных событий

тогда

(**)

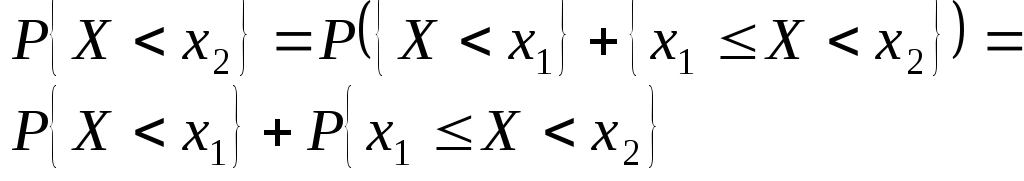
Событие можно представить, как счетную сумму несовместных событий

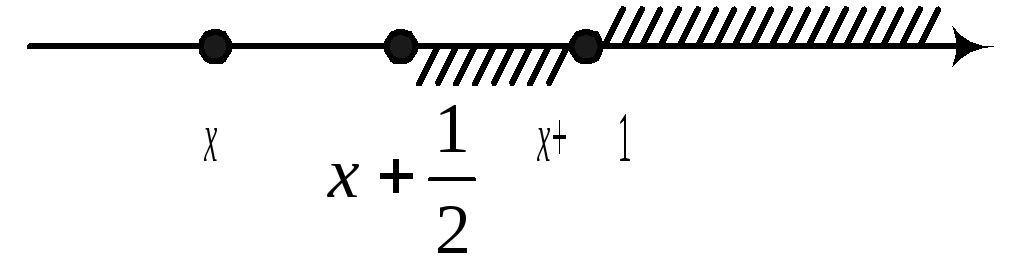
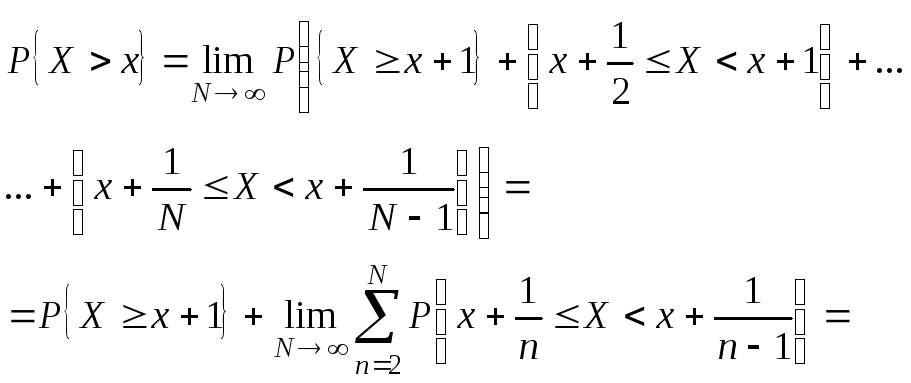
Согласно (**).

Теорема.

Функция обладает следующими свойствами:

1. – не убывает;

2. – непрерывна слева;

3. ;

4. .

Доказательство:

1. Следует из (**), т.к. .

2. Следует из аксиомы непрерывности 4, т.к. события

.

Свойства 3, 4 вытекают из аксиомы счетной аддитивности (3*), т.к. , где , тогда

Пусть

(по теореме Вейeрштрасса).

.