Лекции / Лекции (ЭКТ-2, Бардушкин) / Лекции в Word (2003) / Лекция 15

КУРС ЛЕКЦИЙ ПО ТЕОРИИ ВЕРОЯТНОСТЕЙ

Лекция № 15

§ 6. Числовые характеристики системы двух СВ. Ковариация и коэффициент корреляции

Определение.

Начальным моментом порядка системы двух СВ называется .

Если система для двух дискретных СВ, то .

Если система двух непрерывных СВ, то

.

Определение.

Центральным моментом порядка системы двух СВ называется .

а) Если система двух дискретных СВ, то

б) Если система двух непрерывных СВ, то

.

На практике чаще всего встречаются моменты I-го и II-го порядка.

Точка с координатами на плоскости OXY представляет собой характеристику положения, точек X, Y, а их разброс рассеивания происходит вокруг точек .

.

Рассмотрим отдельно.

– ковариация СВ .

Механическая интерпретация.

Когда распределение вероятностей на плоскости ХOY трактуется, как распределение единичной массы на этой плоскости, точка – центр масс распределения, дисперсии и – моменты инерции распределения или относительно точки в направлении осей OX и OY соответственно, а ковариация – центральный момент инерции распределения масс.

Теорема.

Если СВ X и Y независимы, то

Доказательство:

Для независимых СВ

, т.к. X и Y независимы.

 .

Замечание.

Попутно доказано, что в общем случае вычисляется по следующей формуле ,

Замечание.

характеризует не только степень зависимости СВ, но также их рассеявание вокруг точки центра масс, но к сожалению размерность равна произведению размерностей X и Y. Чтобы получить безразмерную величину, характеризующую только зависимость, а не разброс ковариацию делят на произведение .

Определение.

Величина называется коэффициентом корреляции СВ X и Y.

Коэффициент характеризует степень зависимости СВ X и Y, но не любой, а только линейной зависимости, которая проявляется в том, что при возрастании одной СВ X , другая также проявляет тенденцию возрастания, в этом случае .

Если одна возрастает, а другая убывает, то .

В первом случае говорят, что две СВ связаны положительной корреляцией. Во втором случае говорят, что две СВ связаны отрицательной корреляцией. Модуль характеризует степень тесноты линейной зависимости между СВ X и Y. Если линейной зависимости нет, то .

Теорема.

Если же СВ X и Y связывает жесткая функциональная линейная зависимость , то при , при .

Доказательство:

.

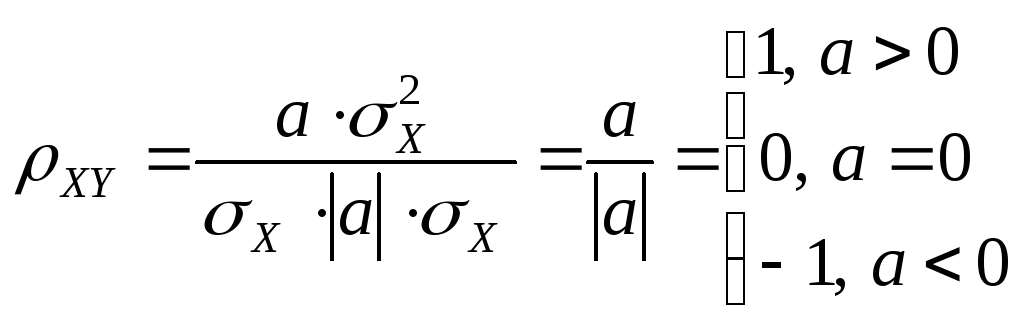Теорема.

.

Доказательство:

Рассмотрим СВ , тогда

.

Определение.

СВ X и Y называется не коррелированными, если (или ).

Замечание.

Из независимости СВ следует их не коррелированность. Обратное не верно. Из коррелированности не вытекает их независимость.

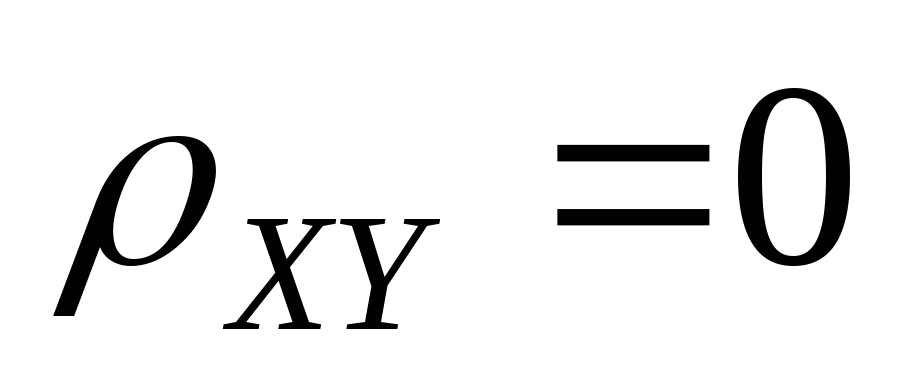
независимы			(отсутствие линейной зависимости)
			(обратное не верно)

При этом любая другая зависимость может иметь место.

Пример.

Y X	0	2	5	Pi
1	0,1	0	0,2	0,3
2	0	0,3	0	0,3
4	0,1	0,3	0	0,4
Pj	0,2	0,6	0,2	

Найти: – ?

Решение.

Очевидно, что компоненты X и Y зависимы.

,

,

, значит между компонентами X и Y существует отрицательная линейная зависимость.

Теорема.

Доказательство:

Следствие:

(доказательство проводится методом математической индукции).