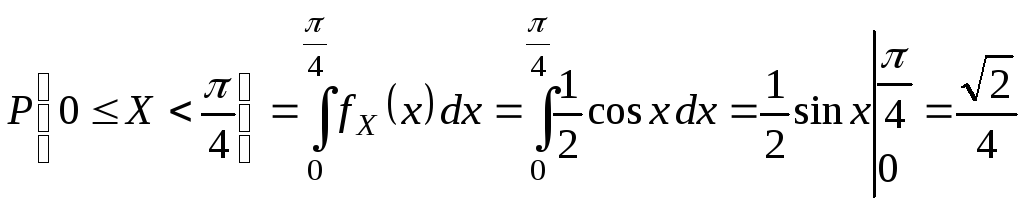Лекции / Лекции (ЭКТ-2, Бардушкин) / Лекции в Word (2003) / Лекция 06
.docКУРС ЛЕКЦИЙ ПО ТЕОРИИ ВЕРОЯТНОСТЕЙ
Лекция № 6
Из равенства
![]() следует, что в точках разрыва функции
следует, что в точках разрыва функции
![]() имеет место положительная вероятность.
имеет место положительная вероятность.![]()
Так как при каждом
натуральном n
может быть не более n-точек
x
с вероятностями
![]() ,
то у функции
,
то у функции
![]() имеется не более счетного числа точек
разрыва.
имеется не более счетного числа точек
разрыва.
Обозначим через
![]() все точки разрыва функции
все точки разрыва функции
![]() ,
если вероятности
,
если вероятности
![]() таковы, что
таковы, что
![]() ,
то это равносильно тому, что СВ X
имеет дискретное распределение, то есть
является СВДТ.
,
то это равносильно тому, что СВ X
имеет дискретное распределение, то есть
является СВДТ.
Замечание.
Для СВДТ
![]() имеет ступенчатый вид.
имеет ступенчатый вид.
Пример.
-
X
-3
-1
0
2
3
P
0,1
0,3
0,1
0,3
0,2
Получить функцию распределения и построить ее график.
Решение.
![]()
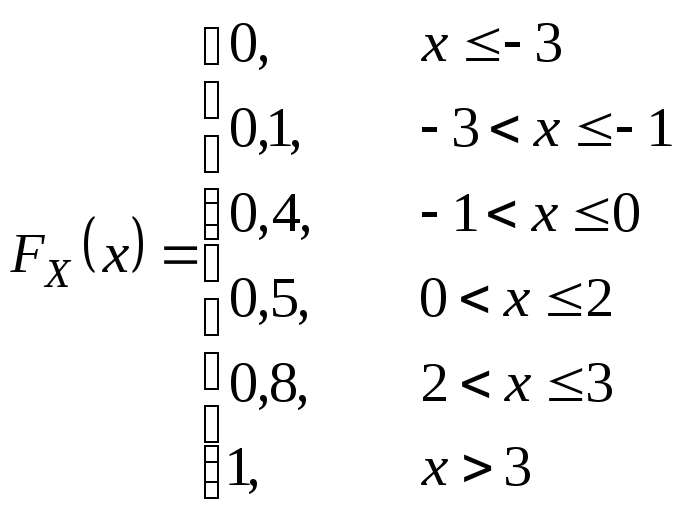
![]()
![]()
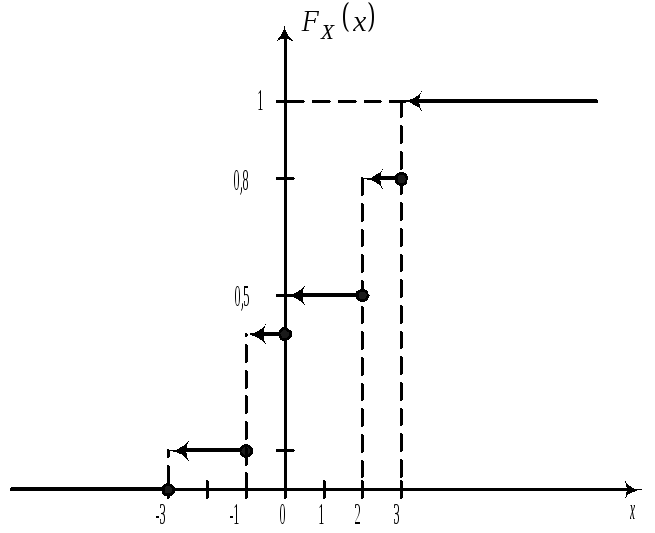
Введем новое важное понятие индикатора события.
Определение.
Индикатором события A
A
называется СВ
 .
.
Ряд распределения
случайной величины
![]() имеет следующий вид
имеет следующий вид
|
IA |
0 |
1 |
|
P |
1–p |
p |
где р-вероятность события А.
Многоугольник распределения
Функция распределения

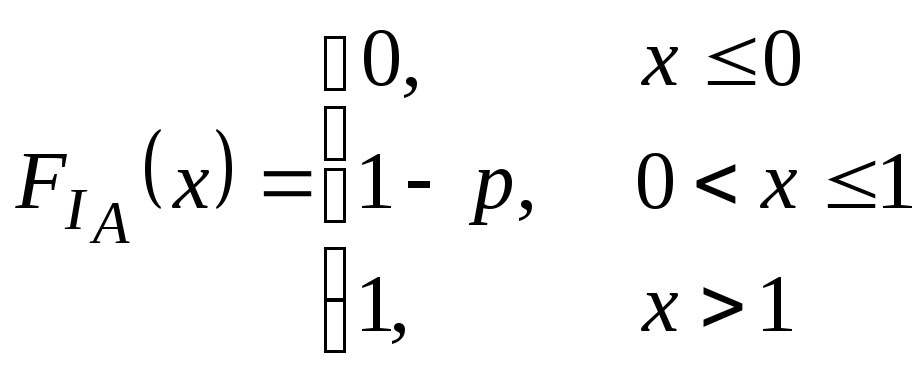
§3. Непрерывная СВ. Плотность распределения.
Определение.
Функция
![]() есть плотность распределения СВ X,
если
есть плотность распределения СВ X,
если
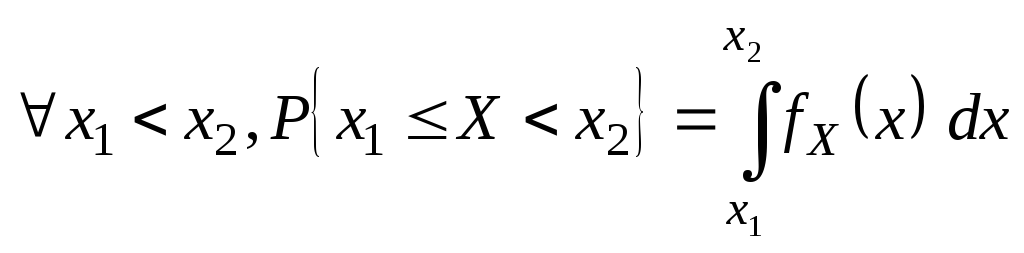 (***)
(***)
Из определения (***) следуют свойства плотности распределения.
Свойства
1.
![]()
Замечание.
Для СВ X
имеющей функции. Плотности из свойства
1 и теоремы из курса математического
анализа (о непрерывности интеграла с
переменным верхним пределом)
что
![]() непрерывна.
непрерывна.
2.
![]() в точках непрерывности
в точках непрерывности
![]() .
.
3.
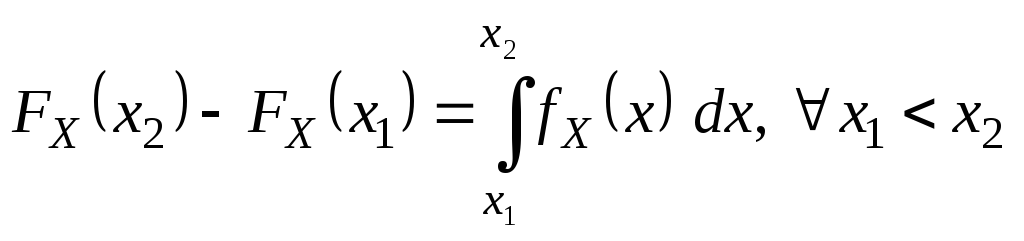 .
.
4.
![]() ,
т.к.
,
т.к.
![]() неубывающая функция, то
неубывающая функция, то
![]() .
.
5. Условия
нормировки:![]() .
.
Определение.
СВ X
называется СВНТ, если ее распределение
имеет функцию плотности
![]() .
.
Через плотность
![]() можно выразить любую вероятность
можно выразить любую вероятность
![]() .
.
Примеры.
I.
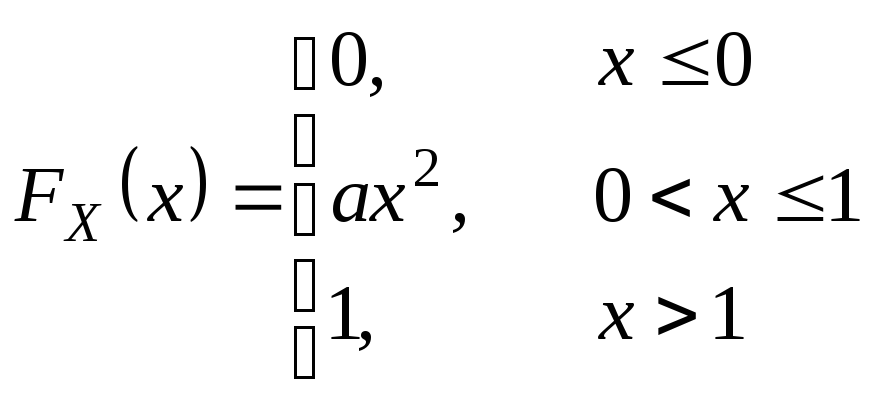
-
a – ?
-
 и построить ее
график – ?
и построить ее
график – ? -
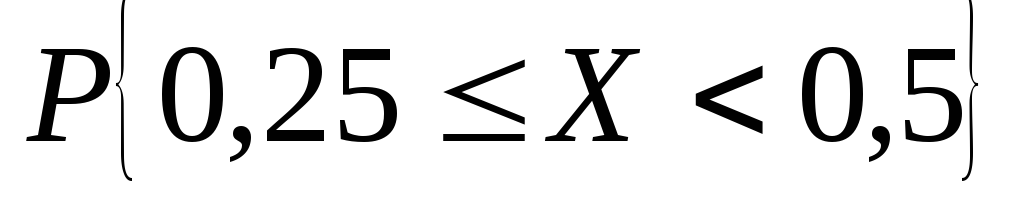
Решение.
-
Так как
 непрерывная в точке 1 и
непрерывная в точке 1 и
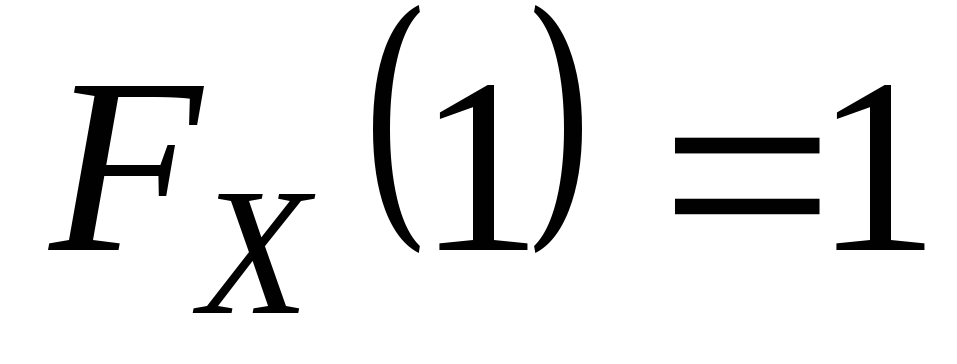 ,
то
,
то
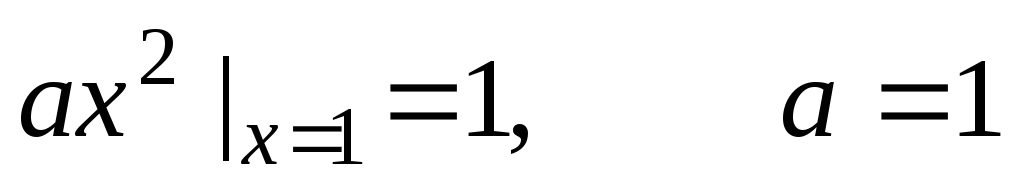 .
. -
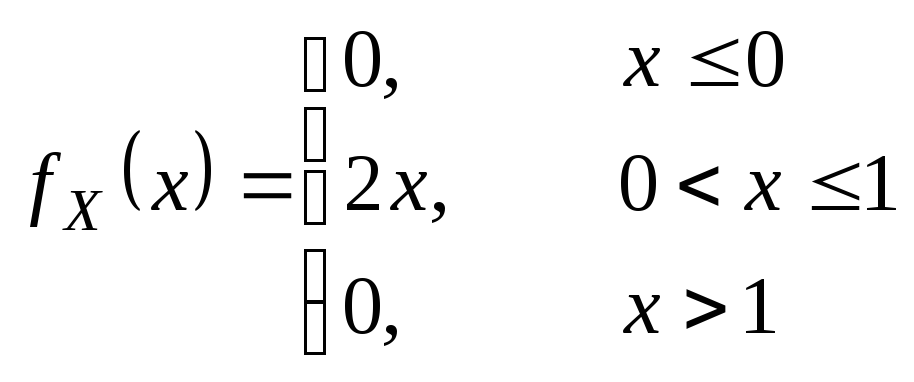

II.
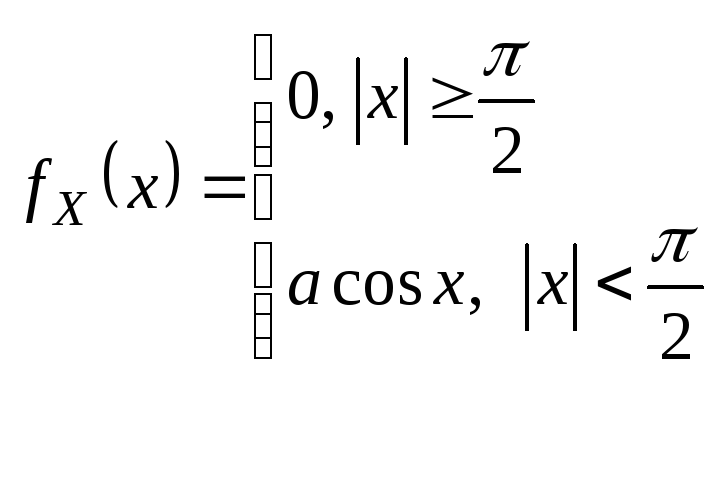
-
a – ?
-
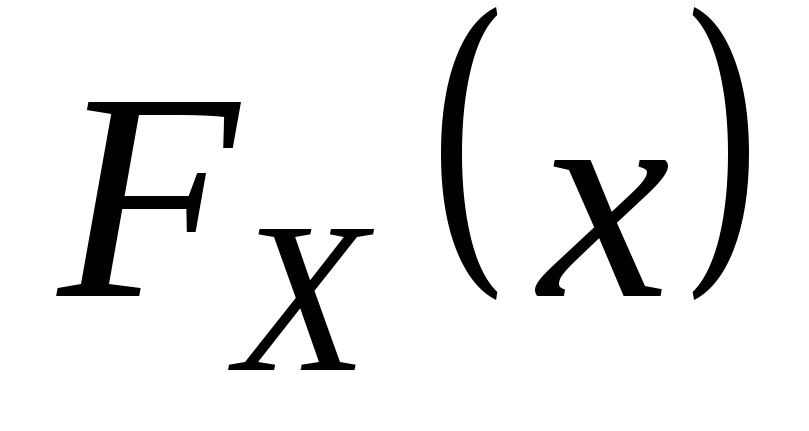 и построить ее
график – ?
и построить ее
график – ? -
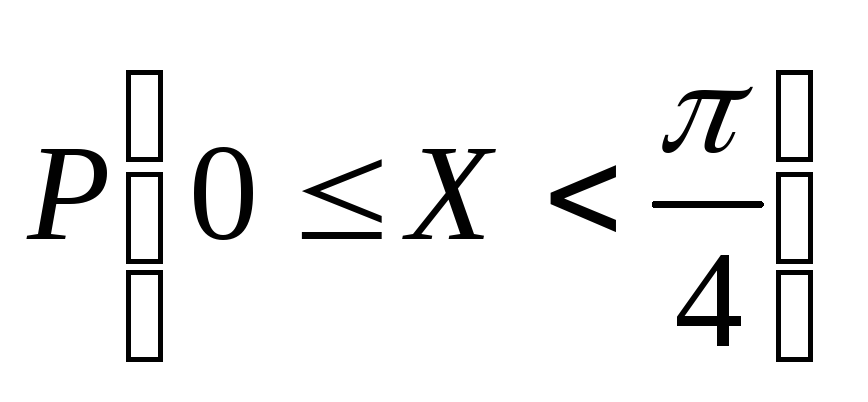 – ?.
– ?.
1)![]()
![]() .
.
2)
![]()

1.
![]()
![]()
2.
![]()

3.
![]()
![]()
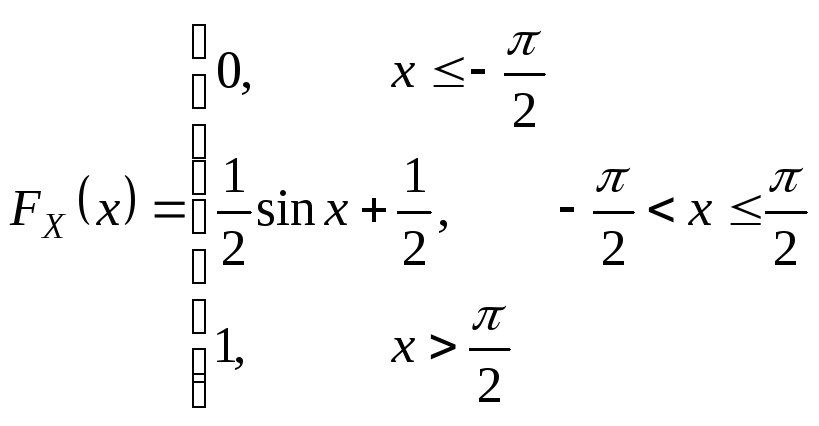
3)