Лекция 2.

§1.3. Аксиомы теории вероятности и следствия из них.

Вероятность строится как некая числовая мера.

Определение: система подмножеств из Ω (F), удовлетворяет условиям:

1. Ω  F (Ω элемент этой системы F);

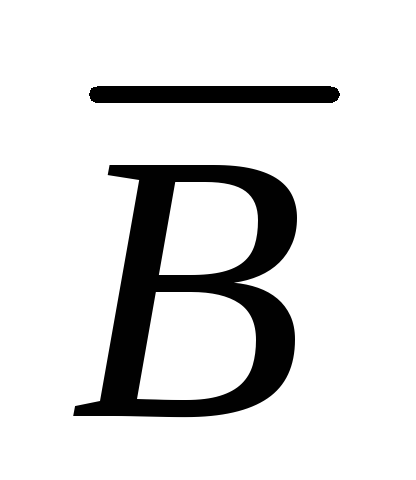
2. A, B  F => A+B  F, AB  F, и F, называется алгеброй.

Если условие 2 выполняется для счетного числа событий, то такая система называется - алгеброй.

Определение: наблюдаемое событие называется такое подмножество из Ω, которое одновременно является элементом из F.

Поле событий является алгеброй.

Определение: вероятностью события A называется числовая функция P(A), определяется на алгебре событий F и такая, что выполняется следующие 3 аксиомы:

Аксиома 1. P(A)≥ 0. Аксиома 2. P(Ω)=1 (вероятность достоверного события).

Аксиома 3. Для любых A₁, A₂, A₃,….. A_n, таких что A_iA_j=0, i≠j (попарно несовместных) выполняется:

P(A₁+A₂+…..+A_n)=P(A₁)+P_P(_n).

Замечание: если аксиома 3 выполняется для счетного числа событий, то она называется аксиомой  - аддитивности.

Следствия из аксиом

Аксиомы вводят свойства числовой функции вероятности. Формализация модели равносильна построению вероятностного пространства {Ω , F, P}.

Система аксиом хоть и не противоречива, но она и не полна.

1. P()=0 (вероятность невозможного события = 0) невозможное событие обязательно принадлежит алгебре)

Доказательство:  + Ω = Ω  сумма несовместимых  (по аксиоме 2,3) P()=0.

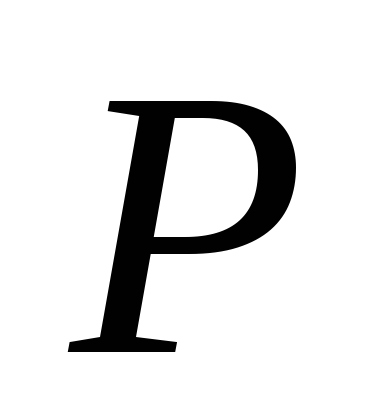2. (A)=1-P()

Доказательство: A+=Ω (закон исключенного третьего)  (по аксиоме 2,3) P(A)=1-P()

3) Если  B  P(A) ≤ P(B)

Доказательство: представим В более широким событием В=ВΩ=В(А+)=ВА+В. Но так как АВ=А (по закону поглощения), то В=А+В - сумма двух несовместимых событий по аксиоме 3  Р(А)=Р(В) ≥ 0 Р(А) ≤ Р(В)

4) P(A) ≤ 1

Доказательство: действительно, А  Ω  (из следствия три), что свойство доказано.

5) Формула сложения вероятностей.

Для  А,В: Р(А+В)=Р(А)+Р(В)-Р(АВ) (2)

Доказательство:

A+B=(A+B)Ω = (А+В)(А+)=A+A+AB+B=A+AB+B=A+B=>P(A+B)=P(A)+P(B) (3)

По формуле (1): B=AB+B  (по аксиоме 3) P(B)=P(AB)+P(B). Подставим в формулу (3)

Р(В)=P(B)-P(AB)  P(A+B)=P(A)+P(B)-P(AB)

В частном случае, когда А,В - несовместны  P(AB)=0  аксиома аддитивности.

6) Формула сложения для 3-х событий.

P(A+B+C)=P((A+B)+C)=P(A+B)+P(C)-P((A+B)C)-P(A)+P(B)-P(AB)+P(C)-(P(AC)+P(BC)-

-P(ABC))=P(A)+P(B)+P(C)-P(AB)-P(BC)-P(AC)+P(ABC)

P(A+B+C)=P(A)+P(B)+P(C)-P(AB)-P(BC)-P(AC)+P(ABC) (4)

7) Для  А₁, А₂,….,А_n : (5)

Задача (о рассеянной секретарше): Дано n писем и n конвертов секретарша все перепутала. Получит ли хотя бы один из адресов свое письмо?

8) Формула классической вероятности.

Пусть выполнены два условия:

1. Ω =₁, ₂,…, _n - конечное,

2. P(₁)=P(₂)=…= P(_n) – равновероятны.

Тогда справедлива формула:

, где - число элементовА, - число элементовΩ.

Причем А =_k1, _k2,…, _km Ω и

Доказательство: Т.к. Ω =₁+₂+…+_n => (по аксиоме 2,3) 1=Р(₁)+Р(₂)+Р(_n)=рn, где p=p(_k), k=1,2,..,n  p=1/n P(A)=mn=.

Пример 1. Из колоды в 36 карт наудачу извлекаем одну карту. Найти вероятность события С=появится картинка или карта красной масти.

Решение: логика => Алгебра => правила исчисления вероятности сложных событий. Ключевым является слово “или” => C=A+B, где А=появится картинка, В=появится карта красной масти.

По Ф.С.В.(2) => P(C)=P(A)+P(B)-P(AB)=.