Лекция 13.

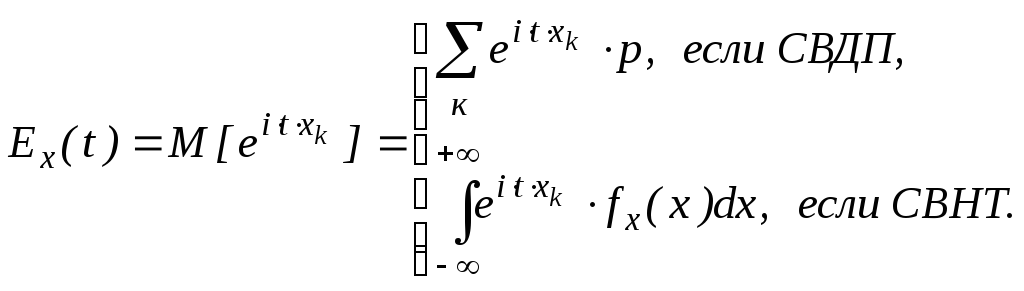(1)

Пример 1. Пусть X~P_u(). Вычислить характеристическую функцию E_x(t).

Решение.

По формуле (1) 

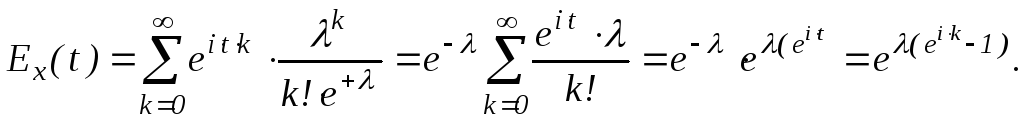
X~P_u()=E_x(t)=

Свойства характеристической.

1. E_x(t) – существует для любых распределений, причем E_x(t) ≤ 1, E_x(t)=1.

Доказательство.

Для определенности пусть Х~СВНТ  E_x(t)=. Оценим по модулю.

, .

2. Пусть Y=aX+b  E_y(t)=

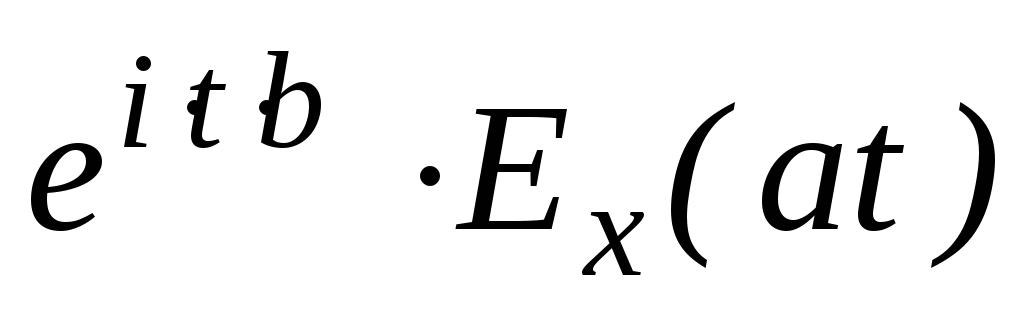
Доказательство.

3) Пусть Y=X₁+ X₂+…+ X_n ,где X₁, X₂,…, X_n – независимы в совокупности 



Доказательство.

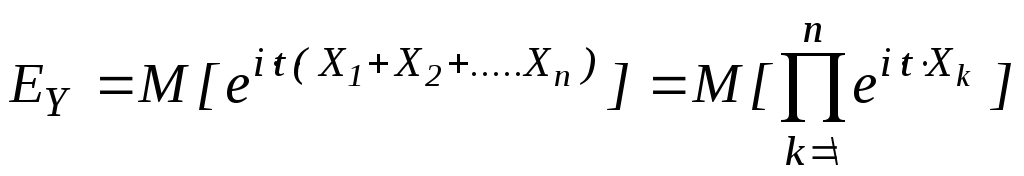=(обобщение теоремы 11.2. на формулу вектора) = = (в силу независимости) =

4)……… величины Х до n-го порядка включительно ( т.е.  , к=1,2,…,n , причем

Доказательство.

Для определенности рассматриваем СВНТ.

(2)

Проверим абсолютную сходимость интеграла:

- существует по условию 

• 

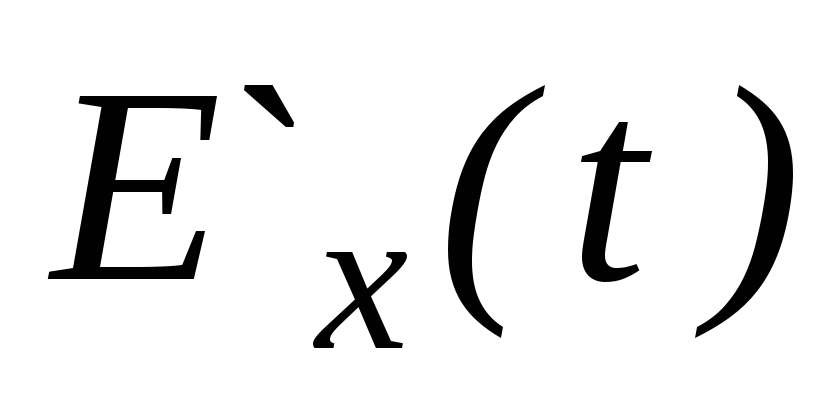
Из (2)  =

Продолжая дифференцирование под знаком интеграла, получим результат.

Пример 2. X~N(0,1). Вычислить Е_x(t).

Решение.

 (по свойству 4.) 

= (возьмем интеграл по частям) = =



,

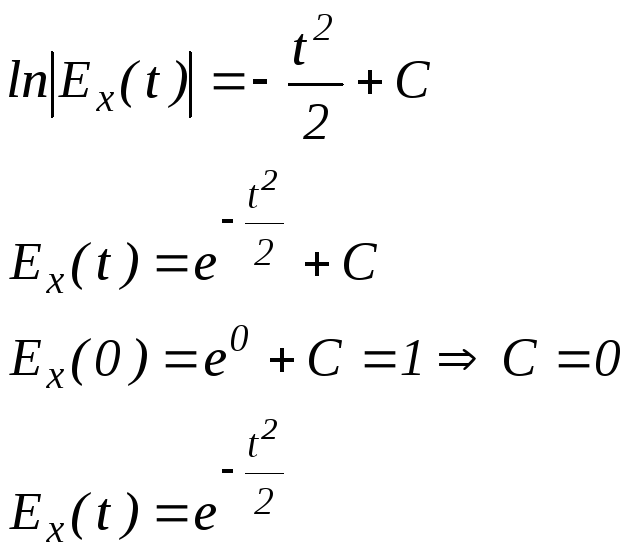
5) Применим операцию комплексного сопряжения, тогда:

Доказательство.

=

=

Следствие из свойства 5.

а) Если характеристическая функция действительная, то она обязательно четная.

Доказательство.

Пусть - (действительная)  (из свойства 5)  . Это используется для отсеивания функций, которые «хотят» быть характеристическими, но не могут.

б) По характеристическими функции однозначно восстанавливается закон распределения случайной величины Х .

Доказательство.

Если Х- СВНТ и E_x(t) удовлетворяем условиям Дирихле  плотность f_x(x) существует, причем: (3)

Пример 3. Пусть Х-СВНТ, причем задана характеристическая функция . Найти f_x(x).

Решение.

По формуле (3)  ==

=,

Х – распределен по Коши.

Пример 3. Пусть Х~N(m,). Вычислить E_x(t).

Решение.

По формуле (1):

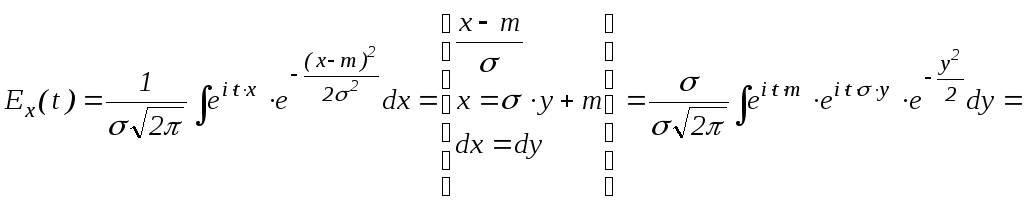= - характеристическая функция общего нормального распределения.