Лекции / Лекции (МП-3 Земсков) / Лекции (word) / Лекци10

Лекция 10

Необходимость. Пусть Х и Y - независимые, т.е. по определению Fx,y(x,y)=F_X(x)F_Y(y), для любых x,y,  R. Пусть (x_i,y_i)  E_X,Y - произвольный дискрет. Выберем столь малые x_i и y_i, чтобы прямоугольник П(x_i,y_i) с центром в этой точке и вершинами ((x_ix_i),(y_i y_i)) не содержал никаких других дискретов, кроме этого.

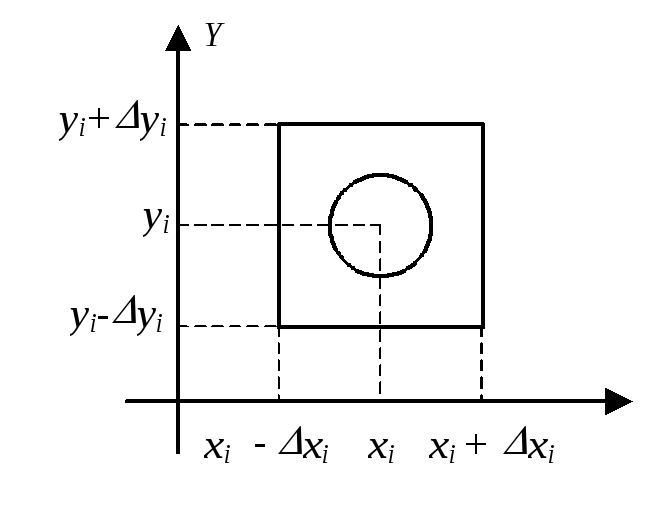
Pij=(по определению)=P{X=x_i, Y=y_i}=(по построению)=P{X,Y П(x_i,y_i)}=F_X,Y(x_i+x_i , y_i+ y_i)+ F_X,Y(x_i -x_i , y_i - y_i) - F_X,Y(x_i -x_i , y_i + y_i) -F_X,Y(x_i+x_i , y_i -y_i)== F_X(x_i+x_i) F_Y( y_i+ y_i)+ F_X(x_i -x_i) F_Y( y_i - y_i) - F_X(x_i - x_i) F_Y( y_i+ y_i) - F_X(x_i+x_i) F_Y( y_i - y_i)=

F_Y(y_i-y)(F_X(x_i+x)-F_X(x_i -x)) - F_Y(y_i - y)(F_X(x_i - x) -F_X(x_i -x))=

( F_X(x_i + x)- F_X(x_i - x))( F_Y( y_i+ y_i) - F_Y( y_i - y_i))

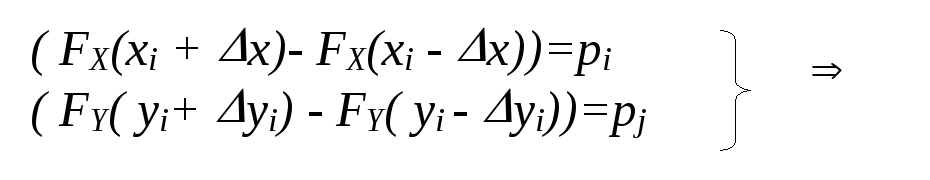
П(x_i,y_i)}= ( F_X(x_i + x)- F_X(x_i - x))( F_Y( y_i+ y_i) - F_Y( y_i - y_i))=p_ip_j

Теорема доказана.

Примечание. В теореме 9.1 устанавливается так называемое локальное условие независимости случайных величин X и Y. Согласно этому локальному определению независимости, распределение из примера 1 соответствует распределению независимых компонент X и Y.

Пример 1. Один раз подбрасываются игральные кости. Определить следующие эксперименты:

Х - индикатор числа очков, кратное 2 (индикатор четности)

Y - индикатор числа очков, кратное 3 (индикатор кратности 3)

1. описать закон распределения случайного вектора (X , Y);

2. определить, зависимые или нет компоненты X и Y;

3. вычислить функцию распределения вектора (X , Y);

Решение.

1) По определению индикатора: E_X={0,1}, E_Y={0,1}  E_X,Y  {(0,0); (0,1); (1,0); (1,1)}

Перейдем к множеству элементарных исходов .. Получаем таблицу:

	1	2	3	4	5	6
X	0	1	0	1	0	1
Y	0	0	1	0	0	1

Основная таблица (выгодно заполнять таблицу снаружи, поэтому заполним окаймление таблицы):

Достаточно вычислить одну клетку, тогда остальные заполняются по нормировке.

P_0,0=P{X=0, Y=0}=P(1)+P(5)=

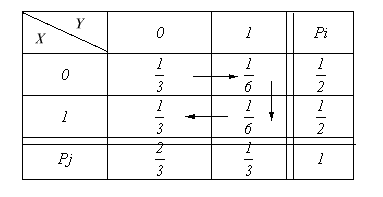
2) Проверим каждую клетку таблицы: если локальное условие выполняется везде, то X и Y независимы.

Pij=PiPj для всей таблицы  X и Y независимы (по теореме 9.1)

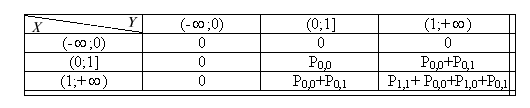
3) Построим функцию распределения.

?? ?

?

?

?

?

?

?

Будем захватывать точки прямым углом. F_X,Y=P{(x,y) Г(x,y)}=

(x_i,y_j) Г(x,y)

§3.3 Числовые характеристики случайного вектора.

1) Момент распределения.

_k,s=

_k,s=

k+s - суммарный порядок момента

	Начальные моменты	Центральные моменты
k+s=0	0,0	0,0=1
k+s=1	1,0== ==|Pij=Pi|= ==mx 0,1=mx	1,0=0
	0,1== =| рассуждаем аналогично|= my 0,1= my	0,1=0
k+s=2	2,0=M[X2]	2,0=Dx
	0,2=M[Y2]	0,2=Dy
	1,1=M[XY]	1,1=Cov(X,Y) - ковариация 1,1= Cov(X,Y)=KX,Y X,Y= - нормированная ковариация или коэффициент корреляции

Пример 2. Вычислить коэффициент корреляции для примера 1.

Решение. Из первой таблицы следует:

m_X=; m_Y=;

_1,1; _1,1= _1,1 - m_X m_Y

§3.4 Случайные векторы непрерывного типа (СВНТ) и их законы распределения.

Определение: Двумерный случайный вектор (X,Y) называется двумерным случайным вектором непрерывного типа, если множество типа континуум на плоскости и существует такая непрерывная и интегрируемая по Риману в бесконечных пределах функция f _X,Y(x,y), называемая плотностью распределения вероятности случайного вектора (X,Y) (или плотность совместного распределения компонент) такая, что имеет место равенство:

F_X,Y(x,y)= (1)

Следствия.

1) F_X,Y(x,y) - непрерывная на всей плоскости по двум переменным.

2) f_X,Y

3) (условие нормировки)

(F_X,Y(+,-)=1)

4)

Доказательство. Имеем: F_X,Y(x,+ )=Fx(x) по свойству функции распределения. по формуле (1) следует, что F_X(x)= . Но f_x(x)=(x)  (x)=

Свойство доказано.

5)Если (x,y) - точка непрерывности плотности, то f_X,Y=(из (1))

6) Понятие "элемента вероятности" :

f_X,Y(x,y)dxdy=P{(x,y) П(x,y)}

(вероятность попадания в прямоугольник П(x,y))

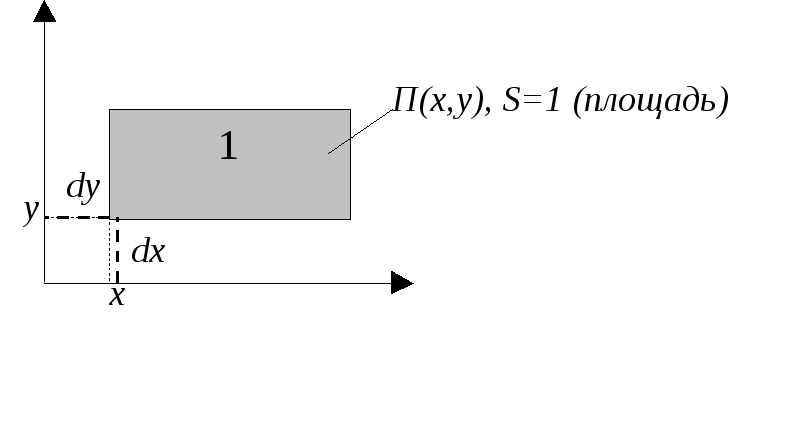
7) Пусть G-некоторая область на плоскости, тогда вероятность попадания в эту область:

P{(x,y) G}=

Нужно разбить всю плоскость на элементы dxdy и просуммировать.