Лекция 11.

Определения: случайные величины X и Y рассматриваются как компоненты некоторого вектора, называются независимыми, если функция распределения

F(x,y)=F_x(X)F_y(Y), (расщепляется на произвольные составляющие).

(x,y) R².

Следствие (локальное определение независимости).

Из (1)  (2)

(плотность также должна расшепляться).

Это определение обобщается на вектор  размерности ( количество случайных величин, рассматриваемых в одном и том же вероятностном пространстве).

Пример 1. Пусть плотность вектора имеет вид

(x,y) R².

Является X и Y независимыми?

Решение.

По свойству плотности

Полученная плотность является распределением Коши.

Аналогично, 

 независимы.

Пример 2. Пусть Х_1, Х₂,…Х_n – независимы и X_kN(m_k,_k).

Построить плотность совместного распределения компонент вектора Х=(х₁,х₂…х_n).

Решение.

В силу (2) для общего случая n-мерного вектора:

, 

-

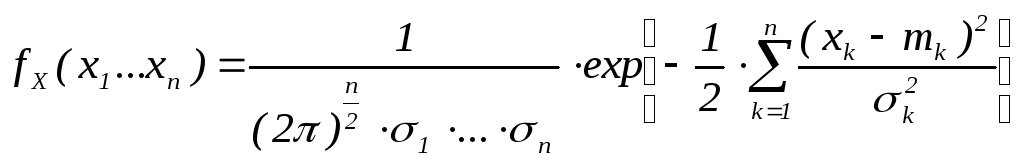плотность n-мерного распределения с независимыми компонентами.

Замечание. Если X и Y – нормальны, но зависимы, то плотность вектора (X,Y) записывается следующим образом:

где С – нормировочная константа;

Q – неотрицательная определенная квадратичная форма двух переменных.

Глава 4. Функция от случайных величин.

§ 4.1. Теоремы о математическом ожидании функций.

Определение. Пусть на вероятностном пространстве {Ω,F,P} заданы случайные величины X(w) и Y(w) и z=(x,y) – действительная функция от двух переменных  Z=(X,Y), при определенных условиях на случайные величины X и Y будет являться случайной величиной определенной на том же вероятностном пространстве.

? Как вычислить математическое ожидание M[Z]?

Теорема 11.1. (новая формула для математического ожидания).

Пусть X – случная величина дискретного типа с заданным законом распределения. Пусть математическое ожидание M[X] существует. 

(3)

Доказательство.

Нам известна следующая формула из определения математического ожидания:

. (4)

Отличие формул (3) и (4): в (3) возможны повторения значения X(w_i).

Разобьем все значения X(w_i) на блоки:

B_k={w_iX(w_i)=x_k, iI_k},

где I_k – множество индексов k-го блока.

По правилам теории вероятностей мы можем записать:

Преобразуем (4) следующим образом:

что и требовалось доказать.

Теорема 11.2. (о математическом ожидании функции).

Пусть Х – СВДТ с заданным законом распределения и Z=(X) – новая случайная величина, где (х) – некоторая действительная функция действительной переменной.

Тогда (5)

Доказательство.

Используем разбиение на блоки из Т.11.1. 

что и требовалось доказать.

Обобщение теоремы 11.2.

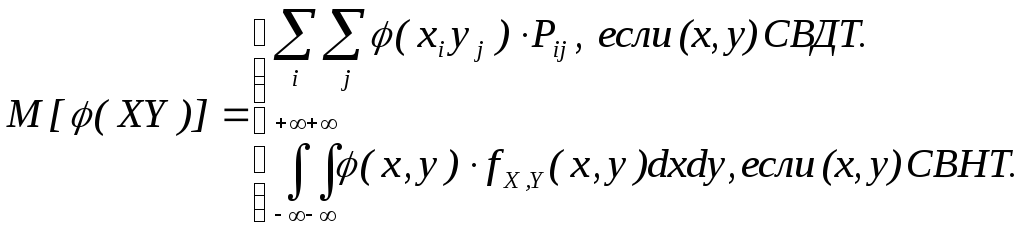(6)

Замечание. Как показывает (6) для вычисления математического ожидания от функции Z=(X,Y) не надо знать закон распределения этой новой случайной величины, а достаточно знать закон распределения, того вектора, от которого она зависит.

Пример 3. На круговом индикаторе цели радиуса а наблюдается световое пятно, отраженное импульсом от цели. Будем считать, что на этапе поиска цели пятно появляется наудачу в  месте экрана.

Найти среднее (по распределению) значение расстояния от центра экрана до светового пятна.

Решение.

Формализуем задачу: пусть (X,Y) – случайные координаты центра пятна (точка). По описанию эксперимента:

(X,Y) R (в круге радиуса a) 

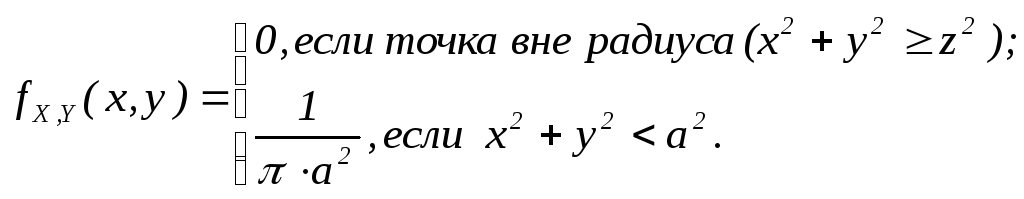
Нас интересует M[Z],

где

По формуле (6):

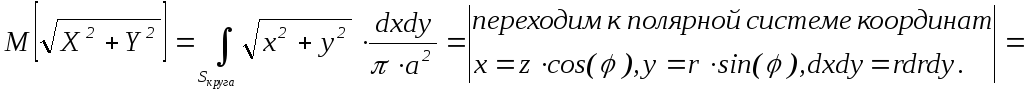
Замечание. Формула (6) позволяет оправдать следующие обозначение для моментов случайного вектора ( типа):

что совпадает с определением из лекции10.

В частности, , то есть дисперсия – математическое ожидание квадрата случайной величины.

K_x,y=, где

K_x,y – ковариация.

§ 4.2. Свойства числовых характеристик случайного вектора.

1. Линейность.

Доказательство.

Для дискретного случая:

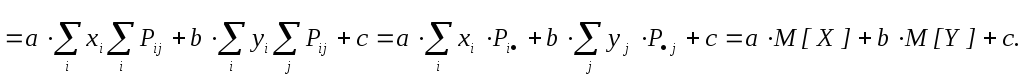
Следствия из свойства 1.

1. M[c]=c;

2. M[aX]=aM[X] (математическое ожидание как спектр);

3. Если X ≥ 0  M[X]≥ 0  Y ≥ X  M[Y] ≥ M[X].

2. 

Доказательство.

По новому определению дисперсии:



Достаточно возвести в квадрат и воспользоваться свойством 1.

Лекция 12.

Следствия из свойства 2.

1)

2) D[X] ≥ 0;

3) D[c]=0;

4) Если D[X]=0  X-const.

Свойство 2 в общей формулировке:

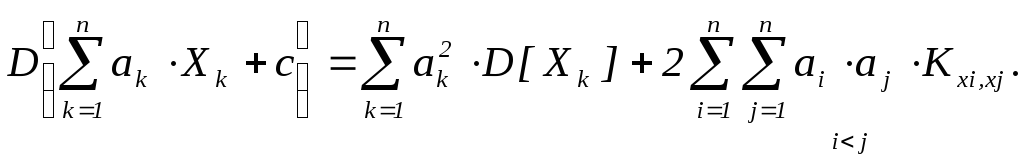
Определение. Случайные величины X и Y называются некоррелированными, если K_X,Y=0.

3. M[XY]=M[X]M[Y]+K_X,Y.

Доказательство.

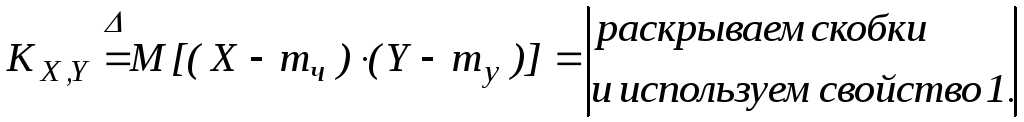
На практике это свойство используется для следующей записи:

Следствия из свойства 3.

Если K_X,Y =0, то M[XY]=M[X]M[Y]

Замечание. Для большого числа случайных величин (≤ 3) некоррелированности недостаточно для распределения математического ожидания  должны быть независимы в совокупности.

M[XYZ]=M[X]M[Y]M[Z], если X,M, Y, Z независимы в совокупности.

4. Если X и Y независимы  D[XY]=D[X]D[Y]+m²_x D[Y]+ m²_y D[X]

5. Неравенство Коши-Буняковского

M ²[XY]=M[X ²]M[Y ²]

Доказательство.

Рассмотрим неравенство M[(aX+Y)²] ≥ 0,  а  R или M[a ²X+2aXY+Y] (по свойству линейностью) = a ²M[X ²]+2aM[XY]+M[Y ²] ≥ 0  (дискриминант =

= 4 M ²[XY]-4 M[X ²]M[Y ²] ≤ 0  результат.

Следствия из свойства 5.

1) При Y0  M ²[X] ≤ M[X ²] (или m²_x ≤ ₂ ) или: если  ₂   ₂ m_x=₁

Доказать, что если  ₄, то автоматически существует ₁, ₂, ₃, используя неравенство Коши-Буняковского.

2) К_Х,Y ≤ _X_Y

Доказательство. В неравенстве Коши-Буняковского заменим X, Y   К_Х,Y ≤ _X_Y

Определение Число называется коэффициентом корреляции случайных величин X и Y .

Определение. Пусть X случайная величина с характеристиками m_x и _x 

Преобразованная величина ,

называется стандартизированной случайной величиной, так как

M[U]=0, D[U]=1.

5. Преобразуем случайные векторы (X,Y) в (U,V), где

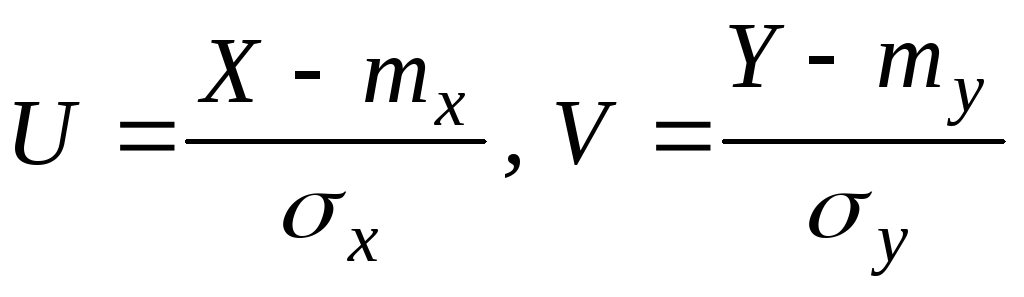
(вектор (X,Y) подвергли преобразованию стандартизации), тогда _U,V=_X,Y.

Доказательство.

Таким образом, показано, что операция стандартизации не меняет коэффициента корреляции.

5. 

Доказательство.

Следует из определения _X,Y и следствия 2 из свойства 5.

5. Пусть Y=aX+b 

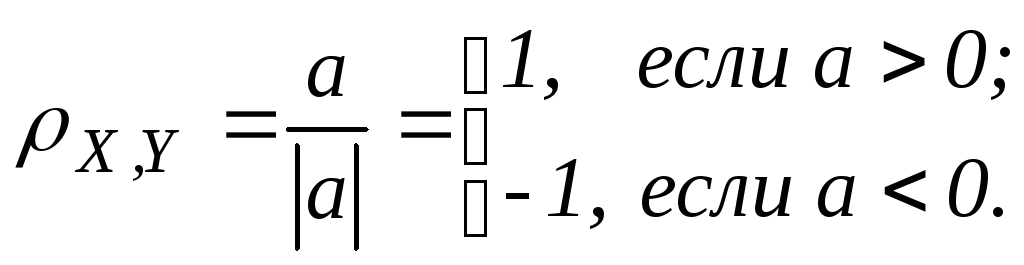
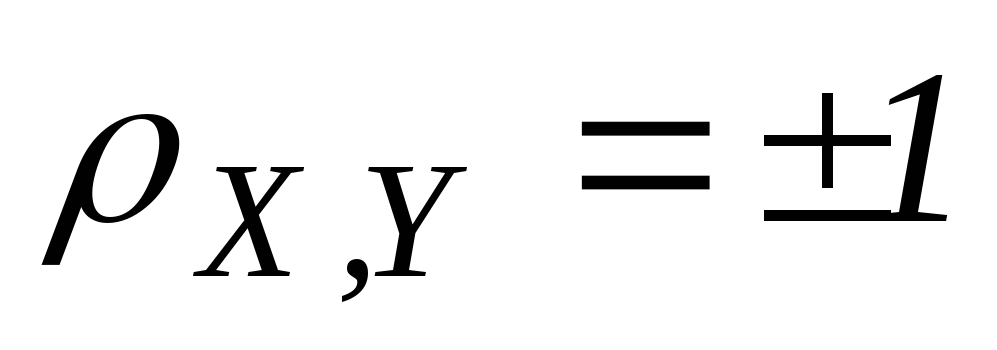
Обратно: Если  Y=aX+b,

где a>0, если

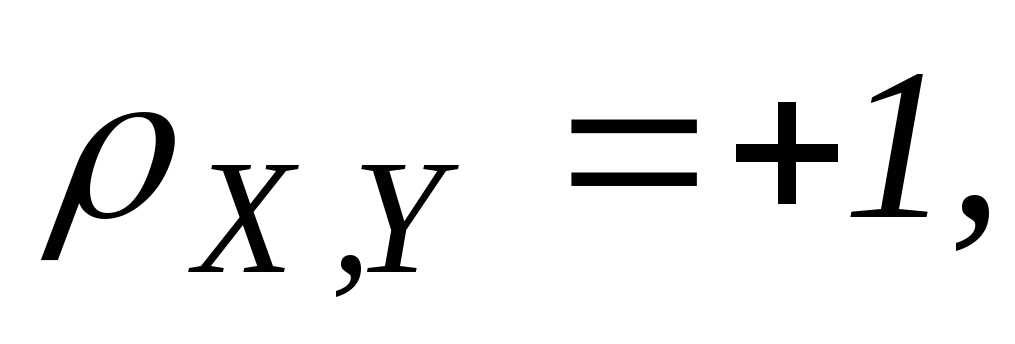
a<0, если

Доказательство.

Пусть Y=aX+b  M[Y]=aM[X]+b,

D[Y]=D[aX+b]=a²D[X].

Обратно.

Пусть 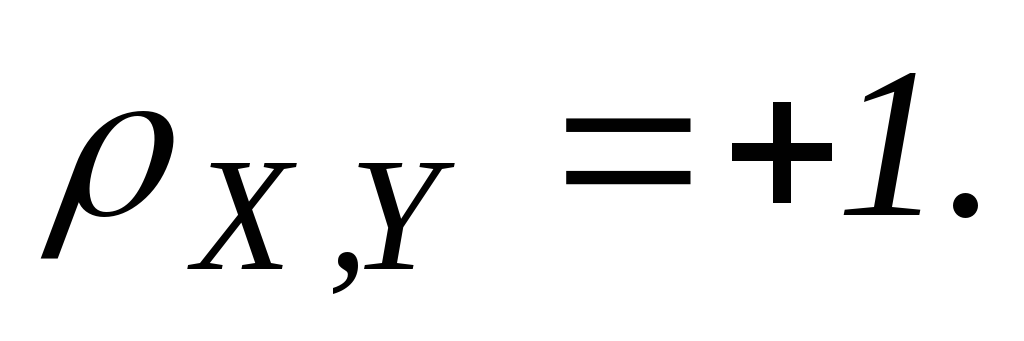Перейдем от (X,Y) к (U,V) путем преобразования стандартизации  рассмотрим

.

Так как D[U-V]=0, то U-V=const=c.



;



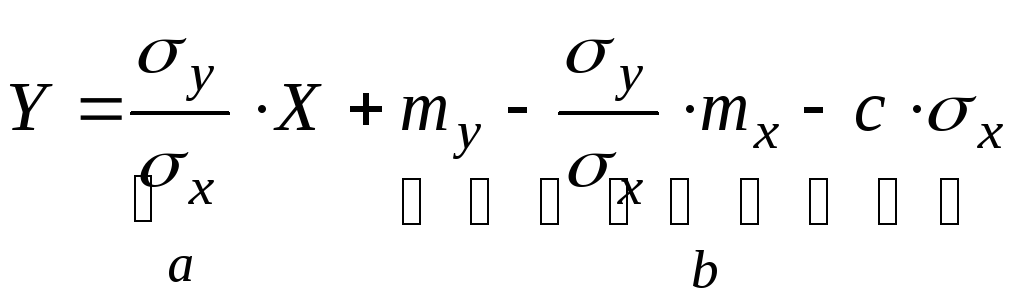
Y=aX+b, где a>0.

Случай 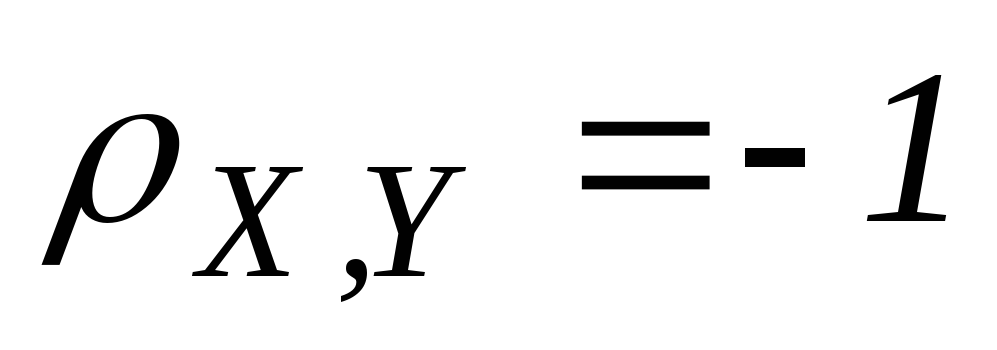рассматривается аналогично.

5. Из независимости X и Y  некоррелированность X и Y. Обратное не верно.

Доказательство.

Пусть X и Y СВНТ и независимы 



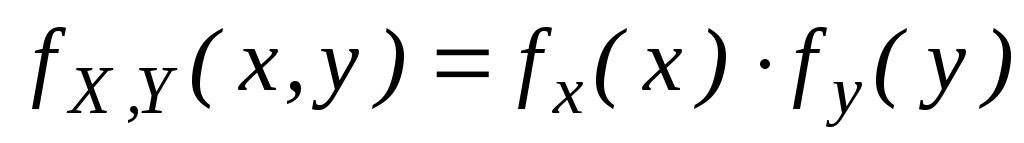
Тот факт, что обратное неверное демонстрирует следующий пример.

Пример 1. Пусть (X,Y) – C вектор дискретного типа с законом распределения, описываемым следующей таблицей.

X\Y	-1	0	1
-1	1/8	0	1/8
0	0	1/2	0
1	1/8	0	1/8

1. Показать, что 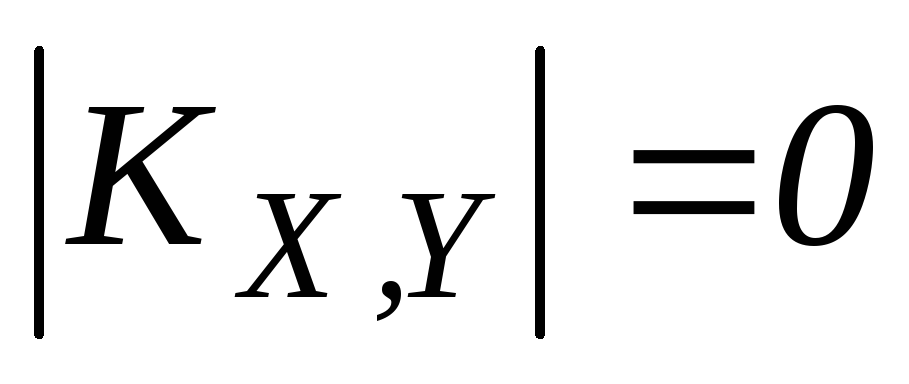(используя

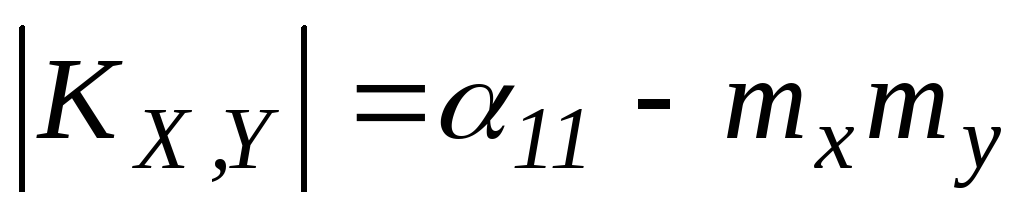
2. Заметим, что 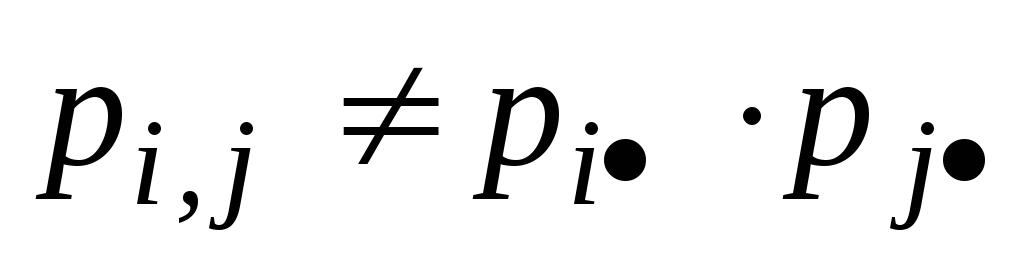ни в одной кдетке.

Пример 2. Пусть (X,Y) ~R (круге радиуса а). Показать, что , но X и Y – зависимы.

§ 4.3. Характеристическая функция и ее свойства.

Определение. Комплекснозначная функция действительного переменного t, определяемая равенством

, называется характеристической функцией случайной величины Х.

Воспользуемся формулой Эйлера:

Договоримся, что свойства линейности математического ожидания распространяется и на комплексные случайные величины.

Теорема 12.1.

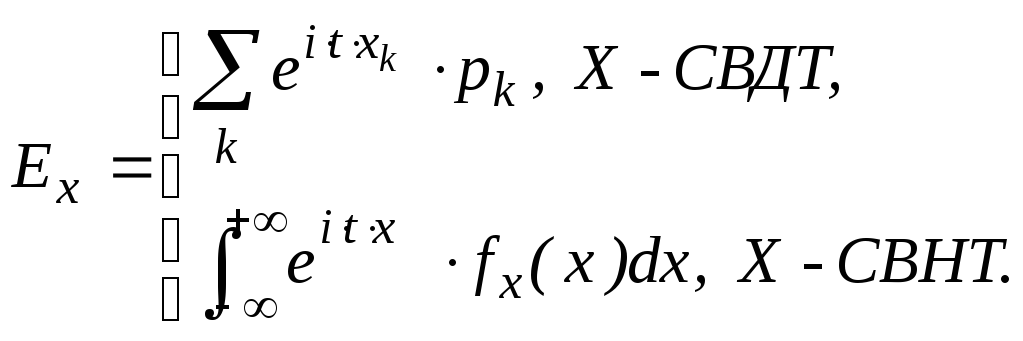
Доказательство.

Для определения линейности, пусть Х-СВНТ  =

=(по теореме 11.2) = (по формуле Эйлера)=

=, что и требовалась доказать.