
4241, 4242(ТАУ-без MATLAB) / КР / ТАУ. МетодУказКВыпКурсРаб.МалПоля
.pdfрий максимальной точности) и критерий минимума расхода энергии. При синтезе систем управления методом АКОР используются ма-
тематические модели систем в форме пространства состояний.
В данном конкретном случае общая математическая модель объекта управления (ДПТ) в форме пространства состояний имеет полу-
/ |
h |
|
612963 |
67402 |
0 |
h |
||
ченный ранее вид (3.11): |
4.916 |
|
0 |
|
0l · kh l 2 |
|||
c/1 kh l k |
|
|
||||||
|
hQ |
|
0 |
0 |
1 |
|
0 |
hQ |
|
|
12963 |
|
|
· mi n |
|
||
|
|
2 k |
0 |
60.115l |
. |
|||
b |
|
0 |
0 |
|
|
i |
; |
|
0 1 0 |
h |
|
|
0 0 |
i |
|||
|
|
|
|
h |
|
2 m0 0n · mi n |
||
m n m0 0 1n · khQl |
||||||||
` |
|
|
|
|
|
|
|
|
Здесь
– ток якоря;
– частота вращения вала якоря;
Q– угол поворота вала якоря;
– напряжение питания ДПТ;
|
н – момент нагрузки ДПТ; |
– частота вращения вала якоря;
– угол поворота вала якоря.
Синтез приводов методом АКОР удобно проводить при условии, |
|||||||||
что на систему не действует возмущающее воздействие |
i н. В |
||||||||
этом случае модель (3.11) примет следующий вид: |
h |
|
|||||||
|
/ |
h |
612963 |
67402 |
0 |
|
|
||
|
c/1 kh l k |
4.916 |
|
0 |
0l |
· kh l 2 |
|
||
|
|
hQ |
0 12963 1 |
0 |
|
hQ |
|
||
(3.16) |
|
|
2 k |
0 |
l · i |
|
|
; |
|
b |
|
|
|
. |
|
||||
|
|
0 1 |
0 |
h |
0 |
|
|
||
|
|
0 |
|
|
|
||||
|
` |
m n m0 0 |
|
h |
|
|
|
||
|
1n · khQl |
2 m0n · i |
|
||||||
Далее на основании модели (3.16) следует записать модели ДПТ в
-81-
форме пространства состояний отдельно для случаев, когда выходной
переменной является частота вращения вала якоря |
и когда |
якоря |
. |
выходной переменной является угол поворота вала y A |
|
y
В первом случае (он удобен при синтезе частотного привода), когда выходным сигналом системы является частота вращения вала яко-
|
c/1/ |
mh n |
m612963 |
|
67402n · mh n 2 |
|||||||
ря A, получается модель: |
|
|
|
|
|
h |
|
|||||
|
|
h |
|
|
4.916 |
|
0 |
|
|
|||
(3.17) |
|
|
|
|
12963 |
n · i |
|
. |
||||
|
b |
|
|
< |
2 m |
= |
0 |
|
|
; |
||
|
|
|
0 1 |
|
h |
<0= |
|
|
||||
|
|
|
|
|
· mh n 2 |
· i |
|
|||||
`
Во втором случае (он удобен при синтезе позиционного привода), когда выходным сигналом системы является угол поворота вала якоря
|
µ |
x |
612963 |
67402 |
0 |
x |
|
, получается модель: |
|
0 |
0l |
· kx l 2 |
|||
|
cµ¶ kx l |
k 4.916 |
|||||
|
|
xQ |
0 |
12963 1 |
0 |
xQ |
|
(3.18) |
|
|
2 k |
0 |
l · u |
|
; |
b |
|
|
. |
||||
|
|
<0 0 |
0 |
h |
|
||
|
|
1= |
· khQl 2 |
<0= · i |
|||
|
|
|
|
|
h |
|
|
|
оптимальных регуляторов для частотного и позиционного |
||||||
Расчет |
` |
|
|
|
|
|
|
приводов методом АКОР сводится к решению матричных уравнений Риккати с известными начальными условиями.
Матричным алгебраическим уравнением Риккати называют не-
линейное матричное уравнение следующего вида: |
|
|
(3.19) |
‹o 2 o¯‹ 6 ‹rr¯ 2 Œ 0 |
|
Чаще всего полагают, что матрица Œ является. |
единичной. |
|
Процедура АКОР состоит в отыскании матрицы коэффициентовs усиления регулятора. Матрица коэффициентов усиления регулятора
определяется по следующей формуле (уравнение Лаурье): s 6‹:r.
-82-
Здесь ‹: – положительно-определенное решение (матрица) урав-
нения (3.19).
Таким образом, процедура АКОР состоит из трех операции:
1. Решение каким-либо методом системы нелинейных алгебраи-
ческих уравнении (матричного уравнения Риккати). |
|||||
‹ |
: |
… 0 |
. |
|
|
2. Выделение из всего множества найденных решений матрицы |
|||||
3. Вычисление искомой матрицы коэффициентов усиления регу- |
|||||
лятора |
|
по формуле (12.4). |
|||
|
|
|
работе для решения матричных алгебраических уравне- |
||
В данной |
|
s |
|
||
ний Риккати используется среда MATLAB. Ниже перечислены необ- |
|||||
ходимые для этого функции среды MATLAB: |
|||||
eye() |
|
|
|
– |
создание единичных матриц; |
transp() |
|
|
– |
транспонирование матриц; |
|
ss() |
|
|
|
– создание модели в пространстве состояний; |
|
care() |
|
|
|
– отыскание решений непрерывных алгебраических |
|
|
|
|
|
|
уравнений Риккати; |
augstate() |
|
– увеличение количества выходных переменных мо- |
|||
|
|
|
|
|
дели за счет присоединения переменных состояния |
квектору выходных переменных модели.
3.14.1.Синтез оптимального частотного привода
Ниже показан процесс создания в среде MATLAB ss-модели ДПТ по системе уравнений (3.17):
»A1 = [-12963, -7402; 4.916, 0];
»B1 = [12963; 0];
»C1 = [0, 1];
»D1 = [0];
»S1 = ss(A1, B1, C1, D1);
Переходная характеристика ДПТ по управляющему воздействию для данной модели имеет вид, показанный на Рис. 3.47. Как видно, она совпадает с переходной характеристикой ДПТ, построенной по соответствующей передаточной функции (см. Рис. 3.6) и с соответствующей переходной характеристикой, полученной в результате симуляции ДПТ (см. Рис. 3.20).
-83-
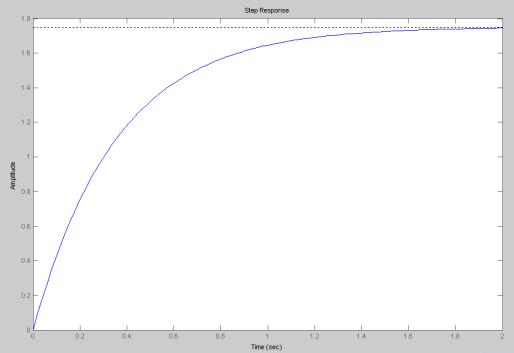
Рис. 3.47. ПХ ДПТ по управляющему воздействию, построенная для модели (3.17).
Далее приводится последовательность действий по синтезу частотного привода методом АКОР. 2 ¹ 2
1. Создание единичной матрицы размеров :
»Q1 = eye(2, 2);
2.Получение решения уравнения Риккати:
»P1 = care(A1, B1, Q1)
P1 =
0.0000 0.0000
0.0000 0.2152
3.Определение матрицы коэффициентов усиления регулятора:
»C1 = - P1 * B1
C1 =
-0.4144 -0.5805
-84-
4.Создание модели регулятора в форме пространства состояний:
»R1 = ss(transp(C1))
d =
u1 u2
y1 -0.41437 -0.58053
Static gain.
5.Увеличение количества выходных переменных модели объекта управления за счет присоединения переменных состояния к вектору выходных переменных модели:
»S1 = augstate(S1)
a = |
|
|
|
x1 |
x2 |
x1 |
-12963 |
-7402 |
x2 |
4.916 |
0 |
b = |
|
|
|
u1 |
|
x1 |
12963 |
|
x2 |
0 |
|
c = |
|
|
|
x1 |
x2 |
y1 |
0 |
1 |
y2 |
1 |
0 |
y3 |
0 |
1 |
d = |
|
|
|
u1 |
|
y1 |
0 |
|
y2 |
0 |
|
y3 |
0 |
|
Continuous-time system.
6.Получение модели синтезированного оптимального частотного привода в форме пространства состояний. Для этого удобно применять функцию:
feedback(sysl, sys2, feedin, feedout)
Данная функция позволяет реализовать более общую форму
-85-
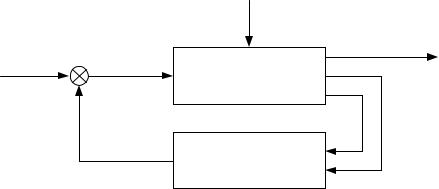
встречно-параллельного соединения двух подсистем sysl и sys2. В случае оптимального частотного привода данное соединение должно выглядеть так, как показано на Рис. 3.48.
|
M Н (t) |
ω(t) |
|
ωз (t) |
δ (t) |
||
|
|||
|
I (t) |
ω(t) |
|
|
|
Рис. 3.48. Структурная схема оптимального частотного привода.
У функции feedback() вектор feedin содержит индексы входного вектора объекта регулирования и определяет, какие его переменные будут использоваться при организации контура обратной связи. Вектор feedout определяет, какие выходы объекта регулирования используются для организации контура обратной связи. Результирующая ss-модель привода имеет те же входные и выходные векторы (с сохранением их размеров), что и объект регулирования после увеличения с помощью п. 5 количества его выходных переменных.
По умолчанию функция предполагает, что контур замыкается отрицательной обратной связью. Для обеспечения положительной обратной связи следует при вызове функции в конце добавить пятый аргумент, равный единице.
В результате в данном конкретном случае получается следующая ss-модель оптимального частотного привода:
» M1 = feedback(S1, R1, [1], [2, 3], 1)
a = |
|
|
|
x1 |
x2 |
x1 |
-18334 |
-14927 |
x2 |
4.916 |
0 |
b = |
|
|
|
u1 |
|
x1 |
12963 |
|
x2 |
0 |
|
-86-

c = |
|
|
|
x1 |
x2 |
y1 |
0 |
1 |
y2 |
1 |
0 |
y3 |
0 |
1 |
d = |
|
|
|
u1 |
|
y1 |
0 |
|
y2 |
0 |
|
y3 |
0 |
|
Continuous-time system.
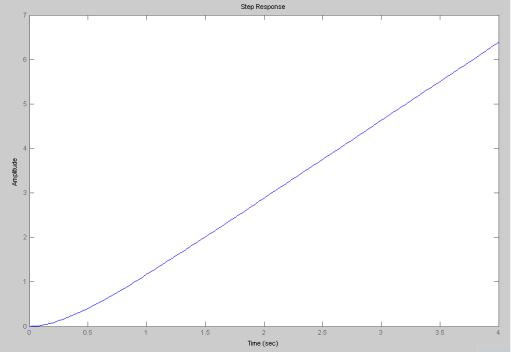
На Рис. 3.49 изображен построенный при помощи полученной ssмодели график переходной характеристики синтезированного оптимального частотного привода по задающему воздействию, в котором в качестве выходного сигнала используется частота вращения якоря.
Рис. 3.49. ПХ оптимального частотного привода по задающему воздействию с частотой вращения вала на выходе.
3.14.2. Синтез оптимального позиционного привода
Ниже показан процесс создания в среде MATLAB ss-модели ДПТ по системе уравнений (3.18):
-87-
»A2 = [-12963, -7402, 0; 4.916, 0, 0; 0, 1, 0];
»B2 = [12963; 0; 0];
»C2 = [0, 0, 1];
»D2 = [0];
»S2 = ss(A2, B2, C2, D2);
Переходная характеристика ДПТ по управляющему воздействию для данной модели имеет вид, показанный на Рис. 3.50. Как видно, она совпадает с переходной характеристикой ДПТ, построенной по соответствующей передаточной функции (см. Рис. 3.8) и с соответствующей переходной характеристикой, полученной в результате симуляции ДПТ (см. Рис. 3.24).
Рис. 3.50. ПХ ДПТ по управляющему воздействию, построенная для модели (3.18).
Далее приводится последовательность действий по синтезу позиционного привода методом АКОР. 3 ¹ 3
1. Создание единичной матрицы размеров :
»Q2 = eye(3, 3);
2.Получение решения уравнения Риккати:
»P2 = care(A2, B2, Q2)
-88-
P2 =
0.0000 0.0001 0.0001
0.0001 0.2806 0.2877
0.0001 0.2877 1.3789
3.Определение матрицы коэффициентов усиления регулятора:
»C2 = - P2 * B2
C2 =
-0.4144 -0.8079 -1.0000
4.Создание модели регулятора в форме пространства состояний:
»R2 = ss(transp(C2))
d = |
|
|
|
|
u1 |
u2 |
u3 |
y1 |
-0.41443 |
-0.80794 |
-1 |
Static gain.
5.Увеличение количества выходных переменных модели объекта управления за счет присоединения переменных состояния к вектору выходных переменных модели:
»S2 = augstate(S2)
a = |
|
|
|
|
x1 |
x2 |
x3 |
x1 |
-12963 |
-7402 |
0 |
x2 |
4.916 |
0 |
0 |
x3 |
0 |
1 |
0 |
b = |
|
|
|
|
u1 |
|
|
x1 |
12963 |
|
|
x2 |
0 |
|
|
x3 |
0 |
|
|
c = |
|
|
|
|
x1 |
x2 |
x3 |
y1 |
0 |
0 |
1 |
-89-
y2 |
1 |
0 |
0 |
y3 |
0 |
1 |
0 |
y4 |
0 |
0 |
1 |
d = |
|
|
|
|
u1 |
|
|
y1 |
0 |
|
|
y2 |
0 |
|
|
y3 |
0 |
|
|
y4 |
0 |
|
|
Continuous-time system.
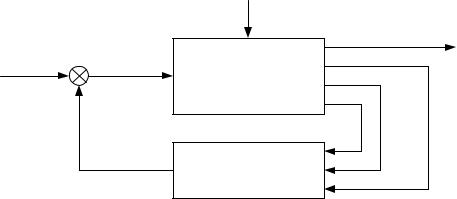
6.Получение модели синтезированного оптимального позиционного привода в форме пространства состояний. Для этого также удобно применять функцию feedback(). В случае оптимального позиционного привода реализуемое данной функцией соединение должно выглядеть так, как показано на
Рис. 3.51.
|
M Н |
(t) |
|
ϕ(t) |
|
|
|
|
|
ϕз (t) |
δ (t) |
|
|
|
|
|
|
I (t) |
ω(t) |
|
|
|
|
|
|
|
|
|
ϕ(t) |
Рис. 3.51. Структурная схема оптимального позиционного привода.
В результате в данном конкретном случае получается следующая ss-модель оптимального позиционного привода:
» M2 = feedback(S2, R2, [1], [2, 3, 4], 1)
a = |
|
|
|
|
x1 |
x2 |
x3 |
x1 |
-18335 |
-17875 |
-12963 |
x2 |
4.916 |
0 |
0 |
x3 |
0 |
1 |
0 |
b =
u1
-90-
