
4241, 4242(ТАУ-без MATLAB) / КР / ТАУ. МетодУказКВыпКурсРаб.МалПоля
.pdf
|
/ |
h |
|
612963 |
67402 |
0 |
|
· |
||||
|
c/1 kh l k |
4,916 |
|
0 |
|
0l |
||||||
|
|
hQ |
|
0 |
|
|
0 |
1 |
|
0 |
|
|
|
|
|
12963 |
|
|
|
· mi n |
|||||
(3.13) |
b |
|
2 k |
0 |
|
|
60,115l |
|||||
|
|
|
0 |
|
|
h 0 |
|
|
i |
|
||
|
|
< |
|
= |
|
h |
|
< |
|
= |
|
|
|
` |
|
· khQl 2 |
|
· |
|||||||
|
0 0 1 |
|
0 0 |
|
||||||||
h kh l 2 hQ
;.
mii n
3.5. ОПРЕДЕЛЕНИЕ УСТОЙЧИВОСТИ ОБЪЕКТА ПО КОРНЯМ ХАРАКТЕРИСТИЧЕСКОГО УРАВНЕНИЯ
Одной из важнейших характеристик системы автоматического управления является ее устойчивость. Причем если, к примеру, показатели точности определяют степень полезности и эффективности системы, то от устойчивости зависит принципиальная работоспособность системы, т. к. система управления, не обладающая устойчивостью, вообще не способна выполнять функции управления. Неустойчивая система автоматического управления может привести объект, да и саму себя, в аварийное состояние.
Устойчивость – это свойство системы возвращаться в исходное состояние равновесия после прекращения воздействия, выведшего ее из этого состояния. Неустойчивая система не возвращается в исходное состояние, а непрерывно удаляется от него.
Общая формулировка устойчивости системы: для устойчивости линейной системы управления необходимо и достаточно, чтобы действительные части всех корней характеристического уравнения системы были отрицательными. Если хотя бы один корень характеристического уравнения имеет положительную действительную часть, то система будет неустойчивой.
Устойчивость системы зависит только от корней характеристического уравнения и не зависит от характера внешних воздействий, оказываемых на систему. Устойчивость – это внутреннее свойство системы, присущее ей вне зависимости от внешних условий.
Используя геометрическое представление корней на комплексной плоскости в виде векторов или точек, можно дать вторую формулировку общего условия устойчивости: для устойчивости линейной системы необходимо и достаточно, чтобы все корни характеристического уравнения находились в левой полуплоскости. Если хотя бы один корень характеристического уравнения находится в правой полуплоско-
-31-
сти, система будет неустойчивой.
Для определения устойчивости исследуемого объекта или системы управления удобно воспользоваться средой компьютерного моделированияo MATLAB. Если известна матрица состояний объекта (системы) , то тогда характеристическое уравнение объекта (системы) может быть представлено в виде:
det(λE − A) = 0 .
Решая это уравнение в среде MATLAB можно найти корни характеристического уравнения системы управления и тем самым оценить устойчивость системы. Однако, как известно, корни характеристического уравнения системы управленияo совпадают с собственными числами ее матрицы состояний .
Вычисление собственных значений и собственных векторов мат-
ращение к ней с передачей в нее матрицыo o позволяет получить вектор собственных значений матрицы , т. е. набор корней характеристического уравнения системы.
рицы в среде MATLAB осуществляет функция eig(). Обычное об-
При вычислении в среде MATLAB собственных значений матрицы состояний модели (3.12) получается следующий результат:
»A = [-12963, -7402; 4.916, 0];
»eig(A)
ans =
1.0e+004 *
-1.2960 -0.0003
Так как все корни характеристического полинома располагаются в левой полуплоскости комплексной плоскости корней, то исследуемый объект, описываемый моделью (3.12), является устойчивым.
При вычислении в среде MATLAB собственных значений матрицы состояний модели (3.13) получается следующий результат:
»A = [-12963, -7402, 0; 4.916, 0, 0; 0, 1, 0];
»eig(A)
ans =
1.0e+004 *
-32-

0 -0.0003 -1.2960
Так как первый корень характеристического полинома находится в центре координат, а остальные корни располагаются в левой полуплоскости комплексной плоскости корней, исследуемый объект, описываемый моделью (3.13), лежит на границе апериодической устойчивости.
3.6. ПОЛУЧЕНИЕ ПЕРЕДАТОЧНЫХ ФУНКЦИЙ ОБЪЕКТА
Имея математическую модель в виде системы уравнений (3.11), можно получить передаточную функцию исследуемой системы с по-
мощью следующей формулы: |
|
(3.14) |
w<x= s · <x · 3 6 o=V · r 2 v. |
Применяя формулу (3.14) вычислить соответствующие передаточные функции исследуемой системы удобно, например, в среде компьютерного моделирования MathCad (см. Рис. 3.2).
Рис. 3.2. Получение передаточных функций в среде MathCad.
Указывая вход и выход системы регулирования, можно записать передаточные функции отдельно (см. Табл. 3.5).
-33-
Табл. 3.5. Передаточные функции ДПТ.
№ |
Вход |
Выход |
Передаточная функция |
|
|
||||
1 |
Напря- |
Час- |
|
|
|
3.241 |
|
|
|
жение |
тота |
|
|
|
|
|
|||
|
|
|
wy7 5,085 · 10VRx 2 6,592x 2 1,851 |
||||||
|
Момент |
|
65,848 · 10 |
V{ |
x 6 7,581 · 10 |
V |
|
||
2 |
сопро- |
Час- |
|
||||||
|
тивле- |
тота |
|
|
|
||||
|
ния |
|
wмн7 5,085 · 10VRx |
2 6,592x 2 1,851 |
|||||
|
Напря- |
Угол |
|
3,241 |
|
|
|||
3 |
пово- |
|
|
|
|||||
жение |
|
|
|
||||||
|
|
рота |
wy] x · <5,085 · 10VRx |
2 6,592x 2 1,851= |
|||||
|
Момент |
Угол |
65,848 · 10 |
V{ |
x 6 7,581 · 10 |
V |
|||
|
сопро- |
||||||||
4 |
пово- |
||||||||
|
тивле- |
|
|
|
|||||
|
ния |
рота |
wмн] x · <5,085 · 10VRx 2 6,592x 2 1,851= |
||||||
3.7. ОПРЕДЕЛЕНИЕ УСТОЙЧИВОСТИ ОБЪЕКТА ПРИ ПОМОЩИ КРИТЕРИЕВ УСТОЙЧИВОСТИ
Устойчивость систем управления можно определять без отыскания корней характеристического уравнения. Для этого применяют различные критерии устойчивости.
Критерий устойчивости – это математическая формулировка некоторых условий относительно коэффициентов характеристического уравнения системы, при удовлетворении которых система управления будет являться устойчивой.
Критерии устойчивости по содержанию эквивалентны сформулированному ранее условию устойчивости.
Критерии устойчивости бывают алгебраические и частотные. Алгебраические критерии устанавливают необходимые и доста-
точные условия отрицательности корней в форме ограничений, накладываемых на определенные комбинации коэффициентов характеристического уравнения. В работе требуется для определения устойчивости применить алгебраический критерий Гурвица.
Частотные критерии определяют связь между устойчивостью системы и формой частотных характеристик системы. В работе требу-
-34-
ется для определения устойчивости применить частотный критерий Михайлова.
Критерий Гурвица удобен для исследования устойчивости систем до пятого порядка включительно. Дополнительно он позволяет получать аналитическое выражение (выражения) для границ области возможных значений какого-либо параметра (параметров) системы, в которой эта система остается устойчивой.
Критерий устойчивости Михайлова помимо определения самой устойчивости позволяет достаточно легко устанавливать, в каких пределах может изменяться тот или иной параметр системы управления без потери самой устойчивости.
3.7.1. Алгебраический критерий устойчивости Гурвица
Критерий Гурвица был сформулирован и доказан в 1895 г. немецким математиком А. Гурвицем (A. Hurwitz). Он разработал свой критерий, решая чисто математическую задачу – задачу исследования устойчивости решений линейного дифференциального уравнения.
Применительно к задачам теории управления критерий Гурвица
можно сформулировать следующим образом: линейная динамическая система управления, описываемая характеристическим уравнением
(3.15) |
: } |
|
|
}V |
|
|
|
}V |
|
|
} , |
|
и все |
|
|
|
положительны все |
|
|
|
коэффициентов |
|
|
||||||||
устойчива, если| x |
2 | x |
|
2 ~ 2 | |
0 |
x 2 | |
0 |
|0 |
|
, |
||||||
|
|
| |
|Q |
|R |
|
… |
|
|
|
|
|
||||
определителей Гурвица ∆0 |
следующего вида: |
|
|
|
|||||||||||
|
|
|
|
, 2 1 |
|
|
|
|
|
||||||
|
∆0 |
|: |
| |
|W |
|
… |
0 |
|
; 1, , |
. |
|
|
|
||
|
0 |
| |
Q |
|
… |
0 |
|
|
|
|
|
||||
|
|
… |
| |
|
|
|
|
|
|
|
|
||||
|
|
• … |
… |
… |
… .• |
|
|
|
|
|
|
||||
|
|
0 |
… |
… |
… |
|0 |
|
|
|
|
|
|
|
||
Если хотя бы один из определителей Гурвица отрицателен, то система управления является неустойчивой.
Матрицу, по которой вычисляют определители Гурвица, составляют следующим образом:
1.На главной диагонали записывают| |все коэффициенты характеристического уравнения от до } (в порядке возрастания индекса).
2.В каждом столбце выше диагональных коэффициентов записывают коэффициенты с последовательно возрастающими индексами, а ниже – с последовательно убывающими индексами.
-35-
3. На место коэффициентов с индексами больше |
, |
или меньше |
||||
нуля проставляют нули. |
|
|
|
|||
Пусть выполняется условие |
|
, причем все остальные опре- |
||||
|
|
|
Тогда, очевидно, система находится |
|||
делители Гурвица положительны.∆} 0 |
|
|
|
|||
на границе устойчивости. Так как |
} }V , |
|
|
|||
то условие ∆} 0 |
|
} |
|
|
||
распадается на одно из двух условий: |
|
|
||||
|
∆ | |
· ∆ |
|
|
|
|
Условию |} 0 |
|} 0 либо ∆}V 0. |
|
|
|||
соответствует один нулевой корень характери- |
||||||
стического уравнения, то∆есть наблюдается0 апериодическая граница устойчивости, а условию }V – пара мнимых корней, то есть наблюдается колебательная граница устойчивости.
Далее проводится определение устойчивости ДПТ по каждой из полученных четырех передаточных функций ДПТ (см. Табл. 3.5) при помощи критерия Гурвица.
По первой передаточной функции ДПТ (вход – напряжение, выход - частота) и по второй передаточной функции ДПТ (вход – момент сопротивления, выход - частота) характеристическое уравнение иссле-
дуемого объекта управления имеет вид: |
|
5,085 · 10VRx 2 6,592x 2 1,851 0. |
|
На основании уравнения |
(3.15) коэффициенты |0 примут вид: |
|: 5,085 · 10VR; |
| 6,592; | 1,851. |
Для устойчивости системы (объекта) второго порядка необходимо и достаточно, чтобы все коэффициенты ее характеристического полинома были положительными. Так как критерий Гурвица для исследуемого объекта управления выполняется, то можно сделать вывод, что рассматриваемый объект управления устойчив.
По третьей передаточной функции ДПТ (вход – напряжение, вы-
ход – |
угол поворота) и по четвертой передаточной функции ДПТ |
||
(вход – |
момент сопротивления, выход – |
угол поворота) |
характеристи- |
ческое уравнение исследуемого объекта управления имеет вид: |
|||
|
5,085 · 10VRxQ 2 6,592x 2 1,851x 0. |
|
|
На основании уравнения (3.15) коэффициенты |0 примут вид: |
|||
|: 5,085 · 10VR; | 6,592; |
| 1,851; |
|Q 0. |
|
Для устойчивости системы (объекта) третьего порядка необходимо и достаточно, чтобы при всех положительных коэффициентах ее
-36-
характеристического полинома, второй определитель матрицы Гурвица был положительным. | 0
В рассматриваемом случае коэффициент Q , а все остальные коэффициенты имеют положительный знак. Следовательно, при условии положительности второго определителя матрицы Гурвица, исследуемый объект будет находиться на границе апериодической устойчи-
вости. |
|
|
|
|
|
|
|
Так как справедливо неравенство |
|
· 1,851 „ 9,4 · 10 |
|
… 0 |
|
||
∆ ƒ|: |
| |
ƒ | | 6 |Q|: 5,085 · 10 |
VR |
VR |
|
||
| |
|Q |
|
|
|
, |
||
то исследуемый объект находится на границе апериодической устойчивости.
3.7.2. Частотный критерий устойчивости Михайлова
Критерий Михайлова был сформулирован и обоснован в 1936 г. российским ученым А. В. Михайловым. Позднее германские специалисты А. Леонард и Л. Кремер независимо от Михайлова сформулировали аналогичный критерий, поэтому в западной литературе он получил название критерия Михайлова-Леонарда-Кремера.
Критерий Михайлова так же, как и критерий Гурвица, основан на анализе характеристического уравнения системы, и поэтому с его помощью можно судить об устойчивости и замкнутых, и разомкнутых систем.
Пусть левая часть характеристического уравнения (характеристи-
ческий полином) системы управления имеет вид: |
|
|
|
||||||
†<x= |:x} |
2 | x}V 2 ~ 2 |}V x 2 |}. |
|
|||||||
Пусть будет выполнена замена переменных |
p jω. |
Тогда полу- |
|||||||
чится функция комплексного переменного: |
|
|
|||||||
†<Š = | |
<Š = |
} |
2 | <Š = |
}V |
2 ~ 2 | |
}V |
Š 2 | |
||
: |
|
|
|
|
}. |
||||
Ее можно так же, как амплитудно-фазовую частотную характери-
стику, представить в виде суммы действительной и мнимой частей: |
|||
†<Š = ‹< = 2 ŠŒ< = |
четные степени пе- |
||
Действительная часть |
‹< = |
содержит только. |
|
ременного ω: |
|
|
|
<‹<= = |: } 2 | }V 2 ~ 2 |}
а мнимая часть Œ только нечетные ,
Œ< = – | 2 | : 2 ~ 2 |
}V Q }VQ }V .
-37-
|
Каждому фиксированному значению переменного |
|
соответст- |
|||||||||||
вует комплексное число, которое можно изобразить в |
виде вектора на |
|||||||||||||
|
|
|
|
|||||||||||
ся |
|
|
|
†<Š = |
|
|
|
|
|
|
|
|
от 0 до ∞, |
|
комплексной плоскости. Если теперь изменять параметр |
|
|||||||||||||
|
|
|
|
|
опишет некоторую кривую, |
которая называет- |
||||||||
то конец вектора |
|
|
|
|
|
|
||||||||
|
характеристической кривой, или годографом Михайлова. По виду |
|||||||||||||
этой кривой можно судить об устойчивости системы. |
|
|
|
|
||||||||||
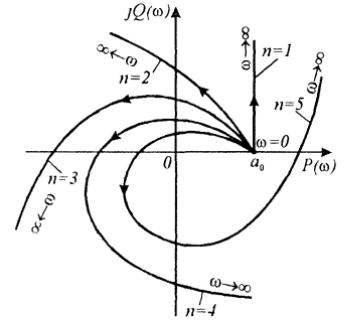
|
Формулировка критерия Михайлова: линейная динамическая сис- |
|||||||||||||
повернется |
|
|
|
|
|
|
|
|
|
|
|
|
†<Š = |
|
тема, описываемая уравнением -го порядка, будет устойчивой, если |
||||||||||||||
при этом в нуль (см. Рис. 3.3). |
|
,•/2 |
|
|
|
|
|
|
||||||
|
|
|
|
от 0 до ∞ |
характеристический вектор системы |
|
||||||||
при изменении |
|
|
, |
|
, нигде не обращаясь |
|||||||||
|
|
против часовой стрелки на угол |
|
|||||||||||
Рис. 3.3. Годографы Михайлова устойчивых систем.
Далее проводится определение устойчивости ДПТ по каждой из полученных четырех передаточных функций ДПТ (см. Табл. 3.5) при помощи критерия Михайлова.
По первой передаточной функции ДПТ (вход – напряжение, выход – частота) и по второй передаточной функции ДПТ (вход – момент сопротивления, выход – частота) характеристический полином иссле-
дуемого объекта управления имеет вид
†<x= 5,085 · 10VRx 2: 6,592x 2 1,851.
После замены переменных x Š получится функция комплексного переменного:
-38-
†<Š = 5,085 · 10VR<Š = 2 6,592Š 2 1,851.
После разложения в сумму действительной и мнимой частей по-
лучится выражение
†<Š = ‹< = 2:ŠŒ< = Ž1,851 6 5,085 · 10VR • 2 ŠŽ6,592 •.
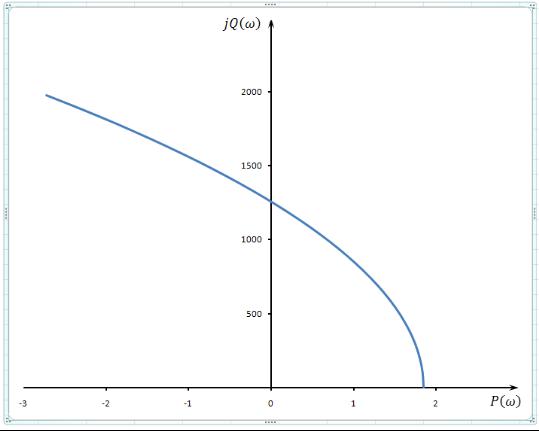
По найденным действительной и мнимой частям функции комплексного переменного строится годограф Михайлова. Результат его построения в среде MathCad приведен на Рис. 3.4.
Рис. 3.4. Годограф Михайлова для первой и второй передаточных функций.
Из годографа следует, что рассматриваемый объект управления устойчив.
По третьей передаточной функции ДПТ (вход – напряжение, выход – угол поворота) и по четвертой передаточной функции ДПТ (вход – момент сопротивления, выход – угол поворота) характеристи-
ческий полином исследуемого объекта управления имеет вид
†<x= 5,085 · 10VRxQ 2 6,592x 2 1,851x. :
-39-
После замены переменных x Š получится функция комплекс-
ного переменного
†<Š = :5,085 · 10VR<Š =Q 2 6,592<Š = 2 1,851Š .
После разложения в сумму действительной и мнимой частей по-
лучится выражение
†<Š = ‹< = 2 ŠŒ: < = Ž66,592 • 2 ŠŽ1,851 6 5,085 · 10VR Q•.
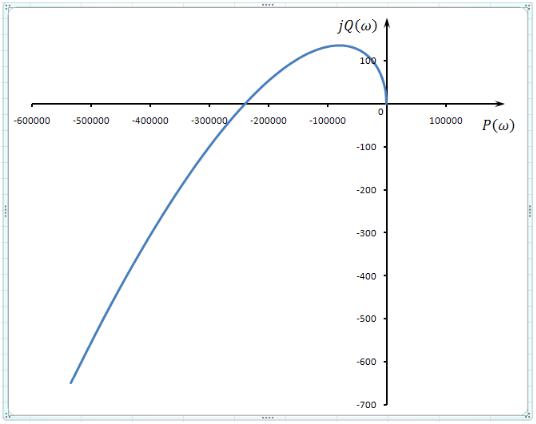
По найденным действительной и мнимой частям функции комплексного переменного строится годограф Михайлова. Результат его построения в среде MathCad приведен на Рис. 3.5.
Рис. 3.5. Годограф Михайлова для третьей и четвертой передаточных функций.
Из рисунка видно, что годограф Михайлова начинается в начале координат. Это означает, что в характеристическом уравнении исследуемого объекта имеется, по крайней мере, один нулевой корень. Следовательно, рассматриваемый объект управления находится на границе апериодической устойчивости.
-40-
