Вычисление ранга матрицы.

Метод окаймляющих миноров нахождения ранга матрицы.

Определение. Минор М матрицы А называется окаймляющим для минора М, если он получается из последнего добавлением одной новой строки и одного нового столбца матрицы А. Т.о. порядок окаймляющего минора М на единицу больше порядка минора М.

Теорема 7. (доказательство следует из теоремы о базисном миноре). Если для некоторого минора матрицы все окаймляющие миноры равны нулю, то он является базисным.

1. Найти какой-нибудь минор М₁ 1-го порядка (т.е. элемент матрицы), отличный от нуля. Если такого минора нет, то матрица А нулевая и r(A)=0.

2. Вычислять миноры 2-го порядка, содержащие М₁ (окаймляющие миноры) до тех пор, пока не найдется минор М₂, отличный от нуля. Если такого минора нет, то r(A)=1, если есть, то r(A)≥2.

………………

k) Вычислять (если они существуют) миноры k-го порядка, окаймляющие минор M_k-1≠0. Если таких миноров нет, то r(A)=k-1; если есть хотя бы один такой минор, то M_k≠0 r(A)≥k, и процесс продолжается.

Пример. Найдем r(A). А=. Т.к. есть ненулевые элементы, то r(A)≥1. Найдем ненулевой минор 2-го порядка. Например, М₂=.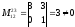

Значит, r(A)≥2. Вычислим миноры 3-го порядка, окаймляющие этот минор. 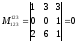,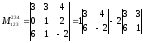=-30+30=0.

Все миноры 3-го порядка, окаймляющие М₂ равны нулю, следовательно, r(A)<3,т.е. r(A)=2. 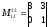- один из базисных миноров.

Метод элементарных преобразований нахождения ранга матрицы:

Матрицу А приводят к ступенчатому виду с помощью элементарных преобразований. Количество ненулевых строк полученной ступенчатой матрицы есть искомый ранг матрицы. Пример. Найти ранг матрицы методом элементарных преобразований.

Полученная матрица имеет 2 ненулевые строки, значит ее ранг равен 2. Следовательно, ранг исходной матрицы равен 2. Замечание. Если а₁₁=0, то перестановкой строк или столбцов добиваемся того, чтобы а₁₁≠0.

Системы линейных алгебраических уравнений (слау).

В общем случае система m линейных уравнений с n неизвестными (линейная система) имеет следующий вид:

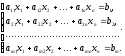(1)

Где х₁,х₂,…,х_n-неизвестные, а₁₁,а₁₂,…,а_mn – коэффициенты системы, b₁,b₂,…,b_m – свободные члены.

У коэффициентов a_ij i-номер уравнения, j-номер неизвестного, при котором стоит этот коэффициент.

Если все свободные члены b₁,b₂,…,b_m равны 0, то система (1) называется однородной. Если хотя бы один из b₁,b₂,…,b_m отличен от 0, система (1) - неоднородная.

Система (1) называется квадратной, если m=n.

Решением системы (1) называется такая совокупность n чисел с₁,с₂,…,с_n, которая при подстановке в систему вместо неизвестных х₁,х₂,…,х_n обращает все уравнения системы в тождество.

СЛАУ можно записать в виде (i=1,2,…,m) (2)

Система уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет ни одного решения.

Совместная система называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения.

СЛАУ

Пример. несовместная система.

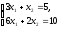-неопределенная (х₁=с, х₂=5-3с)

Две системы уравнений называются эквивалентными, или равносильными, если имеют одно и то же множество решений.

Запишем систему уравнений в матричной форме.

А=(3) , Х=(4) , В=(5)

Где А- матрица системы, Х- матрица-столбец переменных, В- матрица-столбец свободных членов.

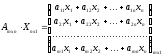- матрица-столбец.

Элементы этой матрицы-левые части системы (1). Т.о. систему можно записать в матричном виде: АХ=В (6)

-А^* = (А|В) расширенная матрица системы (1)

Решение матричного уравнения (6) заключается в отыскании такого столбца (4), который при заданной матрице (3) и заданном столбце (5) обращает уравнение (6) в тождество.

Систему (1) можно записать и в векторной форме:

х₁+х₂+…+х_n=

Или, обозначая столбцы соответственно a₁,…,a_n,В

a₁x₁+…+a_nx_n=В (7)

Т.о., решение СЛАУ можно трактовать как представление столбца В в виде линейной комбинации столбцов a₁,…,a_n.

Т.о., в отношении системы (1) мы должны научиться устанавливать следующие факты:

1) является ли система (1) совместной;

2) является ли система (1) (в случае ее совместности) определенной или нет;

3) способ отыскания единственного решения совместной системы (1) (в случае ее определенности) и отыскания всех ее решений (в случае ее неопределенности).

Теорема Крόнекера-Капелли (Леопольд Кронекер (1823-1891) – немецкий математик, Альфред Капелли (1855-1910) – итальянский математик). Для того, чтобы система линейных уравнений (1) являлась совместной, необходимо и достаточно, чтобы ранг ее матрицы был равен рангу расширенной матрицы этой системы.

Доказательство. Необходимость. Пусть r=rgA rr(AВ). Поэтому достаточно показать, что ранг матрицы А не меньше ранга ее расширенной матрицы, т.е. rr(AВ). Пусть система (1) совместна.

Это означает, что столбец В=в расширенной матрице системе является линейной комбинацией остальных столбцов. Выберем какой-либо базисный минор матрицы А. Без ограничения общности, пусть он будет расположен в верхнем левом углу, т.е. М_r=.

По теореме о базисном миноре, базисные столбцы линейно независимы, в то время как j>k существуют такие числа _ijR, i=1,2,…,k a_j=_1ja₁+_2ja₂+…+_rja_r,

Где a_j – j-й столбец матрицы А.

Тогда столбец b=a₁x₁+…+a_rx_r+a_r+1x_r+1+…+a_nx_n=

=a₁x₁+…+a_rx_r+(_1,r+1a₁+_2,r+1a₂+…+_r,r+1a_r)x_r+1+…+(_1na₁+_2na₂+…+_{r n}a_r)x_n

Является линейной комбинацией базисных столбцов матрицы А. Это значит, что М_r является также базисным минором расширенной матрицы (AВ), т.к.

1) он ненулевой;

2) если взять какой-либо окаймляющий минор М, то либо он будет минором матрицы А, т.е. ненулевым, либо он будет содержать столбец В и, следовательно, не может быть ненулевым, т.к. его столбцы линейно зависимы. Поэтому rg (AВ)=rg A.

Достаточность. Пусть rg (AВ)=rg A. выберем в А базисный минор М. Тогда он будет базисным и в матрице (AВ). Значит, столбец В можно представить как линейную комбинацию базисных столбцов a₁,…,a_r:

В=a₁x₁+…+a_rx_r.

Полагая x_r+1=x_r+2=…=x_n=0, получаем решение x₁,…,x_n исходной СЛАУ, т.к.

В=a₁x₁+…+a_rx_r=a₁x₁+…+a_rx_r+0a_r+1+…+0a_n.

Это означает, что СЛАУ совместна. Ч.т.д.