Определитель суммы и произведения матриц.

Из линейного свойства определителя следует, что определитель суммы двух квадратных матриц одного и того же порядка n A=(a_ij) и B=(b_ij) равен сумме всех различных определителей порядка n, которые могут получиться, если часть строк (столбцов) брать совпадающими с соответствующими строками (столбцами) матрицы А, а остальную часть – совпадающими с соответствующими строками (столбцами) В.

Определитель произведения двух квадратных матриц равен произведению их определителей: , А и В – матрицы n–го порядка.

Из этого свойства следует, что даже если 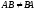, то.

Пример. Формулу для разложения определителя наиболее удобно использовать по тем строкам (столбцам), в которых большинство элементов равны 0.. Так, если в данной строке только один элемент отличен от нуля, то разложение по этой строке содержит только одно слагаемое и вопрос о вычислении определителя порядка n сводится к вычислению определителя порядка (n-1).

Вычислим следующий определитель, применяя свойства к столбцам.

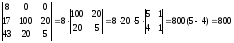
Обратная матрица.

Пусть А – квадратная матрица порядка n, а Е – единичная матрица того же порядка.

Матрица В называется правой обратной по отношению к матрице А, если АВ=Е.

Матрица С называется левой обратной по отношению к матрице А, если СА=Е.

Т.к. обе матрицы А и Е являются квадратными порядка n, то матрицы В и С (если они существуют) также являются квадратными матрицами порядка n.

Убедимся, что если обе матрицы В и С существуют, то они совпадают между собой на основании равенств АЕ=А, АВ=Е, СА=Е и сочетательного свойства произведения матриц: С=СЕ=С(АВ)=(СА)В=ЕВ=В.

Т.о., правая и левая обратные матрицы совпадают В=С=А^-1

Определение. Матрица А^-1 называется обратной по отношению к матрице А, если при умножении этой матрицы на данную как справа, так и слева получается единичная матрица: АА^-1=А^-1А=Е.

Если 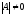, то матрица называетсяневырожденной, или неособенной. Если - матрица вырожденная, или особенная.

Но не каждая квадратная матрица имеет обратную. Если для существования числа а^-1, обратного для числа а, необходимым и достаточным условием является , то для существования А^-1 таким условием является .

Теорема 1 (критерий существования обратной матрицы). Квадратная матрица А имеет обратную матрицу тогда и только тогда (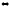), когда А невырожденная. Если обратная матрица существует, то она единственная.

Доказательство. Необходимость. Пусть матрица А имеет обратную матрицу А^-1. Покажем, что в этом случае А невырожденная.

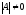АА^-1=А^-1А=Е. Тогда по свойству определителей имеем: . Т.е.и.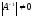

Достаточность. Пусть 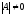. Покажем, что она имеет обратную матрицу.

Рассмотрим квадратную матрицу n-го порядка, которая называется присоединенной (взаимной, союзной), элементы которой равны алгебраическим дополнениям элементов матрицы А^Т: (i=1,2,…,n; j=1,2,…,n). Достаточно показать, что оба произведения С=А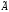 и В=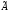·А являются единичной матрицей.

У обеих матриц С и В любой элемент, не лежащий на главной диагонали, равен нулю, т.к., например,

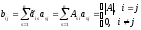
(по свойствам определителя ,а еслиi=j, то 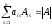представляет собой разложение определителя по строке).

Следовательно В (ровно как и С) – диагональная матрица, элементы главной диагонали равны определителю матрицы А: 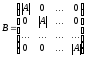. Аналогично для С=А·, т.е.·А=А·=В.

Значит, если в качестве обратной матрицы взять матрицу

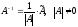, (2.2) то А·А^-1=А^-1·А=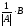=Е_n. ч.т.д.

Докажем единственность А^-1. Допустим, существуют еще матрицы С и D, такие, что и АС=Е, DA=E. Тогда, умножая на А^-1 первое из равенств, получаем А^-1АС=А^-1Е. Отсюда ЕС=А^-1Е, т.е. С=А^-1 . Аналогично, умножая второе равенство (DА=Е) на А^-1 справа получаем D=А^-1 . ч.т.д.

Т.о. , где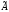-присоединенная матрица , Элементы которой равны алгебраическим дополнениям элементов матрицы А^Т.

Терема 2. Если квадратные матрицы А и В порядка n имеют обратные матрицы, то и их произведение имеет обратную матрицу, причем (АВ)^-1=В^-1А^-1.

Доказательство. Достаточно доказать, что (АВ)(В^-1А^-1)=Е и (В^-1А^-1)(АВ)=Е.

По свойству ассоциативности умножения матриц имеем:

(АВ)(В^-1А^-1)=А(ВВ^-1)А^-1=АЕА^-1=АА^-1=Е,

(В^-1А^-1)(АВ)=В^-1(А^-1А)В=В^-1ЕВ=Е. ч.т.д.

Теорема 3. Если матрица А порядка n имеет обратную, то и транспонированная матрица А^Т имеет обратную, причем (А^Т)^-1=(А^-1)^Т.

Доказательство. Достаточно доказать, что А^Т(А^Т)^-1=Е и (А^Т)^-1А^Т=Е.

Используя свойства произведения матриц относительно операции транспонирования, имеем:

А^Т(А^Т)^-1=(А^-1А)^Т=Е^Т=Е,

(А^Т)^-1А^Т=(АА^-1)^Т=Е^Т=Е ч.т.д.