Определители.

Каждой квадратной матрице поставим в соответствие определенную числовую характеристику, называемую определителем , соответствующим этой матрице. Обозначение: .

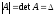1. Порядок n матрицы А равен 1. Тогда А=(а₁₁) и .

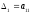2. Определителем матрицы второго порядка, или определителем второго порядка, называется число:

. (4) Пример.

3. Определителем матрицы третьего порядка, или определителем третьего порядка, называется число:

(5)

Знаки, с которыми члены определителя входят в формулу (5) запоминаются при помощи схемы, которая называется формулой треугольника или правилом Сарруса.

Пример. 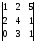=27

Определители более высокого порядка.

Введем понятия перестановок и инверсий.

Пусть каждое из чисел ₁,₂,…,_n принимает одно из значений 1,2,…,n, причем среди этих чисел нет совпадающих. В таком случае говорят, что числа ₁,₂,…,_n являются некоторой перестановкой чисел 1,2,…,n. Образуем из чисел ₁,₂,…,_n все возможные пары _i_j. Будем говорить, что пара _i_j образует инверсию, если _i>_j, т.е. бóльшее число предшествует меньшему. Например, в перестановке J=(2,3,1) одна инверсия (3,1), а в перестановке (4,3,2,1) – 4 инверсии: (4,3), (3,2), (2,1). Обозначим через r(J) количество инверсий в перестановке J.

Рассмотрим квадратную матрицу A порядка n. Выберем из общего числа n² элементов матрицы набор, содержащий n элементов, таким образом, чтобы в него входило по одному элементу из каждой строки и каждого столбца. Например, наборы элементов главной (а₁₁, а₂₂, …, а_nn) и побочной (а_n1, а_n-12, …, а_1n) диагонали.

Каждый такой набор можно упорядочить, записав сначала элементы 1-й строки, затем из 2-й и т.д., т.е. .

Номера столбцов (j₁, j₂,…,j_n) образуют перестановку J из n чисел 1,2,…,n. Всего существует n!=1·2·…·n (“эн” факториал) различных перестановок из n натуральных чисел.

Введем понятие инверсии в перестановке J. Это наличие пары чисел, в которой бóльшее число предшествует меньшему. Например, в перестановке J=(2,3,1) одна инверсия (3,1), а в перестановке (4,3,2,1) – 4 инверсии: (4,3), (3,2), (2,1). Обозначим через r(J) количество инверсий в перестановке J.

Каждому набору 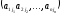поставим в соответствие произведение его элементови число r(J), равное количеству инверсий в перестановке J=(j₁,j₂,…,j_n) из номеров соответствующих столбцов.

Определение. Определителем квадратной матрицы n-го порядка, или определителем n-го порядка, называется число, равное алгебраической сумме n! членов, каждый из которых является произведением n элементов матрицы, взятых по одному из каждой строки и каждого столбца, причем знак каждого члена определяется как (-1)^r(J), где r(J)-число инверсий в перестановке J из номеров столбцов элементов матрицы, если при этом номера строк записаны в порядке возрастания:

(6)

где сумма берется по всем перестановкам J.

Пример. При n=3 получаем

Δ₃=

Т.е. тоже число, что и по формуле (5).

Но с ростом n резко растет число n!. Так при n=4 число слагаемых уже равно 24. Поэтому на практике часто используют другие формулы. Введем новые понятия.

Минором М_ij элемента 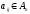называется определитель матрицы (n-1)-го порядка, полученной из матрицы А вычеркиванием i-й строки и j-го столбца.Пример.

Каждая матрица n-го порядка имеет n² миноров (n-1)-го порядка.

Алгебраическим дополнением элемента называется его минор, взятый со знаком (-1)^i+j. А_ij=(-1)^i+jM_ij. Пример.

Теорема. Определитель n-го порядка равен сумме произведений элементов любой строки (столбца) на их алгебраические дополнения:

Δ=a_i1A_i1+a_i2A_i2+…+a_inA_in=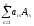- разложение по элементам i-й строки.(7)

Δ=a_1jA_1j+a_2jA_2j+…+a_njA_nj=- разложение по элементам j-го столбца.(8)

Доказательство (Б.д.) (с. 19).

Вычислим так называемый треугольный определитель, у которого все элементы ниже главной диагонали равны 0. Разложим его по 1-му столбцу:

.

Определитель Δ_n-1 так же раскладываем по 1-му столбцу, Получаем треугольный определитель Δ_n-2 (n-2)-го порядка, и т.д..В результате аналогичных рассуждений, получаем Δ_n=а₁₁а₂₂…а_nn. Для треугольного определителя, у которого все элементы выше главной диагонали равны нулю, и для диагональной матрицы получаем те же результаты. Т.о. определитель треугольной и диагональной матриц равен произведению элементов на главной диагонали. Пример.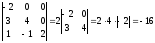

Теорема Лапласа.

Пусть k<n, а i₁,i₂,…,i_k и j₁,j₂,…,j_k – произвольные номера, удовлетворяющие условиям 1 i₁<i₂<…<i_kn и 1 j₁<j₂<…<j_kn.

Определение. Минором k-го 1-го типа порядка матрицы А называется определитель k-го порядка с элементами, лежащими на пересечении k строк с номерами i₁,i₂,…,i_k и любых k столбцов с номерами j₁,j₂,…,j_k матрицы А. (k≤min(m,n)). .

Пример. , миноры 1-го порядка: =,=;

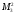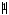миноры 2-го поря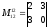дка: , 3-го порядка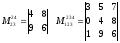

Определение. Минором k-го 2-го типа порядка матрицы А называется определитель порядка n-k, соответствующий матрице, полученной из матрицы А в результате вычеркивания любых k строк с номерами i₁,i₂,…,i_k и любых k столбцов с номерами j₁,j₂,…,j_k матрицы А. (k≤min(m,n)). .

Пример.

Теорема Лапласа. При любом номере k<n, и при любых фиксированных номерах строк i₁,i₂,…,i_k таких, что 1 i₁<i₂<…<i_kn, для определителя n-го порядка, справедлива формула:

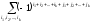
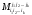
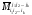= (9)

Разложение определителя по k строкам i₁,i₂,…,i_k. Суммирование в этой формуле идет по всевозможным значениям индексов j₁,j₂,…,j_k, удовлетворяющие условиям 1 j₁<j₂<…<j_kn.

Формула (9) является обобщением формулы (7). (Доказательство с. 25).