Свойства определителей

1. При транспонировании матрицы ее определитель не изменяется: .

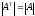Это свойство вытекает из теоремы о разложении определителя . Т.к. разложение определителя 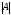по 1-му столбцу тождественно совпадает с разложениемпо 1-й строке.

Это свойство означает полную равноправность строк и столбцов и позволяет все последующие свойства устанавливать лишь для строк, подразумевая, что они справедливы и для столбцов.

2. Свойство антисимметрии при перестановке двух строк (столбцов).

При перестановке двух строк (столбцов) матрицы ее определитель меняет знак на противоположный.

Доказательство. Допустим сначала, что переставлены две соседние строки матрицы: i и i+1. Разложим определитель исходной матрицы Δ по элементам i-й строки, а определитель новой матрицы Δ^΄ - по элементам (i+1)-й строки. Разложения будут отличаться только знаком, т.к. в разложении определителя Δ^΄ каждое алгебраической дополнение A_i+1j будет иметь противоположный знак (множители (-1)^i+j сменятся на множители (-1)^i+1+j). Т.о. Δ^=-Δ^΄.

Если переставить не соседние строки, а, например, i-ю и (i+m)-ю, то эту перестановку можно рассматривать как последовательное смещение i-й строки на m строк вниз (при этом каждый раз знак определителя меняется), а (i+m)-й строки на (m-1) вверх и (m-1) раз меняется знак, т.е. знак поменяется нечетное число раз: (m+m-1=2m-1). Следовательно, Δ =-Δ^΄.

Для столбцов доказательство аналогично.

3. Линейное свойство определителя.

Некоторая строка а=(а₁,а₂,…,а_n) называется линейной комбинацией строк b=(b₁,b₂,…,b_n), c=(c₁,c₂,…,c_n),…, d=(d₁,d₂,…,d_n), с коэффициентами λ₁,λ₂,…,λ_k если она равна сумме произведений этих строк на эти числа:

a=λ₁b+λ₂c+…+λ_kd, т.е. a_j=λ₁b_j+λ₂c_j+…+λ_kd_j j=1,2,…,n

Если в определителе n-го порядка  некоторая i-я строка (a_i1,a_i2,…,a_in) является линейной комбинацией строк (b_i1,b_i2,…,b_in) и (c_i1,c_i2,…,c_in) с коэффициентами  и , то =₁+₂, где ₁ – определитель, у которого i-я строка равна (b_i1,b_i2,…,b_in), а все остальные строки такие же, как и у , а где ₂ – определитель, у которого i-я строка равна (с_i1,с_i2,…,с_in), а все остальные строки такие же, как и у .

=+

Доказательство. Разложим каждый из определителей , ₁, и ₂ по i-й строке по формуле Δ=a_i1A_i1+a_i2A_i2+…+a_inA_in=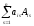.Заметим, что алгебраические дополнения A_ij i-й у всех 3-х определителей одинаковы. Следовательно, формула =₁+₂ следует из равенств a_j=λb_j+c_j j=1,2,…,n ч.т.д.

Замечание. Линейное свойство справедливо и для случая, когда i-я строка является линейной комбинацией не 2-х, а нескольких строк.

Рассмотренные 3 свойства являются основными свойствами определителя. Следующие 5 свойств являются логическими следствиями этих свойств.

4. Определитель с двумя одинаковыми строками (столбцами), то равен 0.

Док-во. Переставим равные строки (столбцы) местами. С одной стороны, определитель не изменится, а с другой, по св-ву 2, поменяет знак. Т.е. Δ=-Δ, след-но, Δ=0.

5. Если все элементы какой-либо строки (столбца) определителя умножить на число λ, то и определитель умножится на это число λ.

Доказательство. Вытекает из свойства 3 при =0. Ч.т.д.

Замечание. Т.о., за знак определителя можно выносить общий множитель любой строки или столбца в отличие от матрицы, за знак которой можно выносить только общий множитель всех элементов.

Пример. 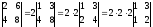, но

6. Если все элементы некоторой строки (столбца) определителя равны 0, то и сам определитель равен 0.

Доказательство. Это свойство следует из свойства 5 при =0. ч.т.д.

7. Если элементы двух строк (столбцов) определителя пропорциональны, то определитель равен 0.

Доказательство. По свойству 5 коэффициент пропорциональности λ можно вынести за знак определителя, после чего останется определитель с двумя одинаковыми строками: Δ^΄=λΔ, где Δ имеет две одинаковые строки и по свойству 4 равен 0. ч.т.д.

8. Определитель не изменится, если к элементам какой-либо строки (столбца) матрицы прибавить элементы другой строки (столбца), предварительно умноженные на одно и то же число.

Доказательство. Полученный в результате указанного прибавления определитель, по свойству 3, можно разбить на сумму двух определителей, один из которых равен исходному, а второй равен 0 в силу пропорциональности двух строк (столбцов) и свойства 7.: =+0. ч.т.д.

9. Свойство алгебраических дополнений соседних строк (столбцов).

Сумма произведений элементов какой-либо строки (столбца) определителя на соответствующие алгебраические дополнения элементов другой строки (столбца) этого определителя равна 0, т.е. .

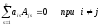Доказательство. Докажем для строк (для столбцов доказательство аналогично). Запишем разложение определителя  по i-й строке:

Δ==a_i1A_i1+a_i2A_i2+…+a_inA_in (7)

Т.к. алгебраические дополнения A_i1, A_i2,…,A_in не зависят от элементов i-й строки a_i1,a_i2,…,а_in, то равенство (70 является тождеством относительно a_i1,a_i2,…,а_in и сохраняется при замене чисел a_i1,a_i2,…,а_in любыми другими n числами. Заменив a_i1,a_i2,…,а_in соответствующими элементами любой (отличной от i-й) k-й строки a_k1,a_k2,…,а_kn, получим слева в (7) определитель с двумя одинаковыми строками a_k1,a_k2,…,а_kn, равный нулю по свойству 4. Таким образом:

a_k1A_i1+a_k2A_i2+…+a_knA_in=0 ik. Ч.т.д.

10. Сумма произведений произвольных чисел с₁,с₂,…,с_n на алгебраические дополнения элементов любой строки (столбца) равна определителю матрицы. Полученной из данной заменой элементов этой строки (столбца) на числа с₁,с₂,…,с_n.

Свойство также следует из формулы (7).