
- •1.Информатика как предмет. Основные направления и научные формирования.
- •2.Понатие алгоритма и его свойства. Пример – алгоритм перемножения двух целых чисел.
- •3.Средства описания алгоритмов. Примеры.
- •4. Языки программирования
- •5.Кодирование данных двоичным кодом.
- •6.Язык Паскаль. Типы данных в языке Паскаль.
- •7.Стандартные функции языка Паскаль
- •9.Основные операторы Паскаля и типовая структура Паскаль – программы.
- •10. Разветвляющиеся алгоритмы. Условные операторы в Паскале
- •11.Циклические алгоритмы. Оператор цикла с параметром.
- •12.Циклические алгоритмы. Оператор цикла с предусловием.
- •13.Циклические алгоритмы. Оператор цикла с постусловием
- •14.Массивы в Паскале. Основные алгоритмы обработки одномерных массивов.
- •15.Ввод и вывод массивов через файлы. Пример – вывод в файл двух матриц рядом.
- •16. Подпрограмма – функция. Пример: возведение вещественного числа в целочисленную степень.
- •17.Подпрограмма-процедура. Пример – решение треугольной слау.
- •18.Параметры-значения и параметры-переменные.
- •19.Метод половинного деления
- •20.Алгоритм метода половинного деления.
- •21.Метод простой итерации для поиска корней. Геометрическая интерпретация.
- •22. Приведение уравнения к виду, пригодному для применения метода итераций.
- •23.Общая оценка погрешности приближения к корню.
- •24.Оценка погрешности приближения в методе простой итерации.
- •25. Метод Ньютона
- •26.Модификация метода Ньютона и оценки погрешности приближения.
- •27.Метод хорд и оценка погрешности приближения в методе хорд.
- •28.Понятие нормы. Нормы векторов в конечномерном пространстве.
- •29. Нормы матриц. Согласованность и подчиненность норм.
- •31. Метод прогонки для решения систем линейных алгебраических уравнений.
- •32. Метод простой итерации для решения систем линейных алгебраических уравнений
- •33.Сходимость последовательности векторов и матричной прогрессии
- •34.Сходимость Метода Простых Итераций для решения систем линейных уравнений.
- •35.Оценки погрешности метода простой итерации для решения систем линейных алгебраических уравнений.
- •36.Метод Зейделя для решения систем линейных алгебраических уравнений.
- •37. Приведение метода Зейделя к методу простой итерации.
- •38. Метод последовательной внешней (верхней) релаксации
- •39.Постановка задачи интерполирования.
- •40.Алгебраическое интерполирование
- •42.Свернутая форма полинома Лагранжа.
- •43. Погрешность алгебраического интерполирования.
- •44.Интерполирование сплайнами
- •45.Метод наименьших квадратов .
где 1-наибольшое собств значение симметричной матрицы AA, являющейся произведением транспонированной и исходной матриц. Т к матрица AA симметричная, то все ее собственные значения вещественны и положительны. Число -собств значение, а ненулевой вектор x – собственный вектор матрицы A(если они связаны между собой соотношением Ax=x). Если же матрица A сама является симметричной, A = A, то AA = A2 и тогда 1 =
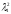 ,
где
,
где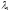 - наибольшее по модулю собственное
значение матрицыA.
Следовательно, в этом случае мы имеем
- наибольшее по модулю собственное
значение матрицыA.
Следовательно, в этом случае мы имеем
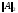 =
=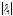 .
.Собственные числа матрицы не превышают любой из ее согласованных норм. Нормируя определяющее собственные числа соотношение, получим ||λx||=||Ax||, |λ|·||x||=||Ax||||A||·||x||, |λ|||A||
Поскольку справедливо ||A||2||A||e, где евклидова норма вычисляется просто, в оценках вместо спектральной нормы можно использовать евклидову норму матрицы.
30.Обусловленность систем уравнений. Коэффициент обусловленности.
Степень обусловленности - влияние решения на исходные данные. Ax = b : вектору b соответствует решение x. Пусть b изменится на величину
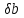 .
Тогда векторуb+
.
Тогда векторуb+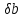 будет соответствовать новое решение
x+
будет соответствовать новое решение
x+ :A(x+
:A(x+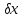 )
=b+
)
=b+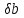 .
Так как система линейна, то Ax
+ A
.
Так как система линейна, то Ax
+ A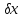 = b+
= b+ ,
тогда A
,
тогда A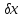 =
=
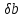 ;
;
 =
=
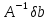 ;
;
 =
=

 ;b
= Ax;
;b
= Ax;
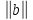 =
=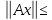
 тогда
тогда
 ;
;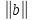
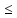

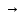
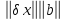
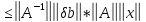
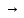

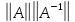 *
* ,
где
,
где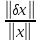 - относительная погрешность возмущения
решения,
- относительная погрешность возмущения
решения, –коэффициент
обусловленности cond(A)
(во сколько раз может возрасти погрешность
решения),
–коэффициент
обусловленности cond(A)
(во сколько раз может возрасти погрешность
решения),
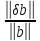 – относительное возмущение вектораb.
cond(A)
=
– относительное возмущение вектораb.
cond(A)
=
 ;
;

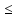 cond(A)*
cond(A)* Свойства
коэффициента: зависит от выбора нормы
матрицы; cond(
Свойства
коэффициента: зависит от выбора нормы
матрицы; cond(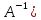 =cond(A);
умножение матрицы на число не влияет
на коэффициент обусловленности. Чем
больше коэффициент, тем сильнее
сказывается на решении СЛАУ ошибка в
исходных данных. Число обусловленности
не может быть меньше 1.
=cond(A);
умножение матрицы на число не влияет
на коэффициент обусловленности. Чем
больше коэффициент, тем сильнее
сказывается на решении СЛАУ ошибка в
исходных данных. Число обусловленности
не может быть меньше 1.31. Метод прогонки для решения систем линейных алгебраических уравнений.
Часто возникает необходимость в решении систем, матрицы которых, являясь слабозаполненными, т.е. содержащими много ненулевых элементов. Матрицы таких систем обычно имеют определенную структуру, среди которых выделяют системы с матрицами ленточной структуры, т.е. в них ненулевые элементы располагаются на главной диагонали и на нескольких побочных диагоналях. Для решения систем с ленточными матрицами метод Гаусса можно трансформировать в более эффективные методы. Рассмотрим наиболее простой случай ленточных систем, к которым, как мы увидим впоследствии, сводится решение задач дискретизации краевых задач для дифференциальных уравнений методами конечных разностей, конечных элементов и др. Трёх диагональной матрицей называется такая матрица, у которой ненулевые элементы стоят только на главной диагонали и соседних с ней:
У трёх диагональной матрицы ненулевых элементов всего (3n-2).
Переобозначим коэффициенты матрицы:
.
Тогда в покомпонентной записи систему можно представить в виде:
ai * xi-1 + bi * xi + ci * xi+1 = di , i1, 2,…, n; (7)

a1=0, cn=0. (8)
Структура системы предполагает взаимосвязь только между соседними неизвестными:
xi=i *xi+1+i (9)
Уменьшим в представлении (9) индекс на единицу:
xi-1=i-1*xi + i-1 и подставим в (7):
ai(i-1*xi + i-1)+ bi * xi + ci * xi+1 = di
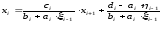
(ai *i-1 + bi )xi = –ci * xi+1 +di –ai * i-1
Сравнивая полученное выражение с представлением (7), получаем:
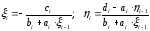
 (10)
(10)
Формулы (10) представляют рекуррентные соотношения для вычисления коэффициентов прогонки. Они требуют задания начальных значений. В соответствии с первым условием (8) для i =1 имеем a1=0, а значит
 ,
,
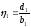 .
.Далее вычисляются и сохраняются остальные прогоночные коэффициенты по формулам (10) для i=2,3,…, n, причем при i=n, с учетом второго условия (8), получаем n=0. Следовательно, в соответствии с формулой (9) xn = n.
После чего по формуле (9) последовательно находятся неизвестные xn-1, xn-2, …, x1. Этот этап расчета называется обратным ходом, в то время как вычисление прогоночных коэффициентов называется прямым ходом прогонки.
Для успешного применения метода прогонки нужно, чтобы в процессе вычислений не возникало ситуаций с делением на нуль, а при большой размерности систем не должно быть быстрого роста погрешностей округления. Будем называть прогонку корректной, если знаменатель прогоночных коэффициентов (10) не обращается в ноль, и устойчивой, если i<1 при всех i=1,2,…, n. Достаточные условия корректности и устойчивости прогонки, которые во многих приложениях выполняются, определяются теоремой.
Теорема. Пусть коэффициенты ai и ci уравнения (7) при i=2,3,..., n-1 отличны от нуля и пусть
bi>ai+ci при i=1, 2,..., n. (11)
Тогда прогонка, определяемая формулами (10), (9) корректна и устойчива.
32. Метод простой итерации для решения систем линейных алгебраических уравнений
Альтернативой прямым методам решения СЛАУ являются итерационные методы, основанные на многократном уточнении
 ,
заданного приближенного решения системы
,
заданного приближенного решения системы .
Верхним индексом в скобках здесь и
далее по тексту обозначается номер
итерации (совокупности повторяющихся
действий).
.
Верхним индексом в скобках здесь и
далее по тексту обозначается номер
итерации (совокупности повторяющихся
действий).Как уже было сказано, в итерационных методах определяется не само решение задачи Ax=b, а некоторая последовательность векторов x(k) (k - номер итерации), такая, что она стремится к ветору решения при k. Чтобы построить такую последовательность, надо прежде всего исходную систему Ax=b преобразовать к виду
x=Bx+f. (12)
Сделать это можно различными способами. Самый простой и распространенный – это выражение каждого диагонального неизвестного из соответствующего по номеру уравнения системы:

т.е. преобразованные матрица B и вектор f имеют вид
 ,
f=
,
f= .
.Задаваясь начальным приближением – вектором x(0)=(x1(0), x1(0),…., x1(0),), получаем
 (13)
(13)Такая формула вычисления приближений определяет метод простой итерации – МПИ. Основной вопрос – будет ли последовательность векторов x(k) сходится к решению системы линейных уравнений. Итерации прерываются при выполнении условия
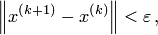 где
где —
заданная точность, которую необходимо
достигнуть при решении задачи.
—
заданная точность, которую необходимо
достигнуть при решении задачи.33.Сходимость последовательности векторов и матричной прогрессии
 …
… (1)
Сущ. сходимость по элементам и сходимость
по нормам.
(1)
Сущ. сходимость по элементам и сходимость
по нормам.Вектор
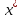 наз. пределом последовательности
векторов (1), если сущ. каждый изn
числовых пределов
наз. пределом последовательности
векторов (1), если сущ. каждый изn
числовых пределов
 i=1,2…..n
и
i=1,2…..n
и
 ,
,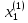 ….
….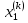 -
числовая последовательность(предел
-
числовая последовательность(предел )
Последовательность векторов (1) сходится
к вектору
)
Последовательность векторов (1) сходится
к вектору по норме,если предел
по норме,если предел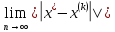 =0
=0В конечномерном пространстве сходимость по норме эквивалентна сходимости по компонентам.
Лемма Неймана. Условие, что все собственные числа матрицы<1 |
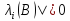 – необходимо и достаточно для того,
чтобы:
– необходимо и достаточно для того,
чтобы: и Е+B+
и Е+B+ +……+
+……+ +…..=(Е-В)^(-1)(обратная
матрица.
+…..=(Е-В)^(-1)(обратная
матрица.Лемма 2 Если норма ||B||< = q<1, то матрица (Е-B) имеет обратную, такую что Е+B+
 +……+
+……+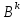 +…..=(Е-В)^(-1),
причем
|| (Е-В)^(-1)||<
=1/1-q
V=
Е+B+
+…..=(Е-В)^(-1),
причем
|| (Е-В)^(-1)||<
=1/1-q
V=
Е+B+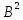 +……+
+……+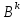 +….
+….||V||=||…||< =||E||+||B||+||
 ||+||+…+||+||
||+||+…+||+||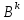 ||+…<||E||+||B||+||
||+…<||E||+||B||+||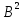 ||+||+…+||+||
||+||+…+||+|| ||<1+q+q^2+…q^n+…+1/1-q
||<1+q+q^2+…q^n+…+1/1-q||V||<=1/1-q
34.Сходимость Метода Простых Итераций для решения систем линейных уравнений.
Сходимость последовательности векторов x(0), x(1),…., x(k),…, определяют двумя способами: по компонентам и по норме.
Определение 1. Вектор x=(x1, x2,…., xn,) называется пределом этой последовательности векторов, если существует каждый из n числовых пределов
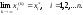 Определенная таким образом сходимость
называется сходимостью по компонентам.Определение 2.
Последовательность
векторов сходится к вектору x
по норме, если
Определенная таким образом сходимость
называется сходимостью по компонентам.Определение 2.
Последовательность
векторов сходится к вектору x
по норме, если
 .
.Сходимость по норме более общая, так как не зависит от того, будет ли векторное пространство конечной или бесконечной размерности. Если размерность имеет конечное значение n, то сходимость по норме и сходимость по компонентам равносильны (т.е. из одной следует другая). Сходимость по норме во многих случаях более удобна, чем сходимость по компонентам.
Все эти рассуждения распространяются и на последовательность матриц B(0), B(1), …, B(k), …, однако здесь нас будет интересовать последовательность степеней матриц E, B, B2, …, Bk, …, называемая матричной геометрической прогрессией.
Лемма Неймана. Условие, что все собственные числа матрицы<1 |
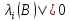 – необходимо и достаточно для того,
чтобы:
– необходимо и достаточно для того,
чтобы: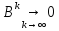 и Е+B+
и Е+B+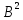 +……+
+……+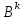 +…..=(Е-В)^(-1)(обратная
матрица.
+…..=(Е-В)^(-1)(обратная
матрица.Лемма 2 Если норма ||B||< = q<1, то матрица (Е-B) имеет обратную, такую что Е+B+
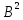 +……+
+……+ +…..=(Е-В)^(-1),
причем
|| (Е-В)^(-1)||<
=1/1-q
V=
Е+B+
+…..=(Е-В)^(-1),
причем
|| (Е-В)^(-1)||<
=1/1-q
V=
Е+B+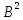 +……+
+……+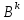 +….
+….||V||=||…||< =||E||+||B||+||
 ||+||+…+||+||
||+||+…+||+|| ||+…<||E||+||B||+||
||+…<||E||+||B||+|| ||+||+…+||+||
||+||+…+||+|| ||<1+q+q^2+…q^n+…+1/1-q
||<1+q+q^2+…q^n+…+1/1-q||V||<=1/1-q
Теорема 1 (о сходимости МПИ). Необходимым и достаточным условием сходимости МПИ при любом начальном векторе x(0) к решению x* СЛАУ x=Bx+f является требование, чтобы все собственные значения матрицы B по модулю были меньше единицы.
Докажем только достаточность.
Пусть собственные значения матрицы B по модулю были меньше единицы
maxi(B)<1, i=1,2,…, n. По лемме 1 имеем Bk при k, а также E + B + B2 + … + Bk + …= (E+B)-1.
Применяя последовательно формулу МПИ для вычисления приближений:
x(1)=Bx(0)+f,
x(2)=Bx(1)+f=B(Bx(0)+f)+f=B2x(0)+(E+B)f,
. . . . . . . . . .
x(k+1)=Bk+1x(0) + (E + B + B2 + … + Bk)f.
0 (
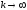 )
)Правая часть последнего выражения при любом x(0) и
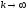 равна (E-B)-1f,
т.е. в пределе
равна (E-B)-1f,
т.е. в пределе
 .
.Представим исходную систему x=Bx+f в виде (E-B)x=f и подставим x*: (E-B)(E-B)-1f=f.
Получается, что x* действительно является решением системы уравнений.
Достаточность доказана.
Вспоминая соотношение между собственными значениями и нормами матриц, можно сформулировать достаточный признак устойчивости: Для сходимости МПИ достаточно, чтобы какая-либо норма матрицы B была меньше единицы.
Некоторые квадратные матрицы обладают свойством, называемым диагональным преобладанием. Это означает, что диагональные элементы по модулю больше суммы модулей всех остальных элемнтов в данной строке:
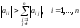 Для
изложенного способа преобразования
системы к итерационному виду справедливо
утверждение: в случае диагонального
преобладания в исходной матрице A
метод простой итерации сходится.
Для
изложенного способа преобразования
системы к итерационному виду справедливо
утверждение: в случае диагонального
преобладания в исходной матрице A
метод простой итерации сходится.35.Оценки погрешности метода простой итерации для решения систем линейных алгебраических уравнений.
Теорема о погрешностях. Пусть
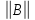
 q
q
 1, тогда справедливы оценки
1, тогда справедливы оценки
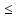

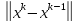 (1)
- апостериорная («после»).
(1)
- апостериорная («после»).
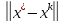
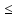
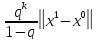 (2)
– априорная («до»). Док-во:
(2)
– априорная («до»). Док-во:
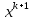 =B
=B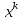 +f
+f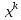 =
B
=
B +f
вычитаем нижнее из верхнего
+f
вычитаем нижнее из верхнего
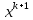 -
-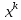 =B
=B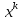 - B
- B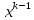 = B(
= B(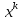 -
- );
);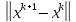 =
=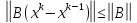 *
*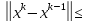 q*
q*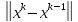 ;
;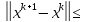 q*
q*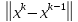 (**);
так как q<1,
то разности приближений и
(**);
так как q<1,
то разности приближений и

 0.
0.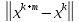 =
=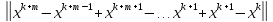
 +…+
+…+ +
+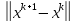
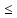 (заменим
каждую норму разности, используя(**))
(заменим
каждую норму разности, используя(**))
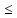 q*
q*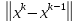 +
+ *
*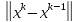 +…+
+…+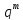 *
*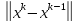 =q*(1+q+…+
=q*(1+q+…+ )*
)*
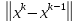 =q*
=q*
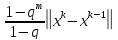 .Устремим m
к
.Устремим m
к
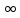 ,
фиксируя «k».
Тогда
,
фиксируя «k».
Тогда
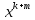
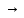
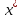 ,
,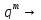 0, в результате чего получится соотношение(1).
По соотношению (**)
0, в результате чего получится соотношение(1).
По соотношению (**)
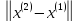
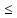 q*
q*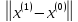 ;
;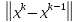

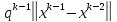 .
.36.Метод Зейделя для решения систем линейных алгебраических уравнений.
При вычислении очередного (k+1)-го приближения в МПИ в правую часть расчетной формулы (13) подставляется предыдущее, k-ое приближение, т.е. вектор x(k), все компоненты которого имеют одинаковый итерационный индекс: (x1(k), x2(k),…, xn(k)). Однако элементы вектора вычисляются последовательно, поэтому , например, при вычислении x2(k+1) уже вычислен x1(k+1) в новом приближении. Метод, в котором для подсчета i-ой компоненты (k+1)-ого приближения используются уже найденные на этом, т.е. (k+1)-м шаге, новые значения первых i-1 компонент, называется методом Зейделя. Если приведение системы к итерационному виду сделано как это описано в предыдущем параграфе, то расчетная формула для элементов решения
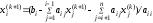 ,
i=1,2,…,
n.
,
i=1,2,…,
n.
В развернутом виде метод Зейделя определяется системой равенств:
x1(k+1) = (b1-a12x2(k)-a13x3(k)-…-a1nxn(k))/a11,
x2(k+1 )= (b2-a21x1(k+1)-a23x3(k)-…-a2nxn(k))/a22,
……………………………………………
xn(k+1) = (bn-an1x1(k+1)-an2x2(k+1)-…-an,n-1xn-1(k+21))/ann.
В сравнении с МПИ метод Зейделя сходится быстрее. Кроме того, при его реализации на компьютере не нужен отдельный массив для хранения нового приближения. Вычисленные компоненты нового вектора x(k+1) заносятся на место соответствующих компонент старого вектора x(k), в этой связи метод Зейделя называют методом последовательных смещений. В МПИ нужно целиком сохранять массив значений x(k), подставляемый в правую часть расчетной формулы (13), до тех пор, пока не сформирован полностью новый массив x(k+1) – результат текущего итерационного шага. Поэтому МПИ называют методом одновременных смещений.
Достаточные условия метода Зейделя такие же как и для МПИ.
Процесс итераций продолжаем до тех пор, пока значения xi(k+1) (i=1,2,…,n) не станут близким к значениям xi(k) с заданной погрешностью .
37. Приведение метода Зейделя к методу простой итерации.
Дана СЛАУ:

Матричная форма:
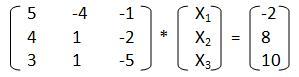
Смотрим на первый этап итерационных методов – он предполагает преобразование исходной системы, а именно матрицы А и вектора b к итерационной форме, где С и d – итерационные формы исходных данных.
Переход к итерационному виду осуществляется по следующим формулам:
cij = -aij/aii di= bi/aii , где i, j = 1,2,3…
Также следует отметить, что, несмотря на эти формулы, диагональные элементы новой матрицы обнуляются, хотя должны быть равны -1.
В итоге для нашей системы должно получиться:
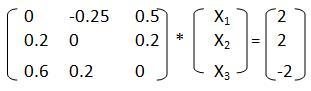
Это "НО" заключается в следующем. Если мы будем преобразовывать исходную систему к итерационной форме, то она не удовлетворит условию сходимости:
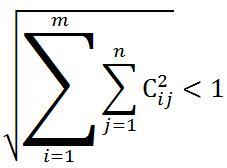 Некоторые
элементы матрицы C будут больше единицы.
А глядя на условие сходимости, становится
понятно, что, если хотя бы один будет
больше единицы, то условие не выполнится,
и решение системы путем простых итераций
не будет найдено.
Некоторые
элементы матрицы C будут больше единицы.
А глядя на условие сходимости, становится
понятно, что, если хотя бы один будет
больше единицы, то условие не выполнится,
и решение системы путем простых итераций
не будет найдено.Поэтому открываем учебник по линейной алгебре и вспоминаем элементарные матричные преобразования! Прежде чем следовать этапам итерационных методов, нужно привести исходную систему к виду, в котором все диагональные элементы были бы максимальными по модулю в своих строках. Только при таком виде матрицы коэффициентов можно надеется на выполнение условия сходимости.
Смотрим нашу начальную систему. Видим, что третий элемент третьей строки по модулю больше других. Оставим его неизменным. Меняем местами первую и вторую строки. Теперь умножаем строку, ставшую первой, на -1 и складываем с новой второй. В итоге получаем:
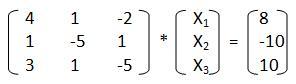
Теперь при подстановке в формулы мы получим итерационную форму верно. К сожалению, это преобразование начальной системы к "благоприятному" виду - чистая аналитика, поэтому записать его в программный код очень сложно, а если даже и попытаться, то в некоторых случаях вероятно возникновение ошибок.
Переходим ко второму этапу: "Проверка условия сходимости" (формулу смотрите выше). Если система не проходит проверку, то приближения не будут сходиться к реальному решению, и ответ получен не будет. В этом случае можно попытаться получить другую "благоприятную" форму. Если условие сходимости выполнено, то стратегия метода простых итераций применима и осуществляется переход к третьему этапу.
В конечном счете, мы получили систему линейных алгебраических уравнений в итерационной форме:
где x1, x2, x3 – приближения, получаемые на текущей итерации за счет приближений полученных на предыдущей итерации - x01, x02, x03.
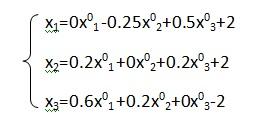
Итерационный процесс в методе простых итераций идет до тех пор, пока вектор приближений не достигнет заданной точности, т.е. пока не выполнится условие выхода:
Max|xi-x0i|<ε, где ε – требуемая точность.
38. Метод последовательной внешней (верхней) релаксации
Рассмотрим одно обобщение метода Зейделя, позволяющее иногда в несколько раз ускорить сходимость итерационной последовательности. Пусть zi(k) – обозначение i-й компоненты k-го приближения к решению системы (1) по методу Зейделя, а обозначение xi(k) будем использовать для i-й компоненты k-го приближения новым методом. Этот метод определим равенством
xi(k+1)=xi(k)+ω(zi(k+1)- xi(k)), (17)
где i=1,2,…,n; k=0,1,2,…; xi(0) – задаваемые начальные значения; ω – числовой параметр, называемый параметром релаксации. Очевидно, при ω=1 метод (3), называемый методом релаксации (ослабления) совпадает с методом Зейделя.
Пользуясь ведёнными здесь обозначениями, запишем на основе метода Зейделя дополнительное к (17) равенство для выражения компонент векторов z(k)=(zi(k))ni=1 через компоненты векторов x(k)= (xi(k))ni=1:
 ,
i=1,2,…,
n.
(18)
,
i=1,2,…,
n.
(18)Таким образом, метод релаксации можно понимать как поочерёдное применение формул (3) и (4) при каждом k=0,1,2,…. Действительно, задав начальные значения x1(0), x2(0),…,xn(0) и параметр ω, при k=0, полагая i=1,2,…,n, вычислим z1(1),x1(1); z2(1),x2(1); …; zn(1),xn(1). Далее вычисляем при k=1, также полагая i=1,2,…,n: z1(2),x1(2); z2(2),x2(2); …; zn(2),xn(2), т.д.
Теорема о сходимости метода релаксации (теорема Островского-Рейча).
Для нормальной системы Ax=b метод релаксации, определяемый формулами (17), (18), сходится при любом х(0) и любом ωε(0;2).
Система Ax=b называется нормальной, если матрица А – симметричная (A=A) и положительно определённая ((Ax,x)>0 для любого x0). Поскольку итерационный процесс (17), (18) содержит параметр, естественно распорядится им так, чтобы сходимость последовательности (х(k)) была наиболее быстрой. Исследование показывает, что оптимальное значение параметра релаксации лежит в интервале ωε(1;2). При этом метод (17),(18) называют методом последовательной верхней релаксации (ПВР). Ввиду неэффективности метода при ωε(0;1), называемого в этом случае методом нижней релаксации, название метод ПВР в последнее время относят ко всему семейству методов (17),(18), т.е. для любых ωε(0;2). При этом случай ωε(1;2) называют сверхрелаксацией.
39.Постановка задачи интерполирования.
Точки совпадений-узлы интерполяций.(Xo,X1,Xn) Условия интерполяции
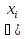 )=f
)=f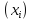 ,
i=0,1…n(бесконечное
множество решений, узлы совпадают)
,
i=0,1…n(бесконечное
множество решений, узлы совпадают)
Класс интерполяционной функции должен быть сужен.
Класс
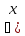 ):ɸ,
f(x)єF
):ɸ,
f(x)єFЧтоб сузить:
1.Вводим базисные функции-
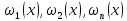
2. Составляем линейную сумму-
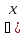 )==
)==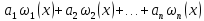 (ее ищем)
(ее ищем)3.Ищем
 и тд, спользуя уловие интерполяции.
и тд, спользуя уловие интерполяции.Подставим в У.И.:


…………………………………………………..
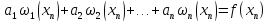
Система совместна(неоднородная). правые не все нулевые. det ненулевой.
4.Составим определитель :
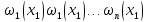
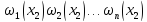
…………………………

Узлы должны быть разными.
Свойствабазисных функций:
1.Система бызисных функций является системой Чебышева.
2.Условие на класс фи: условие полноты(в это классе нет дырок). Это означает, что для любой f(x) найдутся такие коэффициенты
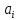 и такое «n», что для любогоƐ>0,
вып. условие |f(x)-
и такое «n», что для любогоƐ>0,
вып. условие |f(x)-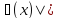 <
Ɛ для сущ. иксов, принадлежащих промежутку.
<
Ɛ для сущ. иксов, принадлежащих промежутку.40.Алгебраическое интерполирование
Начнем с рассмотрения задачи интерполяции в наиболее простом и хорошо исследованном случае интерполирования алгебраическими многочленами. Для заданной таблицы (1) многочлен Pn(x)=a0+a1x+a2x2+… +anxn степени n называется интерполяционным многочленом, если он удовлетворяет условиям (2):
Pn(xi)=yi, i= 0, 1, …, n. (7)
Равенства (7) можно записать в виде системы уравнений:
a0+a1x0+a2x02+… +anx0n= y0,
a0+a1x1+a2x12+… +anx1n= y1, (8)
……………………………………………….
a0+a1xn+a2xn2+… +anxnn= yn
относительно коэффициентов многочлена. Эта система однозначно разрешима, так как система функций 1, x, x2,…,xn линейно независима. Однозначная разрешимость системы следует и из того хорошо известного факта, что определитель этой системы - определитель Вандермонда:
1 x0 x02 … x0n
1 x1 x12 … x1n
Dn(x0, x1,…, xn) = ………….…
1 xn xn2 … xnn
отличен от нуля, если узлы интерполяции попарно различны. Таким образом, существует единственный интерполяционный многочлен степени n, удовлетворяющий условиям (7). В курсе математического анализа доказывается теорема Вейерштрасса: если функция f непрерывна на конечном замкнутом отрезке [a,b], то для всякого >0 существует многочлен Pm некоторой степени m, для которого при любых x[a,b] выполняется неравенство f(x)-Pm(x).
Иначе говоря, для любого конечного замкнутого отрезка семейство алгебраических многочленов является полным в классе непрерывных на этом отрезке функций. Этот факт позволяет ожидать, что при надлежащем выборе узлов и их числа n непрерывную на [a,b] функцию можно на этом отрезке интерполировать сколь угодно точно алгебраическим многочленом.
На практике система (8) редко используется для вычисления коэффициентов интерполяционного многочлена ak, так как в большинстве приложений они просто не нужны. Кроме того, при n>4 система (8) становится плохо обусловленной. Существуют различные удобные явные формы записи интерполяционного многочлена, которые и применяются на практике.
41.Интерполяционный полином в форме Лагранжа.
Ln(xi) = l0(x)*f(x0) + l1(x)*f(x1) +…+ ln(x)*f(xn). l0(x0) = 1; l0(x1) = 0
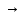 li(
li(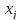 )
=
)
=
li(x) = C*(x-x0)(x-x1)*…*(x-
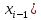 (x-
(x-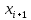 )*…*(x-xn);
где С=const
- находится из условия x
= xi.
)*…*(x-xn);
где С=const
- находится из условия x
= xi.li(xi) = 1; li(xi) = C(xi – x0)……(xi – xn) = 1; C =
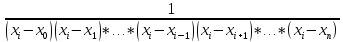
li(x) =
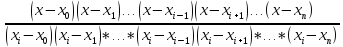 =
=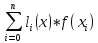 - развернутая форма полинома Лагранжа.
- развернутая форма полинома Лагранжа.
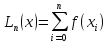 .
.42.Свернутая форма полинома Лагранжа.
Введем в рассмотрение полином w(x)=(x-x0) (x-x1)…(x-xn) полином (n+1) –ой степени. Числитель в i: w(x)/(x-xi)
w’(x) = (x-x1)…(x-xn)+(x-x0)(x-x2)…(x-xn)+…(x-xi+1)(x-xi-1)…(x-x0) +(x-x0)…(x-xn-1).
Ln(x)=
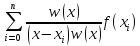
43. Погрешность алгебраического интерполирования.
Оценку погрешности интерполяции функции f(x) дифференцируемой n+1 раз на отрезке [a,b], содержащем узлы интерполяции xi (i= 0,1, n) удобно выполнить, используя выражение:
R n(x)=f(x)-Pn(x)[M n+1/n+1!]n+1(x) (12)
как следствие из теореме о погрешности
Обратим внимание на одну из интерполяционных задач, связанных с построенными представлениями Rn. Пусть нужно выполнить интерполирование функции во всех точках отрезка [a,b]. Погрешность его зависит от выбора узлов xi, точки х и свойств функции f. Если интерполируется одна определенная функция f, то точность интерполирования характеризуется величиной maxRn(x). Когда мы интерполируем не одну функцию f, а некоторое множество функций f, то точность может быть оценена величиной sup maxRn(x)=m=m (x0, x1, …, xn). (13)
Эта величина зависит только от выбора узлов хi (i=0,1, …, n).
Поставим задачу о выборе узлов xi, которые можно было бы считать наилучшими при интерполировании всех функций f на [a,b] из взятого множества. Такими узлами естественно считать те, для которых величина m(x0, x1,…,x n) достигает наименьшего значения. Найдем такие узлы для множества всех функций с непрерывной производной порядка n+1 на [а,b]. Изменим на время эту задачу и рассмотрим функции f, для которых при некотором произвольно взятом положительном M выполняется неравенство
f(n+1)(x) M. (14)
Для таких функций погрешность Rn(x) может быть оценена следующим неравенством, которое сразу вытекает из (11):
maxRn(x) [M/(n+1!)]max(x).
Эта оценка является не улучшаемой, так как в ней имеет место знак равенства, когда f есть следующий многочлен степени n+1:
f=[M/(n+1)!](x n+1+c1xn+…)
и, следовательно,
sup maxRn(x)=[M/(n+1)!]max(x). (15)
Первый множитель правой части (15) не зависит от выбора узлов хi, и поэтому наилучшими узлами при интерполировании функций f, удовлетворяющих условию (14), нужно признать те хi, для которых
max(x)=min. (16)
Это заключение верно при всяких М в неравенстве (14). Можно поэтому утверждать, что такие узлы будут наилучшими при интерполировании всяких функций f с непрерывной производной порядка n+1 на [а,b].
44.Интерполирование сплайнами
Интерполяционные формулы Лагранжа, Ньютона и Стирлинга и др. при использовании большого числа узлов интерполяции на всем отрезке [a, b] часто приводят к плохому приближению из-за накопления погрешностей в процессе вычислений [2]. Кроме того, из-за расходимости процесса интерполяции увеличение числа узлов не обязательно приводит к повышению точности. Для снижения погрешностей весь отрезок [a, b] разбивается на частичные отрезки и на каждом из них функцию f(x) заменяют приближенно полиномом невысокой степени. Это называется кусочно-полиномиальной интерполяцией.
Один из способов интерполирования на всем отрезке [a, b] является интерполирование сплайнами.
Сплайном называется кусочно-полиномиальная функция, определенная на отрезке [a, b] и имеющая на этом отрезке некоторое количество непрерывных производных. Преимущества интерполяции сплайнами по сравнению с обычными методами интерполяции – в сходимости и устойчивости вычислительного процесса.
На практике предпочитают для получения сходящегося интерполяционного процесса использовать кусочно-полиноминальную интерполяцию. Для этого отрезок [а,b] разделяют на части точками и интерполируют не при помощи одного многочлена на всем отрезке [а,b] а для каждого частичного отрезка избирают свои узлы и строят свой интерполирующий многочлен невысокой степени. Однако этот способ приближения имеет недостаток: в точках «стыка» двух соседних многочленов производная, как правило, имеет разрыв. Часто это обстоятельство не играет большой роли. Вместе с тем нередко требуется, чтобы аппроксимирующая функция была гладкой и тогда простейшая кусочно-гладкая интерполяция становиться неприемлемой. Естественна потребность в наличии аппроксимирующих функций, которые сочетали бы в себе локальную простоту многочлена невысокой степени и глобальную на всем отрезке [а,b] гладкость, привела к появлению так называемых гладких сплайн-функций или сплайнов – специальным образом построенных гладких кусочно-многочленных функций.
Дадим строгое определение сплайна. Пусть отрезок [а,b] разбит точками a=x0x1xn=b на n частичных отрезков [xi-1,xi]. Сплайном Sm(x) степени m называется определенная на [a,b] функция, принадлежащая классу Cp[a,b] p
раз непрерывно дифференцируемых функций, такая, что на каждом частичном промежутке [xi-1,xi] i=1,…, n – это многочлен m-ой степени.
Разность d=m-p между степенью сплайна и наивысшим порядком непрерывной на отрезке [а,b] производной называется дефектом сплайна.
Пусть функция y=f(x) задана таблицей своих значений (1). Сплайн Sm(x) называется интерполяционным, если Sm(xi)= y(xi) для всех i= 0, 1,…, n. Значение si= Sm(xi) называется наклоном сплайна в точке xi.
Простейший пример сплайна дает непрерывная кусочно-линейная функция, являющаяся сплайном первой степени (линейным сплайном) с дефектом, равным единице. Действительно на отрезке [а,b] сама функция (нулевая производная) непрерывна. В то же время на каждом частичном отрезке S1(x) совпадает с некоторым многочленом первой степени.
Наиболее широкое распространение на практике получили сплайны S3(x) третьей степени (кубические сплайны) с дефектом, равным 1 или 2. Такие сплайны на каждом из частичных отрезков [xi-1,xi] совпадают с кубическим многочленом. Дадим определение кубического сплайна.
Кубическим сплайном дефекта 1, интерполирующим на отрезке [а,b] данную функцию f(x), называется функция
g(x)={gi(x)=ai+bi(x-xi-1)+ci(x-xi-1)2+d i(x-xi-1)3 при x[xi-1,xi] и i=1, …, n},
удовлетворяющая следующим условиям:
условиям интерполяции - g(xi)=fi, i=0, …, n;
двойной непрерывной дифференцируемостью - g(x)C2[a,b];
краевым условиям.
Краевые условия могут быть весьма разнообразными. Можно задавать в граничных точках конкретные наклоны графика сплайна:
g(x0) = f (a), g(xn) = f (b)
или конкретную кривизну:
g(x0) = f (a), g(xn) = f (b).
Часто задают условия “свободного провисания”:
g(x0) = 0, g(xn) = 0.
Эти условия определяют так называемый естественный кубический сплайн (или чертежный сплайн).
Рассмотрим построение естественного кубического сплайна. Для этого надо найти 4n его коэффициентов { ai, bi, ci, di; i=1,…, n}. Для нахождения этих коэффициентов имеем следующие соотношения:
из условий интерполяции g1(x0)=f0, gi(xi)=fi, i=1,2,…, n; (уравнений (n+1))
