§29. Обращение преобразования Лапласа.

Решение ДУ операционным методом сводится к задаче отыскания оригинала по изображению. Ответ на этот вопрос дает

Теорема Меллина. Пусть f(t)- оригинал, а F(p) его изображение при Re p>a, тогда в точках непрерывности f(t) справедлива формула Меллина

для  x>a.

Замечание. Несобственный интеграл вычисляется вдоль прямой Rep=x>a и понимается в смысле главного значения: .

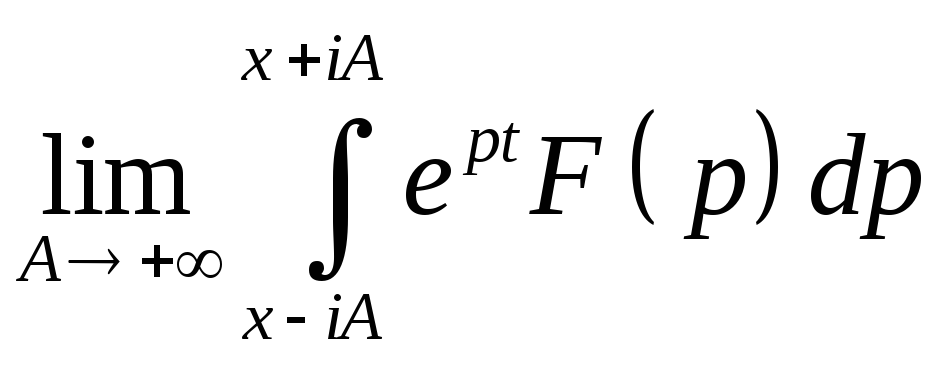Доказательство.

Рассмотрим вспомогательную функцию , x>a. Эта функция кусочно-непрерывна и экспоненциально убывает на бесконечности. Такие функции могут быть представлены при помощи интеграла Фурье

Выражая , получим

Здесь учтено, что f(t)=0 при t<0. Обозначим p=x+i и получим преобразование Лапласа от f(t) во внутреннем интеграле.

.

Интеграл берется в комплексной плоскости по прямой, параллельной мнимой оси, лежащей правее прямой Rep=a.

Значение интеграла, очевидно, не зависит от выбора x>a.

Замечание. При доказательстве мы перешли к преобразованию Фурье от оригинала. Поэтому формула Меллина определяет значение оригинала по изображению только в точках непрерывности. В точках разрыва первого рода интеграл Меллина сходится к полусумме предельных значений оригинала

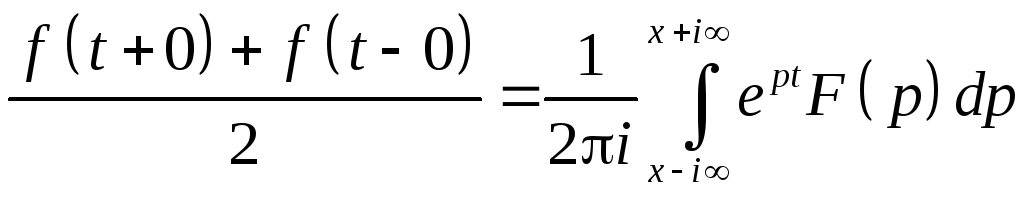
Если же заранее не известно, является ли функция F(p) изображением какого-либо оригинала, то для обращения преобразования Лапласа полезно установить хотя бы некоторые достаточные условия существования оригинала.

Для доказательства нам понадобиться лемма Жордана в правой и левой полуплоскости.

1. Если f(z) удовлетворяет условиям Леммы Жордана при Rez>0, то при >0 , C"_R - полуокружность |z|=R Rez>0.

2. Если f(z) удовлетворяет условиям Леммы Жордана при Rez<0, то при >0 , C'"_R - полуокружность |z|=R Rez<0.

Теорема 29.2. Пусть F(p) C^(Re p>a) и 1) |F(p)|=>0 при |p| , Re p>a равномерно относительно аргумента.  Re p=x>a: 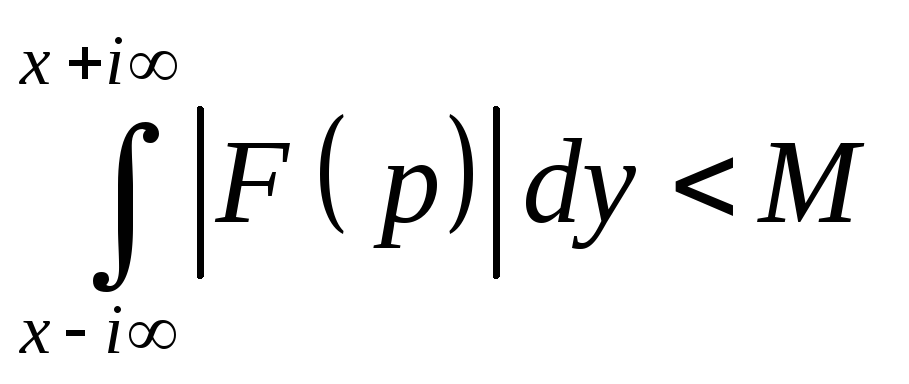(равномерно ограничен по x). Тогда  f(t)A(a): f(t)F(p) и оригинал вычисляется по формуле Меллина

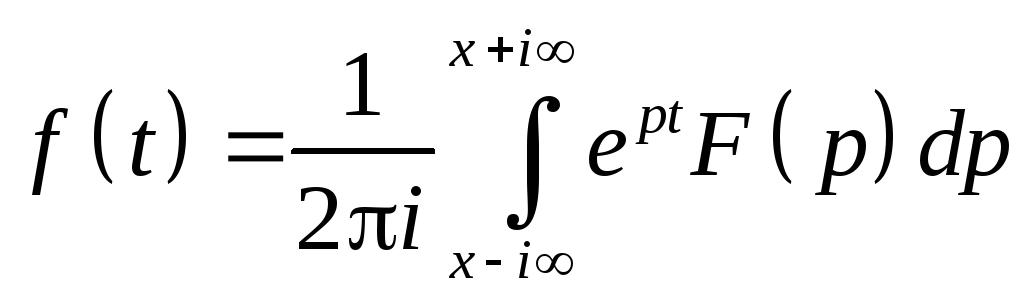для  x>a.

Доказательство. Надо доказать, что интеграл несобственный 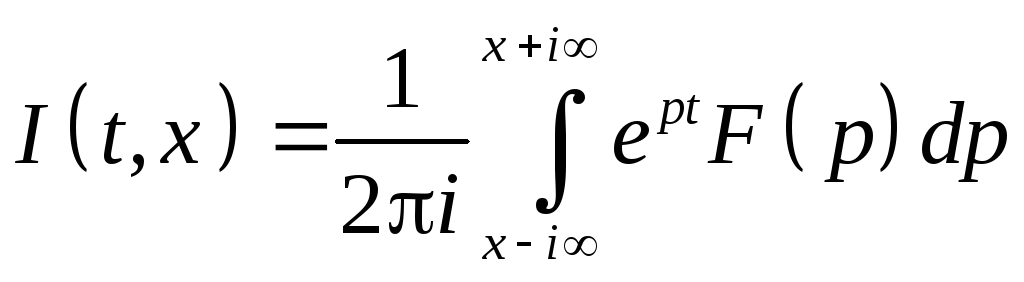является оригиналом F(p). Первым делом возникает вопрос о его существовании.

Существование I(t,x) для  x>a;

Эта оценка, в частности, показывает, что I(t,x) имеет ограниченную степень роста a.

Замечание: на[0,T] (конечный интервал по времени) интеграл сходится равномерно по t.

Далее следует установить, что

1. Интеграл I(t,x)не зависит от выбора x и определяет функцию f(t) лишь одной переменной t, причем эта функция обладает конечной степенью роста.

2. При t<0 f(t)=0

3. Изображение f(t) – это исходная функция F(p).

Докажем каждое из высказанных утверждений.

1. Рассмотрим в область Re p>a замкнутый контур 

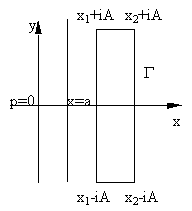
Т.к. F(p)C^(Re p>a), то по теореме Коши ; Устремим А к , тогда по условию теоремы |F(p)|=>0 при |p|, Re p>a интегралы по горизонтальным отрезкам дадут в пределе 0. Действительно, интеграл по отрезку конечной длины от произведения ограниченной и убывающей к нулю функций.

Интегралы же по вертикальным прямым перейдут в несобственные интегралы .

Тем самым интеграл не зависит от выбора x.

2. Докажем, что I(x,t)0, t<0.

Исследуем I(x,t) при t<0. Рассмотрим замкнутый контур 

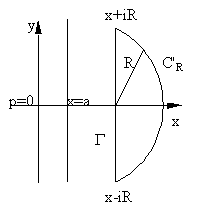
По теореме Коши . В силу замечания к Лемме Жордана при R интеграл по дуге С'_R при t<0. Поэтому при t<0. Re p>a и  x>a.

3. Покажем, что f(t)F(p). Рассмотрим изображение при некотором произвольном p₀.

Т.к. внутренний интеграл не зависит от x, то выберем x: a<x<p₀. Изменим порядок интегрирования, что возможно в силу равномерной сходимости соответствующих интегралов.

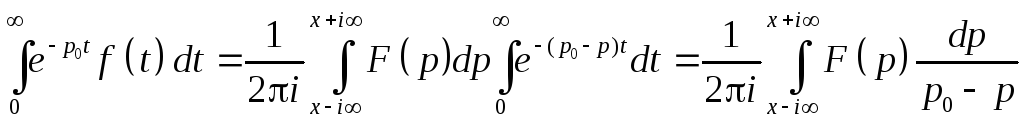
Этот интеграл можно вычислить с помощью вычетов, т.к. при подынтегральная функция убывает быстрее, чем . Замыкая контур в правой полуплоскости, учитывая, что контур обходится по часовой стрелке, получим

=-Выч[F(q)/(p- p₀),p₀]=F(p₀)

Здесь учтено, что p₀ – полюс первого порядка подынтегральной функции 

Для вычисления оригинала по изображению при помощи формулы Меллина может быть полезна следующая теорема.

Теорема разложения I. Если F(p) C^(p>R) и существует разложение , то оригинал .

Доказательство.

- степенной ряд, сходящийся равномерно везде внутри своей области сходимости. Равномерно сходящийся ряд можно почленно проинтегрировать.

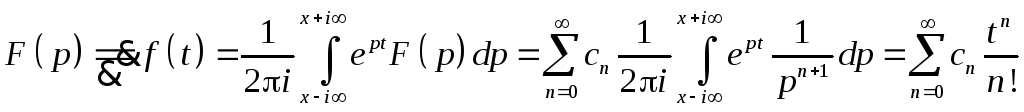
Пример.

1.

Ряд справа представляет собой разложение весьма важной специальной функции - функции Бесселя нулевого порядка.

2.

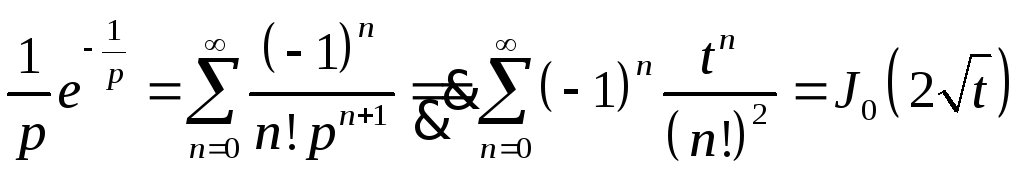
Теорема разложения II. Если  аналитическое продолжение F(p) в левую полуплоскость, имеющее конечное число N изолированных особых точек p_n и удовлетворяющее условиям Леммы Жордана, то

.

Доказательство.

Для вычисления интеграла 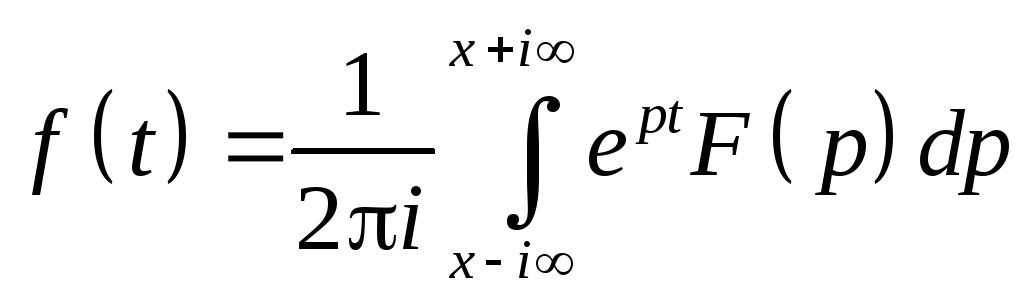применим теорию вычетов. Замкнем прямолинейный отрезок интегрирования полуокружностью в левой полуплоскости. Интеграл по замкнутому контуру равен на сумму вычетов в изолированных особых точках внутри этого контура. Интеграл по этой полуокружности в силу замечания к Лемме Жордана при увеличении радиуса стремится к нулю  .

§30. Решение задачи Коши для линейного обыкновенного дифференциального уравнения с постоянными коэффициентами операционным методом.

Задача Коши для дифференциального уравнения это ДУ с дополнительными условиями, заданными в одной точке. Если дополнительные условия заданы при t=0 их естественно назвать начальными. Общий вид такой задачи следующий

a₀y⁽ⁿ⁾(t)+ a₁y^(n-1)(t)...+a_ny(t)=f(t);

y(0)=y_o, y’(0)=y₁, ... y^(n-1)(0)=y_n

Если правая часть ДУ равно 0, то уравнение называется однородным, и неоднородным в противном случае. Если же все правые части в начальных условиях y_o=y₁=... =y_n=0, то граничные условия называются однородными и неоднородными в противном случае.

В силу линейности задачи решение задачи Коши для линейного обыкновенного дифференциального уравнения может быть найдено как сумма двух решений: решения задачи Коши для однородного уравнения с неоднородными начальными условиями и решения задачи Коши для неоднородного уравнения с однородными начальными условиями. Действительно, если

a₀z⁽ⁿ⁾(t)+ a₁z^(n-1)(t)...+a_nz(t)=0;

z(0)=y_o, z’(0)=y₁, ... z^(n-1)(0)=y_n

a₀x⁽ⁿ⁾(t)+ a₁x^(n-1)(t)...+a_nx(t)=f(t);

x(0)=0, x’(0)=0, ... x^(n-1)(0)=0

тогда y(t)=z(t)+x(t) является решением исходной задачи.

Поэтому есть смысл рассмотреть отдельно две эти задачи.

1. Однородное уравнение с неоднородными начальными условиями.

a₀y⁽ⁿ⁾(t)+ a₁y^(n-1)(t)...+a_ny(t)=0;

y(0)=y_o, y’(0)=y₁, ... y^(n-1)(0)=y_n

Пусть y(t) Y(p), тогда для изображения неизвестной функции Y(p) получим алгебраическое уравнение, которое элементарно разрешается

a₀ p ⁿ Y(p)-y₀/p-y₁/p ² -…-y_n/p ⁿ+ a₁p^n-1 Y(p)-y₀/p-y₁/p ² -…-y_n-1/p ^n-1+...+a_n Y(p)=0

Y(p)=Q_n-1(p)/P_n(p).

где Q_n-1(p) и P_n(p) – полиномы.

Обращая преобразование Лапласа найдем искомое решение задачи.

2. Неоднородное линейное ДУ с однородными начальными условиями.

a₀y⁽ⁿ⁾(t)+ a₁y^(n-1)(t)...+a_ny(t)=f(t), t>0;

y(0)=...=y^(n-1)(0)=0;

Пусть f(t)F(p); y(t) Y(p), тогда для изображения неизвестной функции Y(p) получим алгебраическое уравнение, которое элементарно разрешается

a₀ p ⁿ Y(p)+ a₁p^n-1 Y(p)...+a_n Y(p)=P_n(p)Y(p)=F(p)

Y(p)=F(p)/P_n(p).

Можно “в лоб” искать оригинал от этого изображения и он будет решение исходной задачи, но можно немного упростить задачу, воспользовавшись интегралом Дюамеля. При этом не придется даже искать изображения функции, стоящей в правой части уравнения.

Пусть сначала было найдено решение x(t) более простой задачи: тоже самое уравнение, с тем же однородными начальными условиями, но с единичной функцией в правой части (единичное воздействие на систему)

a₀x⁽ⁿ⁾(t)+ a₁x^(n-1)(t)...+a_nx(t)=1, t>0;

x(0)=...=x^(n-1)(0)=0;

Пусть x(t) X(p), тогда

a₀ p ⁿ X(p)+ a₁p^n-1 X(p)...+a_n X(p)=P_n(p)X(p)=1/p

X(p)=1/pP_n(p).

Итак, y(t) Y(p)=pX(p)F(p) .

Т.о. используя интеграл Дюамеля, мы получили решение для неоднородного уравнения в однородными начальными условиями в виде свертки решения более простой задачи с единичным воздействием на систему и правой части исходного уравнения.

Примеры.

1. Рассмотрим задачу Коши для однородного ДУ.

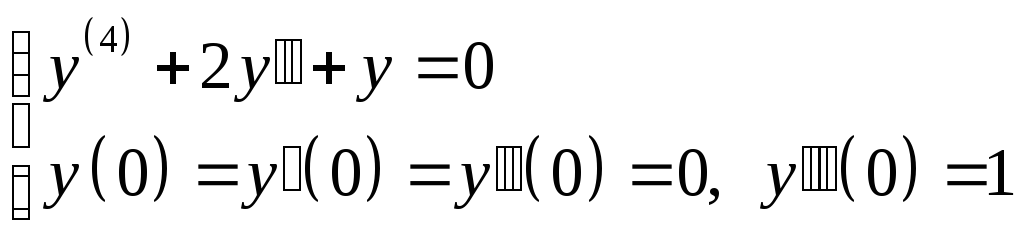
Применим преобразование Лапласа , , , , . Для изображений уравнение превращается в алгебраическое

Откуда

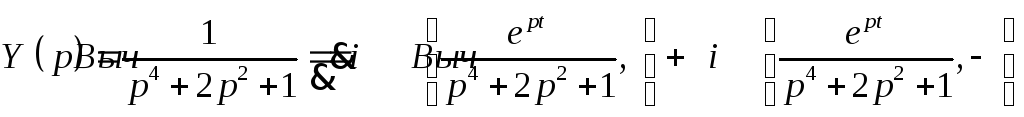
Обе особые точки – полюса второго порядка.

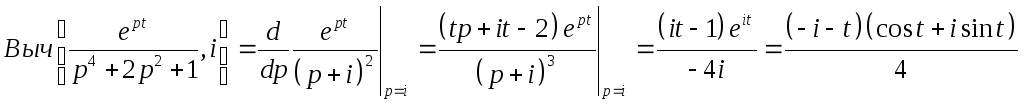
Тогда искомая функция .

2. Рассмотрим задачу Коши для неоднородного ДУ

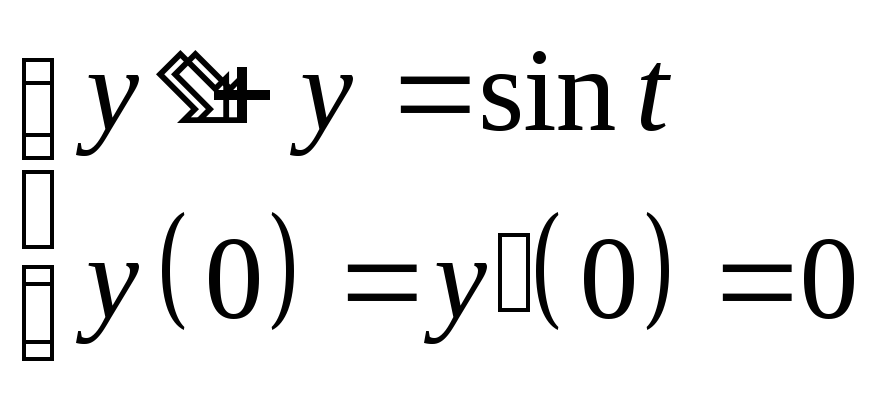
Применим преобразование Лапласа , , . Для изображений уравнение превращается в алгебраическое

Откуда

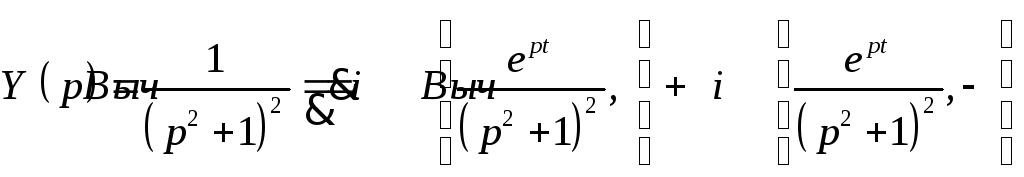
И снова искомая функция .