
Лекции / семестр4 / Лекции МП-2 (Альшина) / Pr14
.doc§27. Основные понятия операционного исчисления.
Операционное исчисление - это аппарат интегральных преобразований, позволяющий заменить операции дифференцирования и интегрирования функции действительной переменной (известной или неизвестной, заданной или искомой) на алгебраические операции с параметрами интегральных преобразований.
Понятие преобразования Лапласа.
Класс рассматриваемых функций действительной переменной, называемых оригиналами f(t), определенные при -<t<, обладающие следующими свойствами
1) f(t)0, при t<0
2) f(t)- кусочно-непрерывна при t>0, т.е. для конечного [a,b] f(t) имеет лишь конечное число разрывов I рода.
3) M>0 и a'>0 : |f(t)|<Mea't при t
Определение. Функция, удовлетворяющая условию 3) называется функцией ограниченной степени роста. inf a'=a - показатель степени роста.
Замечание.
Требование кусочной гладкости избыточно
и может быть ослаблено, например, до
локальной интегрируемости и класс
оригиналов тем самым может быть расширен
(например
![]() может быть оригиналом), но для упрощения
доказательств всех теорем будем требовать
кусочной гладкости.
может быть оригиналом), но для упрощения
доказательств всех теорем будем требовать
кусочной гладкости.
Класс А(а)- класс функций ограниченной степени роста.
Примеры 1. f(t)=tn A(0), a=0, т.к. tn<Mea't для a'>0.
-
f(t)=exp(2t2) А(а) для a.
3. f(t)=sint exp(2t) A(2)
Определение.
Преобразованием
Лапласа функции
f(t)
класса А(а)
называется функция комплексной переменной
F(p),
определяемая соотношением
 .
Если
F(p),
то обозначают f(t)
.
Если
F(p),
то обозначают f(t)![]() F(p)
и говорят, что
f(t)-оригинал,
F(p)-изображение.
F(p)
и говорят, что
f(t)-оригинал,
F(p)-изображение.
Для каких p F(p) ?
Теорема 27.1 Если f(t)A(a), то F(p) при Re p>a и в области Re px0>a интеграл сходится равномерно по р.
Доказательство.
Возьмем для x>a; Re p=x>a. Очевидно, |f(t)|<Meat. Оценим

при Re p=x>a F(p).
Существование доказано. Для доказательства равномерной сходимости интеграла по параметру р в области Re px0>a можно воспользоваться достаточным мажорантным признаком Вейерштрасса.
Т.к.
|f(t)|<Meat,
x0>a,
то
![]() всюду в области Re px0>a,
причем мажоранта не зависит от р.
всюду в области Re px0>a,
причем мажоранта не зависит от р.
Каковы свойства F(p) – функции комплексного переменного?
Теорема 27.2. В области Rep>a (f(t)A(a)) F(p) C(Re p>a).
Доказательство. Разобьем область t[0,) на произвольные отрезки конечной длины. Число отрезков бесконечно, длина каждого - конечна!
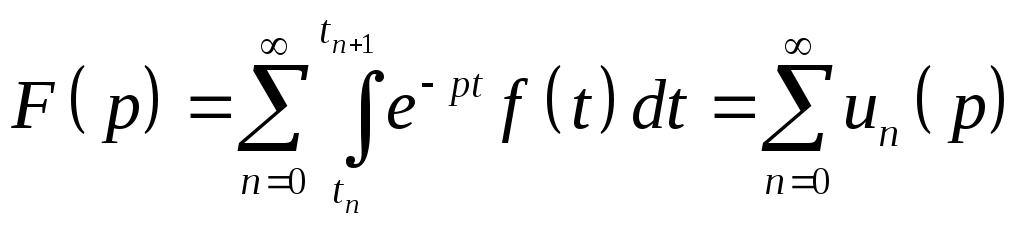
Функциональный
ряд из аналитических функций
![]() (они аналитичны, т.к. производные по
параметру p непрерывны)
равномерно сходится к F(p)
в силу равномерной сходимости интеграла
при Re px0>a.
Такой ряд сходится к аналитической
функции, более того его можно почленно
интегрировать и дифференцировать под
знаком интеграла по параметру p.
В силу произвольности x0
(они аналитичны, т.к. производные по
параметру p непрерывны)
равномерно сходится к F(p)
в силу равномерной сходимости интеграла
при Re px0>a.
Такой ряд сходится к аналитической
функции, более того его можно почленно
интегрировать и дифференцировать под
знаком интеграла по параметру p.
В силу произвольности x0
F(p) C(Re p>a).
Замечание.
Т.к. u(k)n(p)
=>F(k)(p)
при Re px0>a,
то

§28. Свойства изображений.
Найдем изображения ряда элементарных функций про помощи определения.
-
Единичная функция Хевисайда -
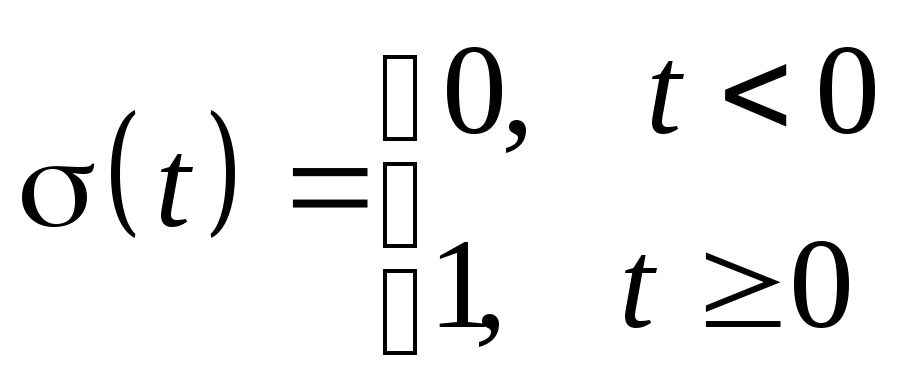
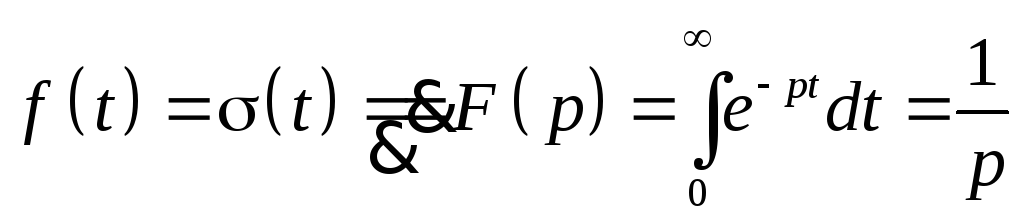 ,
причем (t)А(0)
F(p)C(Re
p>0).
,
причем (t)А(0)
F(p)C(Re
p>0).
Замечание. Всюду в дальнейшем будем под функцией f(t) понимать произведение f(t)(t). Тем самым свойство 1) из определения оригинала будет автоматически выполнено.
-
Показательная функция
f(t)=et при Re p>
Re
;
при Re p>
Re
;
-
Степенная функция
f(t)=t ;
;
Здесь
введено стандартное обозначение
 - гамма-функция,
часто встречающийся в различны областях
математики несобственный интеграл,
зависящий от параметра. Свойства
гамма-функции хорошо изучены, в частности,
для целочисленных значений параметра,
она явно вычисляется
- гамма-функция,
часто встречающийся в различны областях
математики несобственный интеграл,
зависящий от параметра. Свойства
гамма-функции хорошо изучены, в частности,
для целочисленных значений параметра,
она явно вычисляется
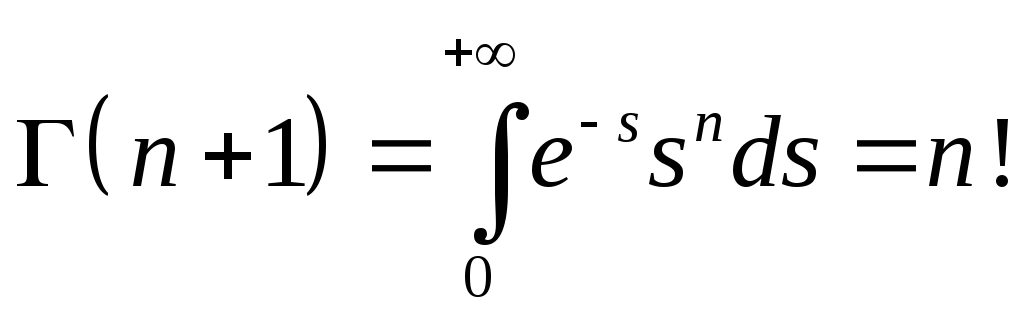 ,
применяя n
раз интегрирование по частям.
,
применяя n
раз интегрирование по частям.
Т.о.
![]()
 ,
а вместе с ней и образ степенной функции,
существует для
,
а вместе с ней и образ степенной функции,
существует для
![]() .
Заметим, что при
.
Заметим, что при
![]() степенная функция не удовлетворяет
свойству 2) в определении оригинала (при
t0
терпит разрыв II
рода). Тем ни менее преобразование
Лапласа для нее существует, и весь
аппарат операционного исчисления для
нее работает. Это говорит лишь о том,
что класс оригиналов может быть расширен.
степенная функция не удовлетворяет
свойству 2) в определении оригинала (при
t0
терпит разрыв II
рода). Тем ни менее преобразование
Лапласа для нее существует, и весь
аппарат операционного исчисления для
нее работает. Это говорит лишь о том,
что класс оригиналов может быть расширен.
tА(0) F(p)C(Re p>0).
Следующие свойства изображения помогут находить преобразования Лапласа от более сложных функция, не прибегая к непосредственному интегрированию.
-
Линейность изображений имеет место в силу линейности интеграла
![]() =F(p)
при Re p>
max ai
=F(p)
при Re p>
max ai
Это свойство позволяет найти изображения тригонометрических функций.
![]() Re p>
|Im
|
Re p>
|Im
|
![]() Re p>
|Im
|
Re p>
|Im
|
a0+a1t+a2t2+…antn![]()
-
Подобие. Пусть
 при Re p>a,
тогда
при Re p>a,
тогда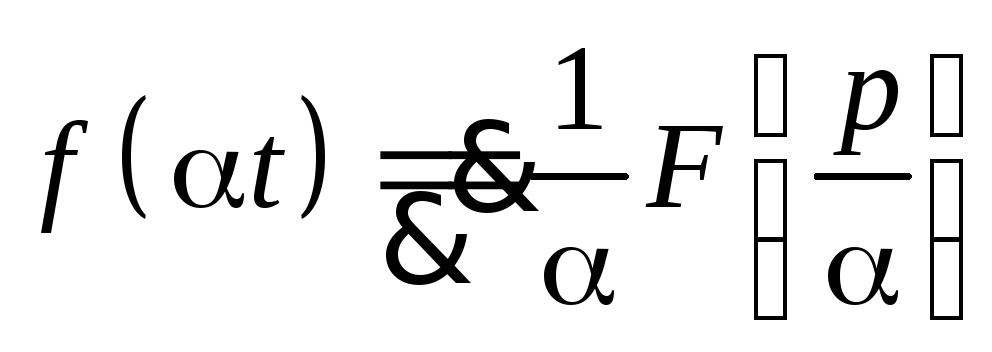 ,
,
Доказательство.
 Re p>a
Re p>a
-
Теорема запаздывания. Пусть
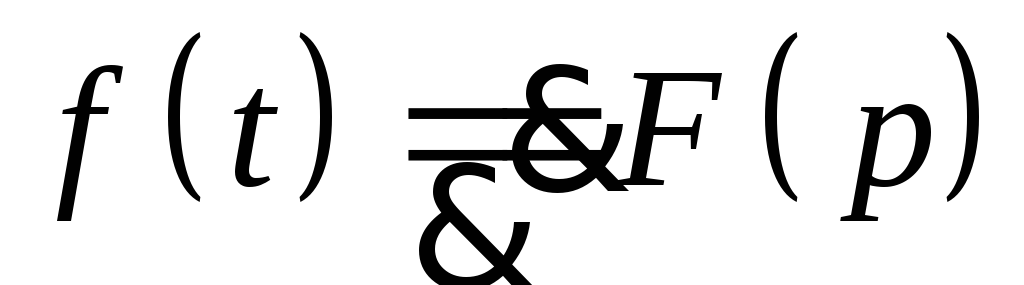 при Re p>a,
тогда запаздывающая функция
при Re p>a,
тогда запаздывающая функция

![]() Доказательство.
Доказательство.
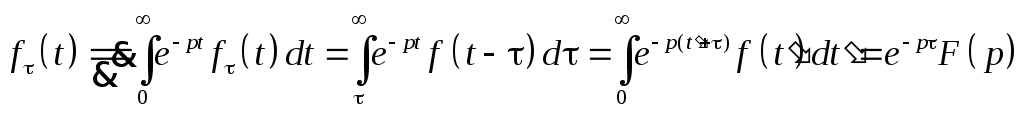 Re p>a
Re p>a
Пример.
1)Изображение
прямоугольного импульса.
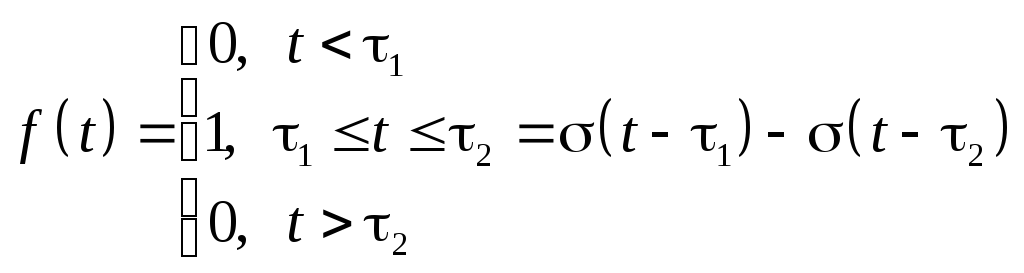
![]()
-
Пилообразный импульс

![]()
-
Ступенчатый импульс
![]() +….
+….
![]()
4.
Теорема смещения.
Пусть
![]() при Re p>a,
тогда помножение оригинала на экспоненту
при Re p>a,
тогда помножение оригинала на экспоненту
![]() соответствует смещению аргумента
изображения
соответствует смещению аргумента
изображения
![]()
Изображение существует при Re(p-)>a
Доказательство.

5.
Изображение производной.
Пусть f(t) и f'(t)
удовлетворяют
условию существования изображения.
Пусть
![]() при Re p>a.
Тогда
при Re p>a.
Тогда
![]() .
.
Доказательство.
![]() .
.
Аналогично,
если
![]() удовлетворяет
условиям существования изображения и
удовлетворяет
условиям существования изображения и
![]() при Re p>a.
Тогда
при Re p>a.
Тогда
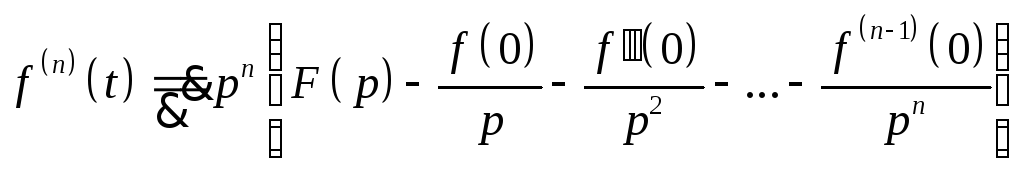 .
.
Формула
особенно упрощается, если
![]() .
Тогда
.
Тогда
![]() .
.
Используя формулы изображения производных любое линейное дифференциальное уравнение с постоянными коэффициентами сводится к алгебраическому уравнению для изображения.
6. Изображение интеграла.
Пусть
![]() при Re p>a.
Тогда
при Re p>a.
Тогда
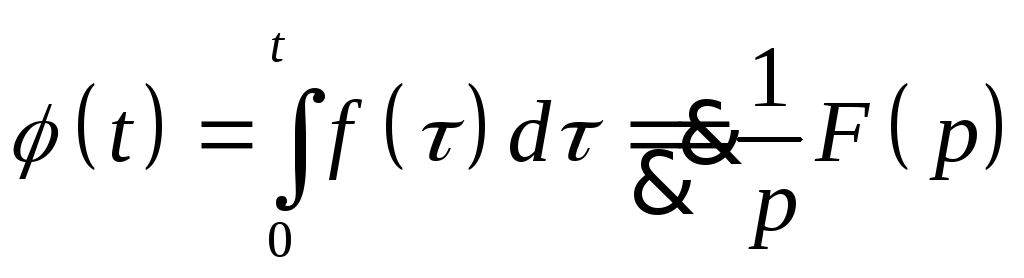 .
.
Доказательство.
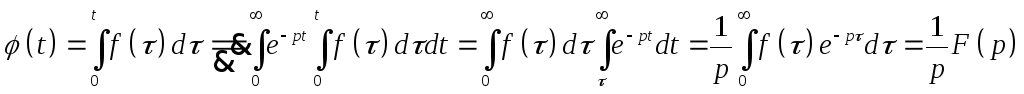 7.
Изображение свертки.
Определение.
Сверткой двух функций f1(t)
и f2(t)
называется
7.
Изображение свертки.
Определение.
Сверткой двух функций f1(t)
и f2(t)
называется

Справедливость последнего равенства легко проверить, сделав замену переменной интегрирования t-=t’.
Пусть
![]() при Re p>a1
и
при Re p>a1
и
![]() при Re p>a2.
Тогда изображение их свертки равно
произведению изображений
при Re p>a2.
Тогда изображение их свертки равно
произведению изображений
 при Re
p>max{a1,a2}.
при Re
p>max{a1,a2}.
(теорема Бореля о свертке)
Доказательство.
Сначала покажем, что свертка двух функций с ограниченными степенями роста так же является функцией с ограниченной степенью роста и может быть оригиналом изображения Лапласа.
Итак,
![]() и
и
![]() ,
тогда их свертка
,
тогда их свертка

Показатель степени роста свертки a=max{a1,a2} очевидно равен максимальной степени роста функций f1(t) и f2(t).
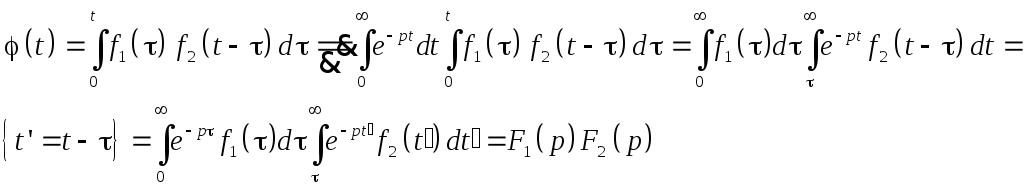
8. Интеграл Дюамеля.
Пусть
![]() при Re p>a1
и
при Re p>a1
и
![]() при Re p>a2.
Тогда при Re p>max{a1,a2}
верно соотношение
при Re p>a2.
Тогда при Re p>max{a1,a2}
верно соотношение
![]()
Доказательство.
![]() .
.
9. Дифференцирование изображения.
Пусть
![]() при Re p>a.
Тогда
при Re p>a.
Тогда
![]() .
.
Доказательство.

9. Интегрирование изображения.
Пусть
![]() при Re p>a.
Тогда
при Re p>a.
Тогда
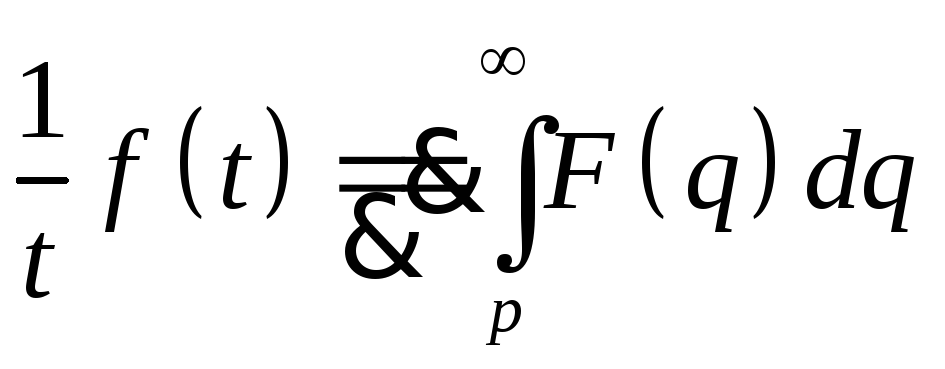 .
.
Доказательство.

Полезно иметь перед глазами следующую таблицу изображений и их свойств. Она поможет и при нахождении изображений и при обращении преобразования Лапласа.
|
Оригинал |
Изображение |
Условия существования |
|
|
|
Re p>0 |
|
|
|
Re p>0 |
|
et
|
|
Re p> Re |
|
|
|
Re p> |Im |
|
|
|
|
Re p> |Im | |
|
|
|
Re p> Re |
|
|
|
Re p> Re |
-
Линейность
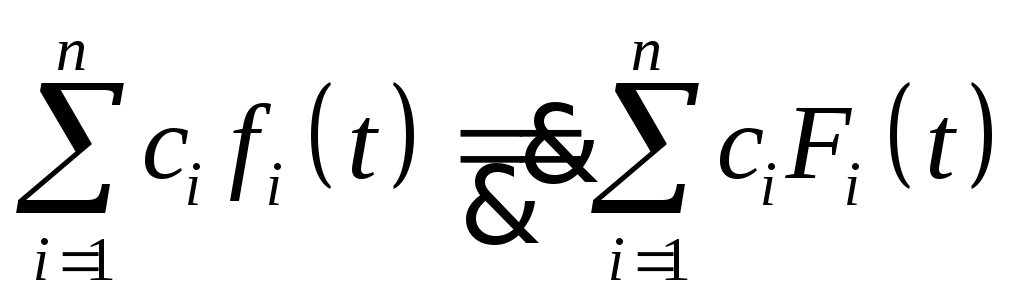
-
Подобие
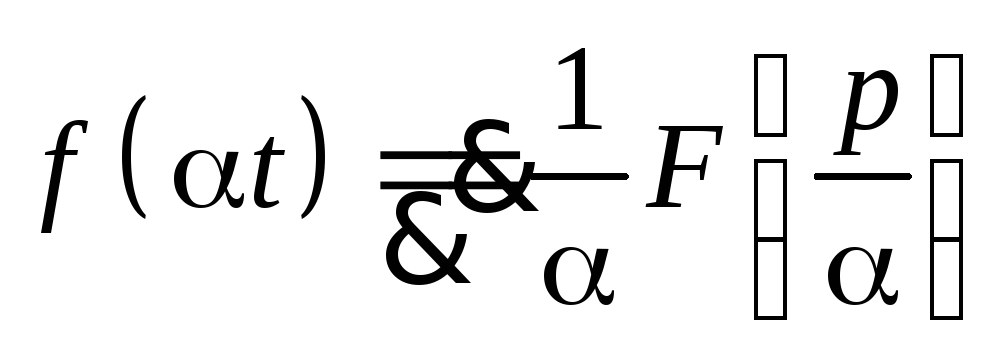 ,
,
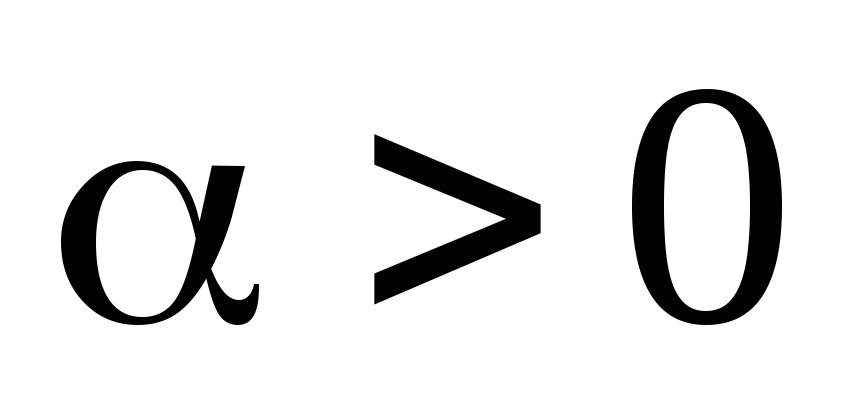
-
Теорема запаздывания
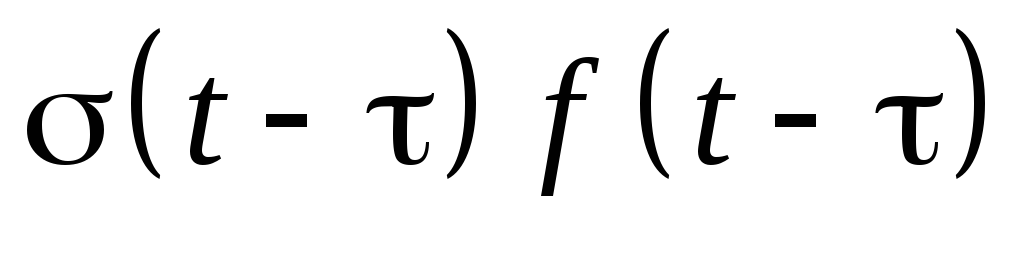

-
Теорема смещения
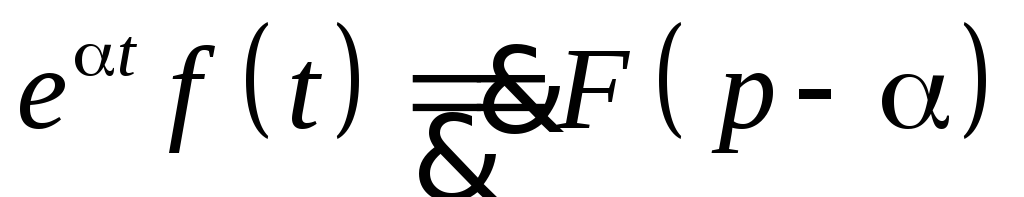
-
Изображение производной

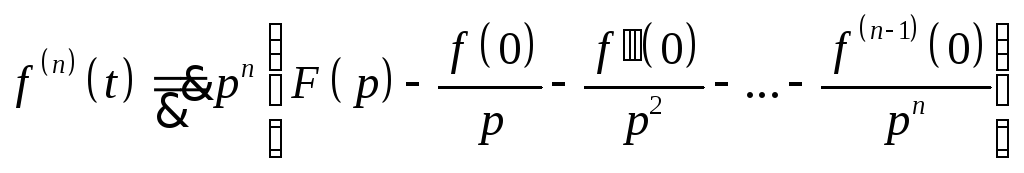
-
Изображение интеграла
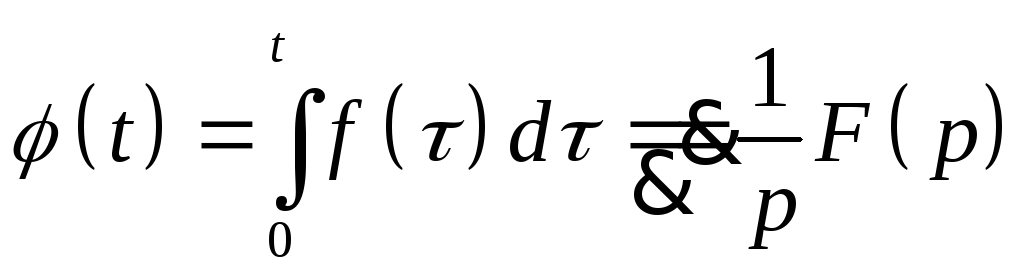
-
Дифференцирование изображения
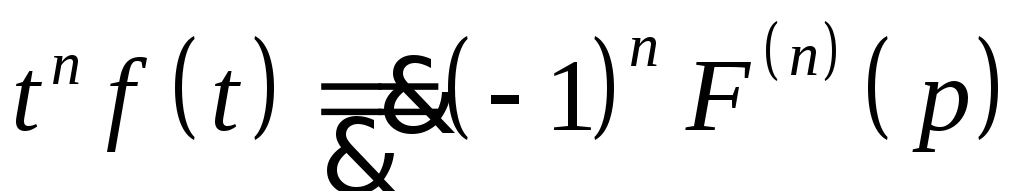
-
Интегрирование изображения
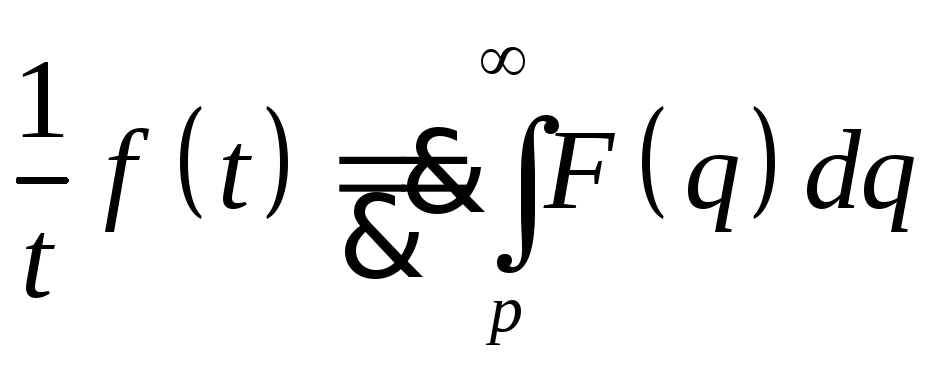
-
Изображение свертки
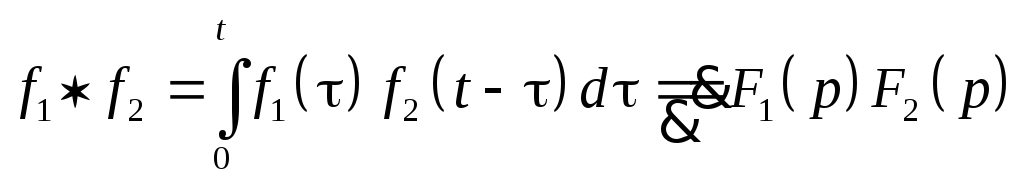
-
Интеграл Дюамеля
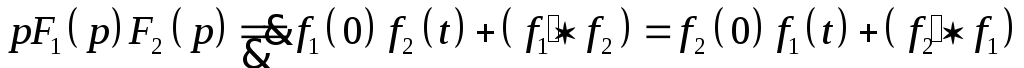
Примеры: Найти изображения функций.
1.
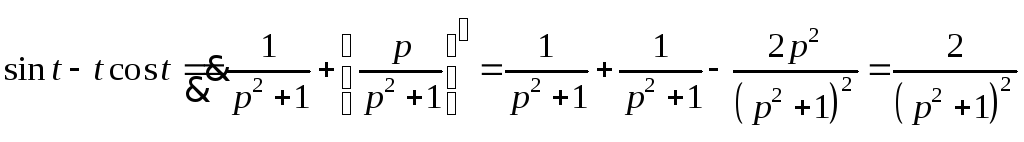 ,
(Re p>0)
,
(Re p>0)
2.
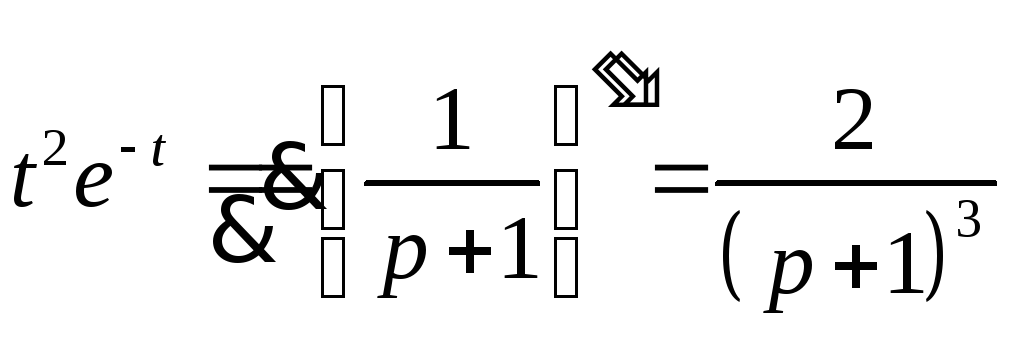 ,
(Re p>-1)
,
(Re p>-1)
-
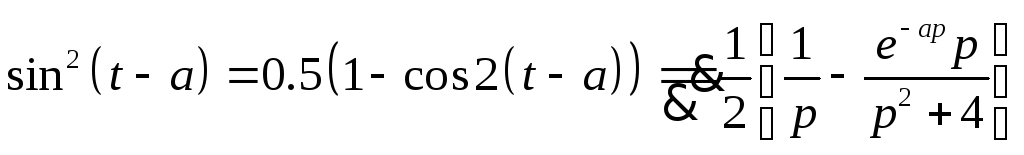 ,
(Re p>0)
,
(Re p>0) -
 ,
(Re p>1)
,
(Re p>1) -
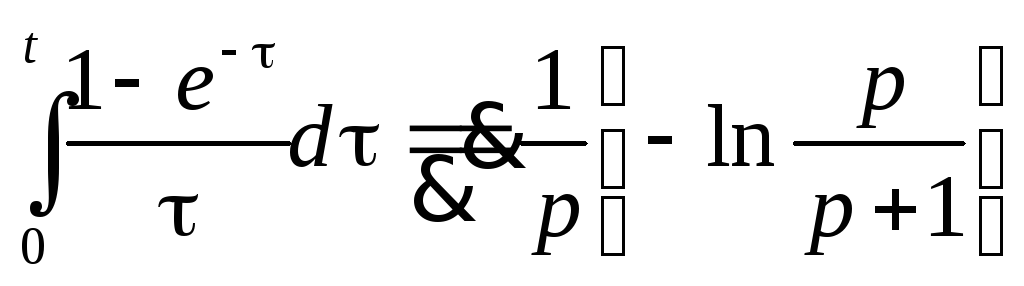 ,
Re p>-1)
,
Re p>-1)
![]() ;
;
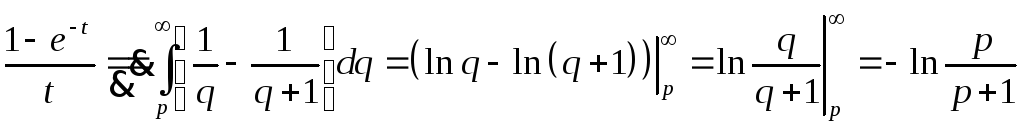
Найти оригиналы изображений.

