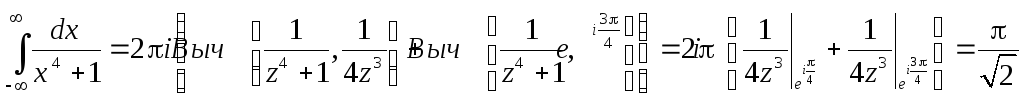Лекции / семестр4 / Лекции МП-2 (Альшина) / Pr3
.doc§26. Вычисление несобственных интегралов I-го рода от функции действительной переменной с помощью вычетов.
-
Лемма1. Несобственные интегралы от быстро убывающих функций.
Лемма
1 Пусть
f(z)C(Imz>0\z1,z2,...,zN)
и |f(z)|<M/|z|1+при
|z|>R0,
>0.
Тогда
![]() ,
где (CR
- полуокружность |z|=R
Imz>0).
,
где (CR
- полуокружность |z|=R
Imz>0).
Доказательство. f(z)C(|z|>R0) и при R>R0:
 .
.
Замечание. Если условия леммы выполнены в каком-либо секторе 1<argz<2, то формула будет иметь место при интегрировании по дуге CR окружности, лежащей в данном секторе.
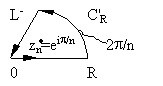
Теорема 26.1. Пусть f(x) задана при -<x< и аналитическое продолжение f(z) на Imz0, имеющее конечное число изолированных особых точек zn, не имеющее особых точек на действительной оси и удовлетворяющее условиям Леммы 26.1.
Тогда
несобственный
интеграл I-го рода
![]() Imzn>0.
Imzn>0.
Доказательство.
При
R>R0
рассмотрим замкнутый контур
(-R<x<R)![]() CR{|z|=R
Imz>0}.
По основной теореме теории вычетов
CR{|z|=R
Imz>0}.
По основной теореме теории вычетов
 Imzn>0.
Imzn>0.
По
Лемме 26.1
![]() ,
правая часть не зависит от R
,
правая часть не зависит от R
![]() Imzn>0.
Imzn>0.
Замечания. 1. Если f(x) - четная (f(-x)=f(x)) и удовлетворяет условиям Теоремы 26.1, то
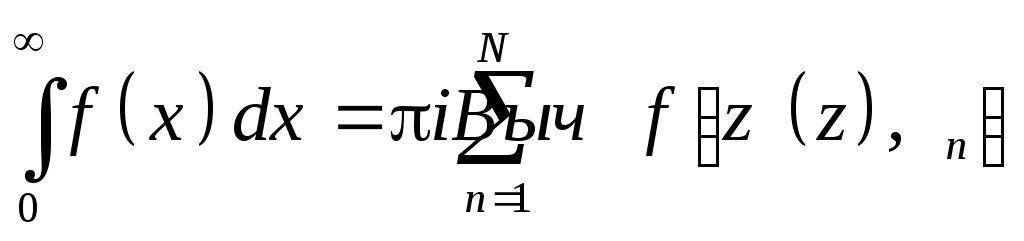 Imzn>0.
Imzn>0.
2. Имеет место аналогичная теорема, когда аналитическое продолжение f(x) в нижнюю полуплоскость удовлетворяет условиям, аналогичным условиям Леммы 26.1 для нижней полуплоскости.
|
Пример. 1.
Особые
точки аналитического продолжения
подынтегральной функции, лежащие в
верхней полуплоскости
2.
|
|
2. Лемма 2 (Лемма Жордана).
Лемма 26.2 (Лемма Жордана). Если f(z)C(Imz>0\z1,z2,...,zN) и f(z)=>0 при |z|(равномерно по argz Imz>0), то при Rea>0
![]()
CR - полуокружность |z|=R Imz>0.
Доказательство .
Разъяснение f(z)=>0 при |z| 0 R: |f(z)|<R, |z|>R, причем R0 при R.
Заметим,
что
![]() ,
при
,
при
![]()

Оценим подынтегральное выражение
![]() ,
при
,
при
![]() .
.
На
контуре интегрирования
![]()
 Замечания.
Замечания.
-
Если f(z) удовлетворяет условиям Леммы Жордана при Imz<0, то при a<0
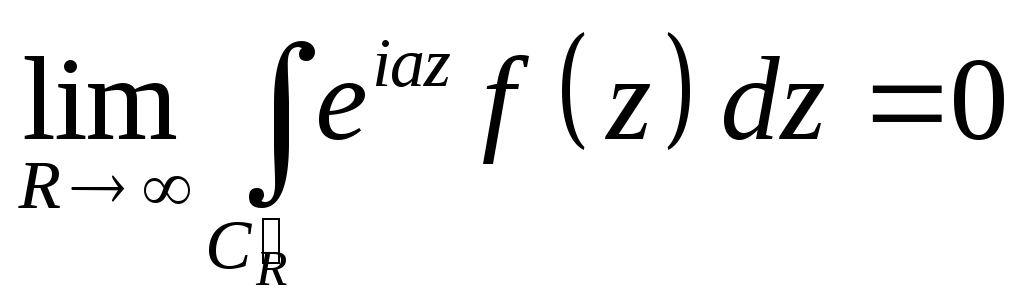 ,
C'R
- полуокружность |z|=R
Imz<0.
,
C'R
- полуокружность |z|=R
Imz<0. -
Если f(z) удовлетворяет условиям Леммы Жордана при Rez>0, то при a=i(>0)
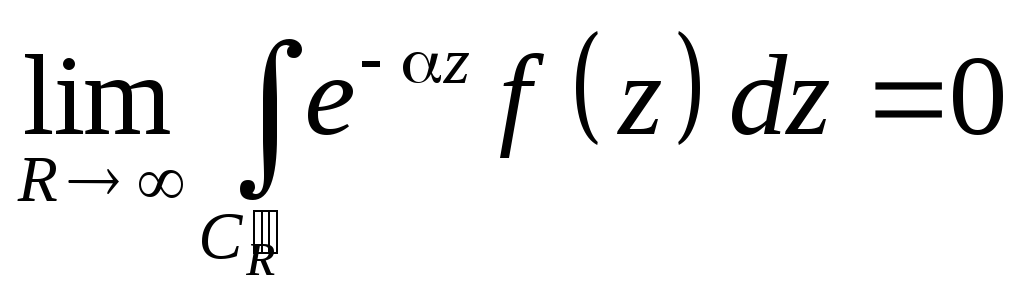 ,
C"R
- полуокружность |z|=R
Rez>0.
,
C"R
- полуокружность |z|=R
Rez>0. -
Если f(z) удовлетворяет условиям Леммы Жордана при Rez<0, то при a=-i(>0)
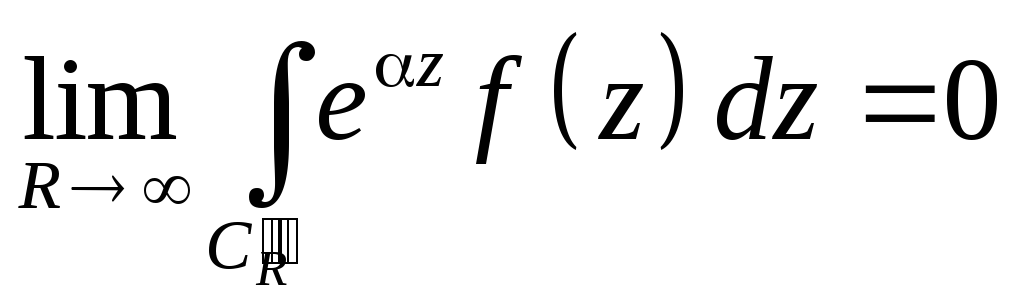 ,
C'"R
- полуокружность |z|=R Rez<0.
,
C'"R
- полуокружность |z|=R Rez<0. -
Лемма Жордана остается справедливой, когда f(z) удовлетворяет условиям Леммы Жордана при Imz>y0 (Rez>x0; Imz<y0; Rez<x0), y0 (x0)- фиксированное число, которое может быть как >0, так и <0, а интегрирование производится по дуге полуокружности |z-iy0|=R Imz>y0 (|z-x0|=R Imz>x0; |z-iy0|=R Imz<y0; |z-x0|=R Imz<x0). Доказательство аналогично, но при оценке интеграла следует сделать замену =Rei+iy0 ( =Rei +x0).
Теорема
26.2
Пусть f(x)
задана при -<x<
и аналитическое
продолжение f(z)
на Imz>0,
имеющее конечное число изолированных
особых точек zk,
не имеющее особых точек на действительной
оси и удовлетворяющее условиям Леммы
Жордана . Тогда при
a>0
![]() Imzk>0.
Imzk>0.
Доказательство.
При R>R0
рассмотрим замкнутый контур
(-R<x<R)
CR{|z|=R
Imz>0}.
По основной теореме теории вычетов
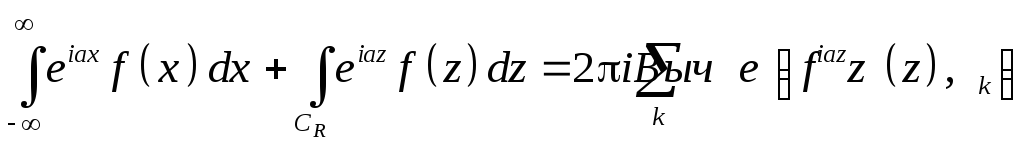 Imzk>0.
Но, по Лемме Жордана
Imzk>0.
Но, по Лемме Жордана
![]() ,
правая часть не зависит от R
,
правая часть не зависит от R ![]() Imzk>0.
Imzk>0.
Замечания.
-
К интегралам данного типа сводятся многие действительные интегралы, содержащие тригонометрические функции. Полезно помнить, что
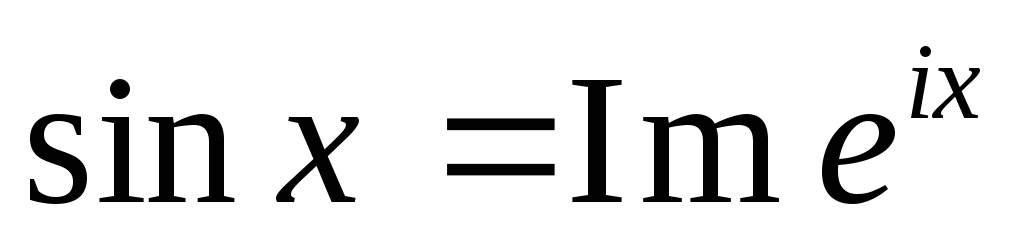 ,
,
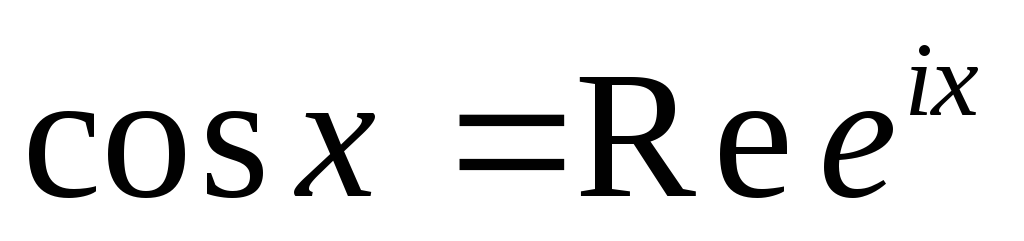
-
Если a<0 и f(z) удовлетворяет условиям Леммы Жордана в нижней полуплоскости, то
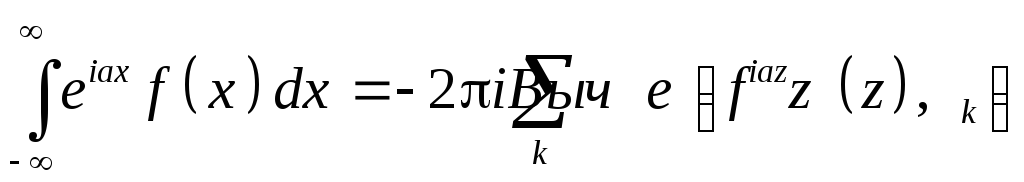 Imzk<0.
Знак меняется из-за изменения направления
обхода контура CR.
Imzk<0.
Знак меняется из-за изменения направления
обхода контура CR.
Примеры.
1.Вычислить интеграл
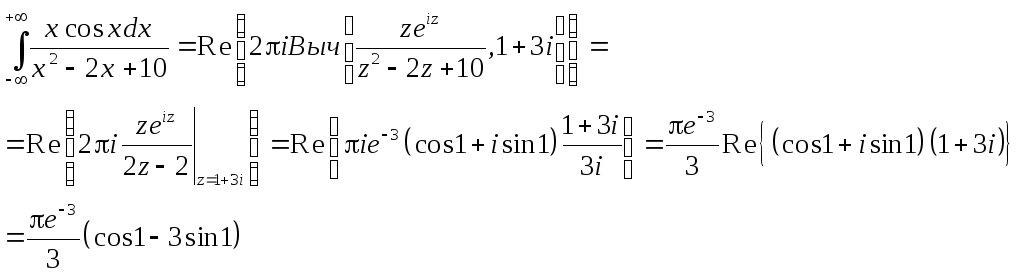
-
Вычислить интеграл
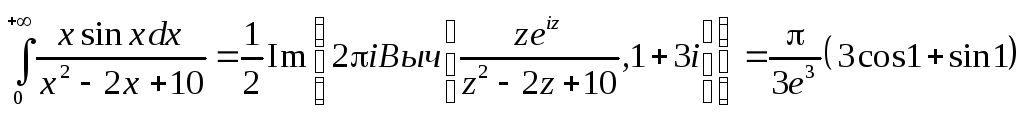
Лемма
2. Пусть
f(z)C(0<|z0-z|<0)
и z0
– полюс первого порядка, тогда
 ,
где (C
- полуокружность |z|=
и 0<arg(z)<
0+).
,
где (C
- полуокружность |z|=
и 0<arg(z)<
0+).
Доказательство.
![]()
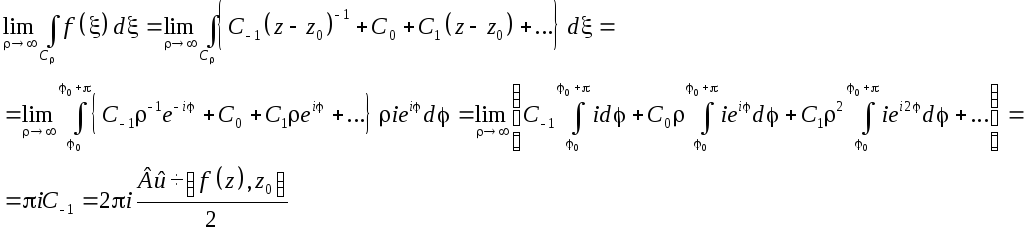
Примеры.
![]()