Лекции / семестр4 / Лекции МП-2 (Альшина) / Pr4

Сходимость несобственных интегралов.

Напомним некоторые определения и теоремы из курса действительного анализа.

Определение. Если функция определена на бесконечном полуинтервале и интегрируема по Риману на любом и - несобственный интеграл 1-го рода.

Если указанный предел не существует, то говорят, что несобственный интеграл расходится.

Для несобственных интегралов верна формула Ньютона-Лейбница. Если существует какая-либо первообразная, то . Т.о. вопрос о сходимости некоторых несобственных интегралов можно решить, вычислив их. Например, сходится при p>1.

Для несобственных интегралов от знакопостоянных функций справедливы признаки сравнения:

Пусть функции f и g неотрицательны на полуинтервале и , тогда

1. если 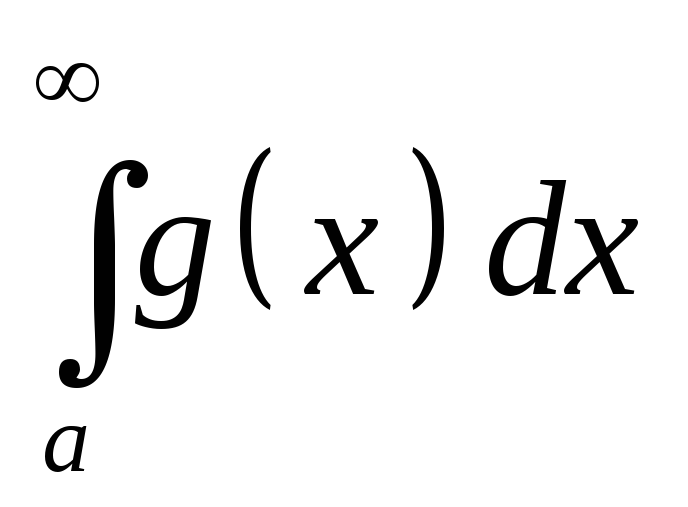сходится, то и тоже сходится,

2. если расходится, то и тоже расходится.

Справедлив и предельный признак сравнения.

Пусть функции f и g положительны на полуинтервале и , тогда несобственные интегралы и сходятся и расходятся одновременно.

Существует понятие абсолютной сходимости несобственного интеграла (сходимость интеграла от модуля функции) и справедлива теорема о том, что из абсолютной сходимости несобственного интеграла следует обычная его сходимость.

Так же, как и для рядов имеет место критерий Коши сходимости несобственных интегралов:

Для сходимости несобственного интеграла необходимо и достаточно, что бы >0 ():  и  .

Для знакопеременных функций справедливы достаточные признаки сходимости Дирихле и Абеля.

Признак Дирихле. Пусть

1. f С и ее первообразная |F(x)|<M x>a,

2. gС¹ g’(x)<0

3. ,

тогда несобственный интеграл сходится.

Доказательство.

При сделанных предположениях f g С, т.о. f g интегрируема на  [a,b]. Проинтегрируем по частям

(*)

Устремим верхний предел к бесконечности.

Т.о. интегралы от неотрицательной функции ограничены по совокупности и т.о. несобственный интеграл сходится абсолютно, а значит .

Тогда , т.е. несобственный интеграл сходится.

Признак Абеля. Если

1. f С и сходится

2. gС¹ ограничена и монотонна,

то несобственный интеграл сходится.

Доказательство.

Интегралы и отличаются лишь знаком и поэтому сходятся и расходятся одновременно, т.о. достаточно доказать сходимость лишь одного из них. g монотонна, значит хотя бы одна их функций g(x) или – g(x) убывает. Пусть для определенности убывает g(x).

В силу ее ограниченности и монотонности , т.е. .

1) сходится, значит и тоже сходится.

2) Кроме того, из чего следует, что ограниченность |F(x)|<M x>a.

Тогда для несобственного интеграла выполнены все условия признака Дирихле и он т.о. сходится.

Следовательно, несобственный интеграл сходится.

Пример.

1. - сходится при p>0 по признаку Дирихле.

2. - сходится при p>0 по Абелю.

Несобственные интегралы, зависящие от параметра.

Рассмотрим интеграл вида

Определение. Если y₀Y несобственный интеграл сходится, то говорят, что несобственный интеграл сходится на множестве Y.

Это означает, чо при каждом фиксированном yY  (,y): >(,y) .

Определение. Сходящийся на множестве Y несобственный интеграл называется равномерно сходящимся на этом множестве, если  (): >() yY .

Пример. сходится равномерно при , но не равномерно при , т.к. остаток этого несобственного интеграла не может быть равномерно ограничен.

Признак Вейерштрасса. Если yY при a<x и несобственный интеграл сходится, то сходится равномерно на множестве Y

Доказательство.

 (): >() yY .

Свойства равномерно сходящихся несобственных интегралов, зависящих от параметра.

Для несобственных интегралов, зависящих от параметра в случае их равномерной сходимости, возможен переход к пределу по параметру под знаком несобственного интеграла, возможно при необходимости проинтегрировать по параметру поменять порядок интегрирования и т.п., но главное:

Теорема (о дифференцировании под знаком несобственного интеграла).

Пусть и . Если сходится, а сходится равномерно, то и .

Доказательство.

Рассмотрим неубывающую последовательность {_n}: a=₁ . Функция представима в виде сходящегося ряда . Тогда функцию можно представить в виде равномерно сходящегося ряда . Ряд сходится равномерно в силу критерия Коши, т.к. все его остатки могут быть равномерно ограничены.

В силу теоремы о почленном дифференцировании равномерно сходящихся рядов действительного переменного

.

Пример.

1. ;

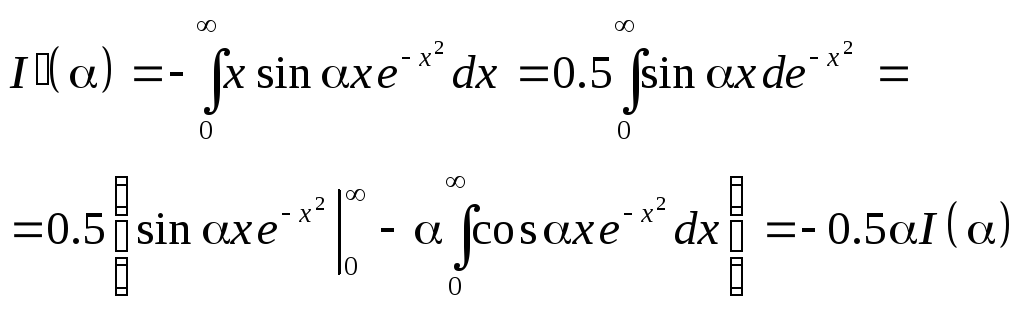
Известно, что , т.о.

2. Интегралы Френеля и .

Замена переменного :

Аналогично,