Лекции / семестр4 / Лекции МП-2 (Альшина) / Pr9

Формальный переход от ряда к интегралу Фурье.

Представление функции суммой ряда из тригонометрических функций справедливо для периодической функции. Что делать если функция непериодическая? Формально ее можно трактовать как функцию с бесконечным периодом. Попробуем обобщить Фурье анализ и на этот случай. Попробуем чисто формально устремить период функции к .

Пусть функция с периодом 2l представима своим рядом Фурье

,

где

, .

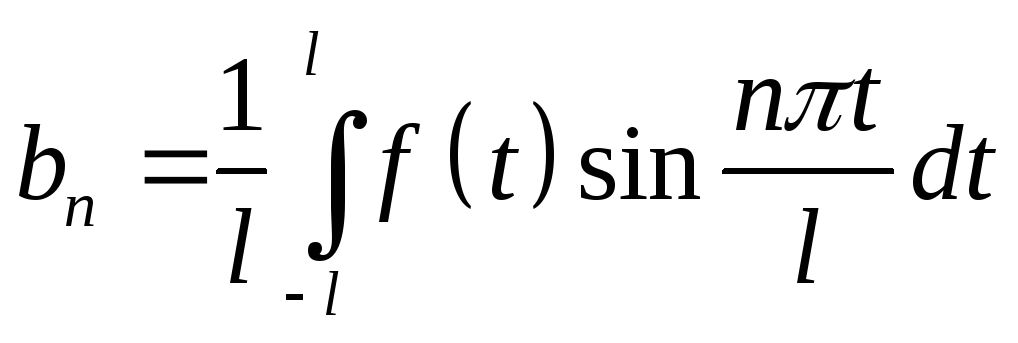Подставим выражения для коэффициентов в ряд Фурье.

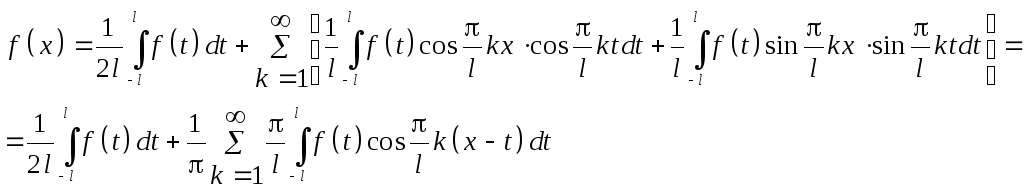Предположим, что функция абсолютно интегрируема на всей числовой прямой , и формально устремим l. При этом первое слагаемое справа 0 (l в знаменателе). А втрое слагаемое можно рассматривать как интегральную сумму для несобственного интеграла 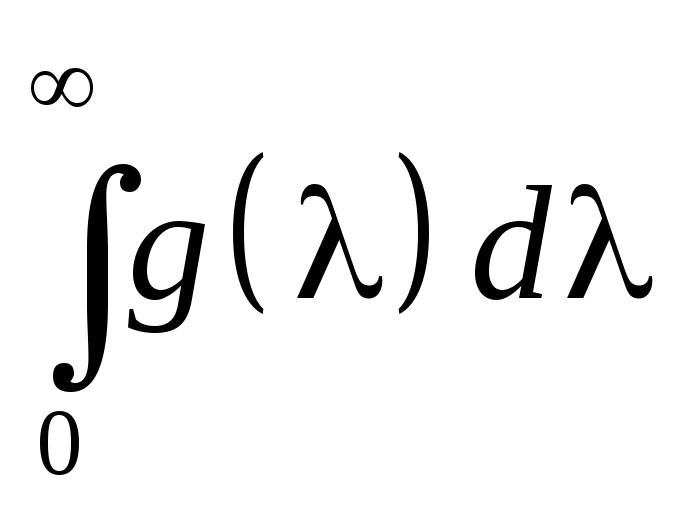для функции 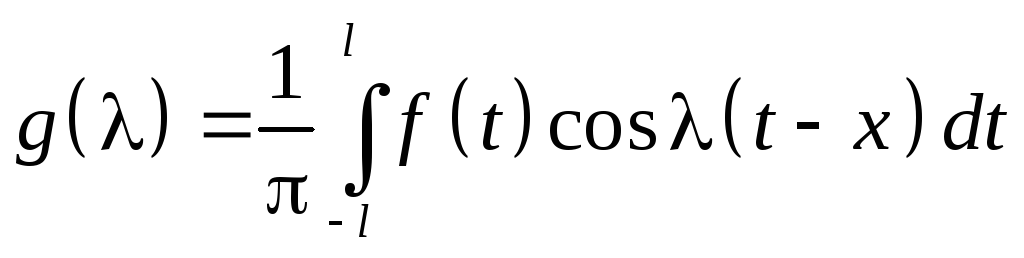. Интегральная сумма берется по точкам и .

Поэтому формальный переход l приводит к и интегральная сумма переходит в интеграл

.

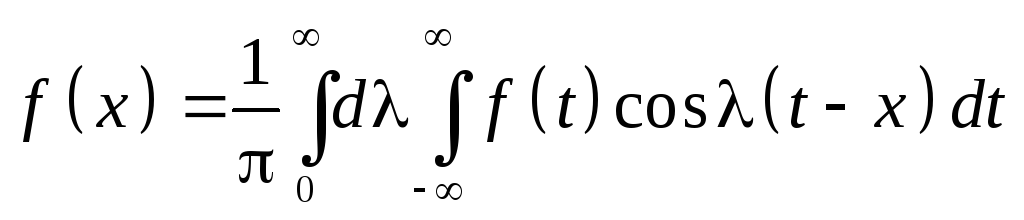Эта формула называется формулой Фурье. Если положить

, ,

то формулу Фурье можно записать в виде

.

§32. Преобразование Фурье и его свойства.

Будем рассматривать функции f(x) – кусочно гладкие на каждом конечном отрезке действительной оси и абсолютно интегрируемые на всей числовой прямой в несобственном смысле ().

Далее речь пойдет о комплеснозначной функции g() действительного переменного . Под этой функцией понимается пара двух действительных функций g()=u()+iv().

Лемма 1. Если f(x) – кусочно гладкая и , то для : (-,) существует несобственный интеграл

,

называемый преобразованием Фурье (образом Фурье) функции f(x). Функция g() непрерывна по  на всей числовой прямой.

Доказательство.

Из очевидного равенства следует, во-первых, существование, а во-вторых, равномерная сходимость (по признаку Вейерштрасса) несобственного интеграла

.

Несобственный интеграл от непрерывной по параметру функции, сходящийся равномерно по параметру представляет собой непрерывную функцию этого параметра.

Лемма 2 (лемма Римана). Пусть f(x) кусочно гладкая на всей числовой прямой и [a,b] – произвольный фиксированный сегмент, тогда

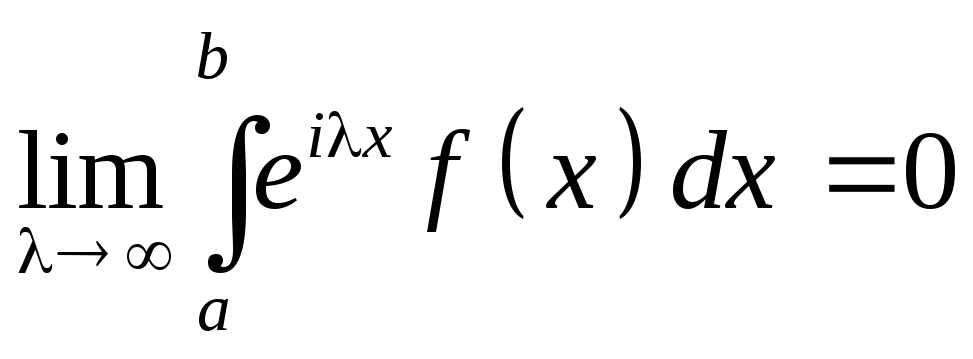, где Real.

Доказательство.

.

Смотри Лемму Лебега и замечание к ней.

Замечание.

Требование кусочной гладкости как и в Лемме Лебега избыточно, его можно заменить локальной интегрируемостью.

Лемма 3. Преобразование Фурье g() от кусочно-гладкой, абсолютно интегрируемой функции стремится к нулю при

.

Доказательство. Возьмем произвольное >0. В силу сходимости несобственного интеграла можно выбрать такое число A>0, что

(остаток сходящегося несобственного интеграла – малое число). Т.е. число A настолько велико, что само значение несобственного отличается от приближенного менее чем на /2

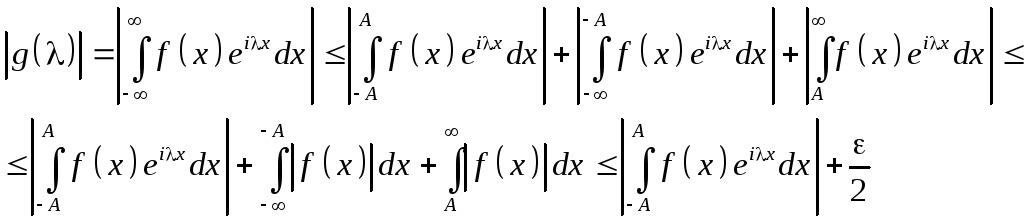
Интеграл в правой части при достаточно большом  может быть оценен сверху числом /2, т.к. по Лемме Риммана, т.к. .

Тем самым для >0 ₀ : >₀ , что и доказывает лемму.

Следствие Леммы 3.

При выполнении условий Леммы 3

и .

Еще один факт, установленный при изучении теории вычетов, необходимо вспомнить для доказательства следующей теоремы.

(a>0)

Доказательство.

.