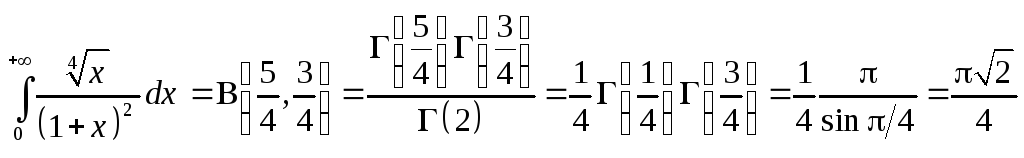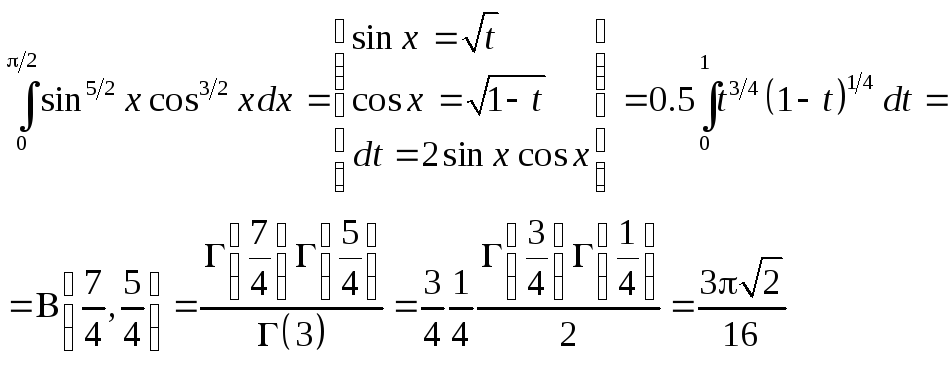Лекции / семестр4 / Лекции МП-2 (Альшина) / Pr5
.docЭйлеровы интегралы.
Определение.
Гамма-функция
![]() и бета-функция
и бета-функция
![]() называются Эйлеровыми интегралами и
играют важную роль в различных разделах
математики и матфизики.
называются Эйлеровыми интегралами и
играют важную роль в различных разделах
математики и матфизики.
Мы остановимся на свойствах первой из этих функций, выраженной несобственным интегралом первого рода, зависящим от параметра.
Свойства гамма-функции:
-
 сходится при
сходится при .
Для того, что бы убедиться в этом разобьем
его на два
.
Для того, что бы убедиться в этом разобьем
его на два
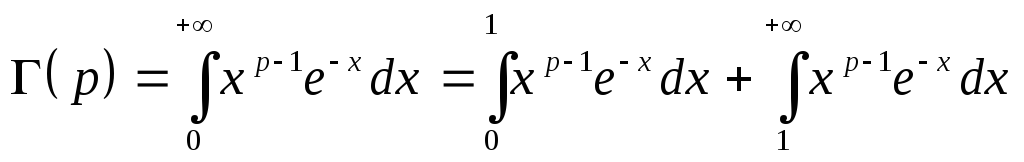 .
Второй интеграл сходится по признаку
сравнения, т.к. подынтегральная функция
убывает быстрее, чем, скажем,
.
Второй интеграл сходится по признаку
сравнения, т.к. подынтегральная функция
убывает быстрее, чем, скажем,
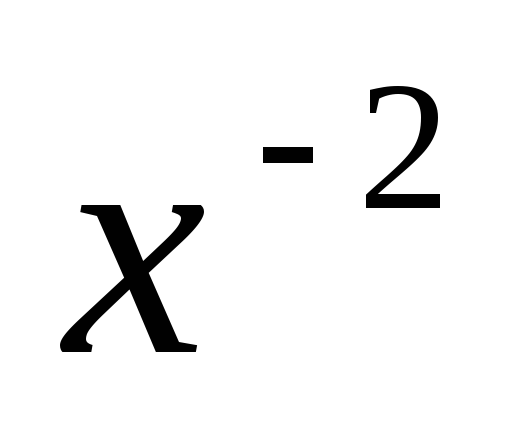 .
Первый интеграл несобственный второго
рода я особой точкой
.
Первый интеграл несобственный второго
рода я особой точкой
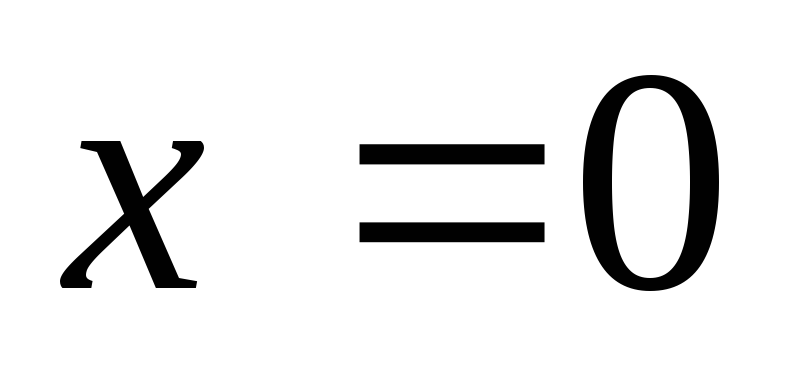 .
Опять же по признаку сравнения, учтя
что
.
Опять же по признаку сравнения, учтя
что
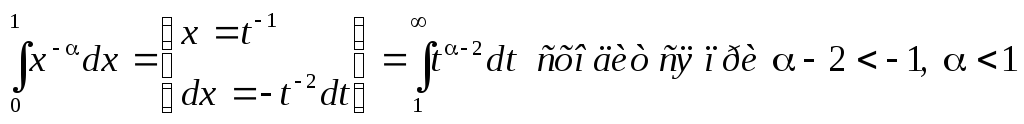
сходится при
![]() .
.
-
Сходится равномерно по p при
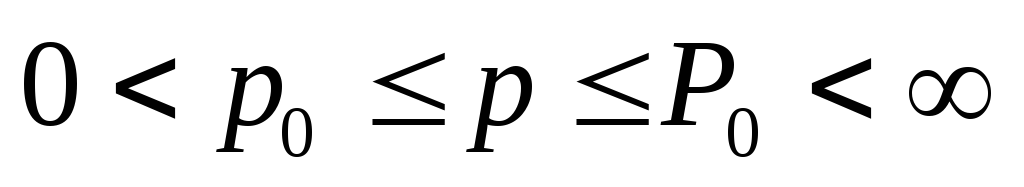 .
Рассмотрим отдельно опять два интеграла.
.
Рассмотрим отдельно опять два интеграла.
1)
![]() при
при
![]() сходимость
равномерная по признаку Вейерштрасса
(мажорирующий интеграл сходится), при
сходимость
равномерная по признаку Вейерштрасса
(мажорирующий интеграл сходится), при
![]() равномерной сходимости нет, т.к. остаток
интеграла
равномерной сходимости нет, т.к. остаток
интеграла
![]() для
фиксированного
для
фиксированного
![]() и
и
![]() .
.
2)
![]() при
при
![]() сходимость равномерная по признаку
Вейерштрасса (мажорирующий интеграл
сходится), при
сходимость равномерная по признаку
Вейерштрасса (мажорирующий интеграл
сходится), при
![]() равномерной сходимости нет, т.к. остаток
интеграла
l>1
каково бы ни было N
– натуральное число при
равномерной сходимости нет, т.к. остаток
интеграла
l>1
каково бы ни было N
– натуральное число при
![]() выполнено p-1>N
выполнено p-1>N
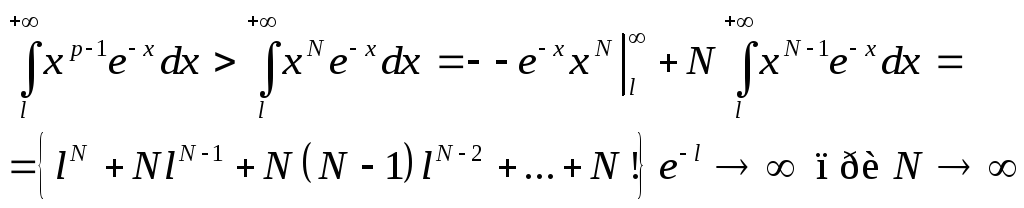
-
Т.к. подынтегральная функция непрерывна, то в области равномерной сходимости несобственного интеграла, т.е. на конечном промежутке
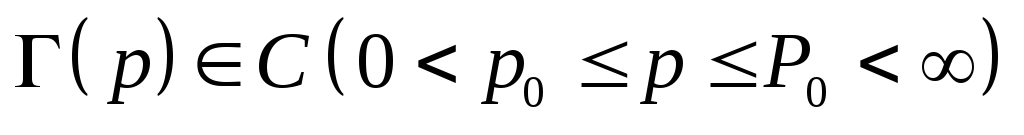 .
. -
Производная гамма-функции может быть вычислена под знаком интеграла
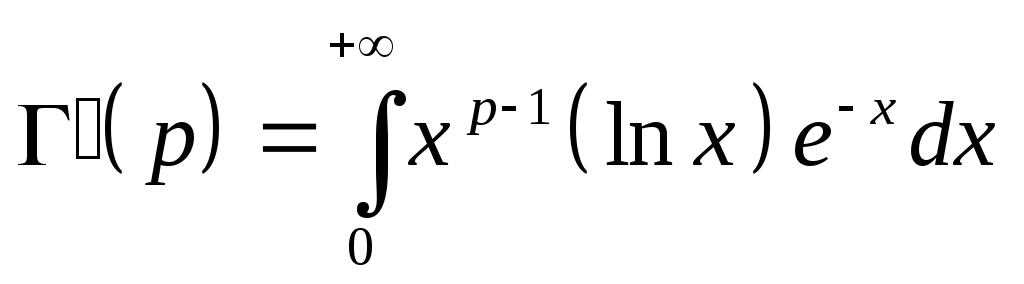 в силу равномерной сходимости интеграла
производной при
в силу равномерной сходимости интеграла
производной при
 .
Действительно,
.
Действительно,
![]()
![]()
Оба интеграла сходятся равномерно по признаку Вейерштрасса.
Аналогично, вычисляются производные гамма-функции любого порядка
![]()
-
Интегрируя по частям, получим
![]() .
.
![]()
В частности, для целочисленных аргументов
![]()
Свойства бета-функции:
-
 сходится
при p>0,
q>0.
сходится
при p>0,
q>0. -
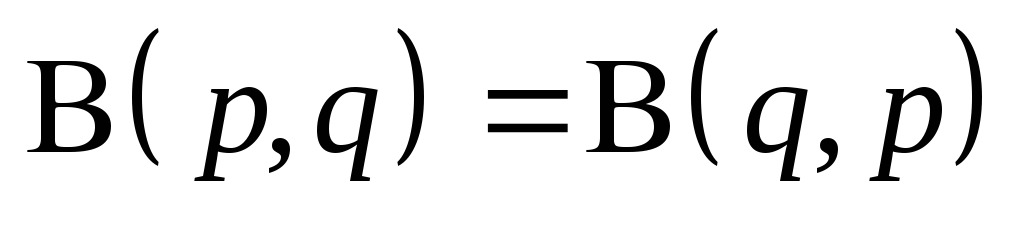 (доказывается
при помощи замены переменной x=1-t).
(доказывается
при помощи замены переменной x=1-t). -

-
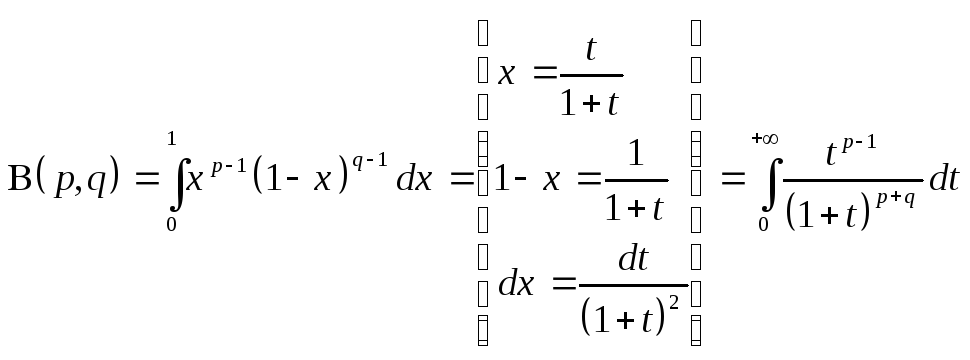
-
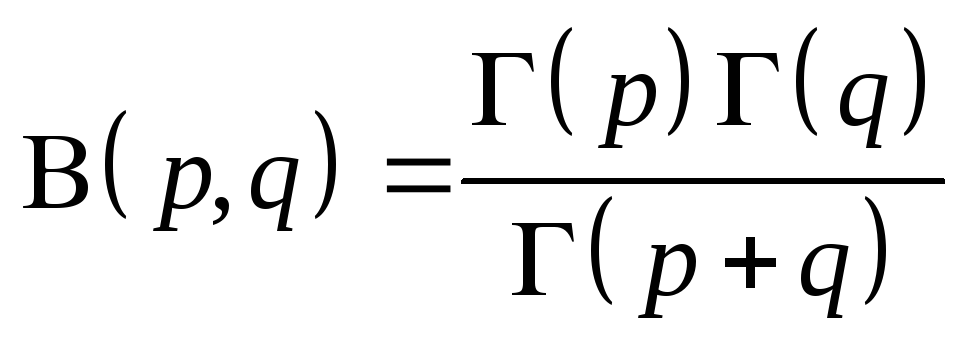
Доказательство.
![]()
![]() ,
аналогично
,
аналогично
![]()
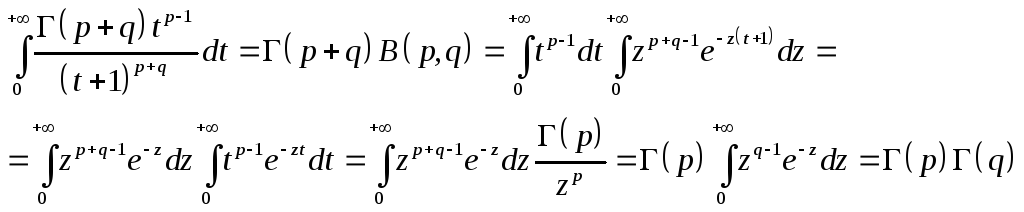
-
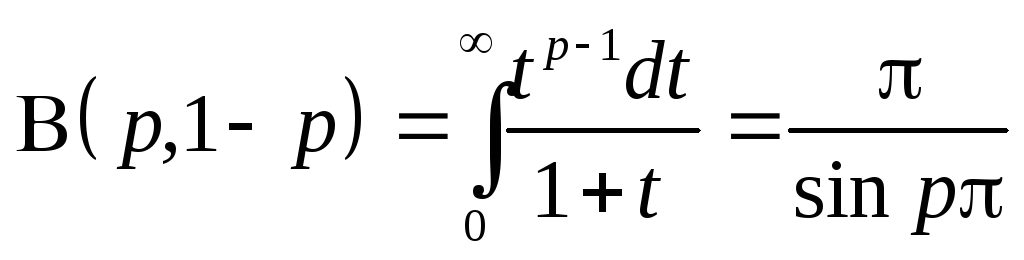
 (интеграл
берется вычетами).
(интеграл
берется вычетами).
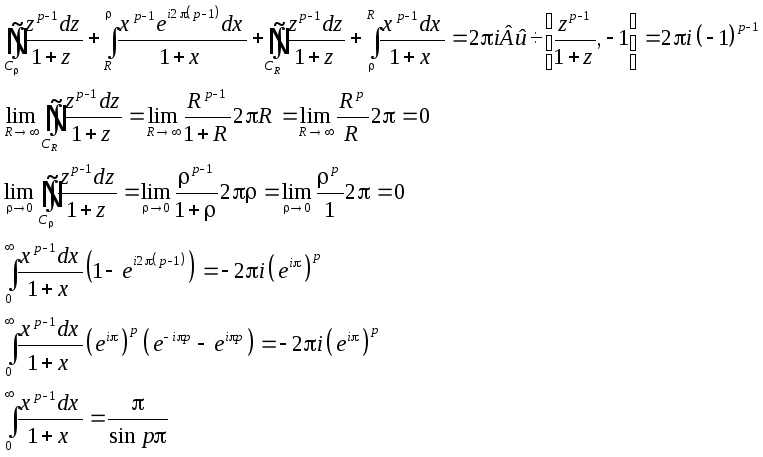
![]()
-
 формула дополнения.
формула дополнения.
Примеры.