§35. Методы математической физики (ММФ).

Уравнениями математической физики принято называть линейные дифференциальные уравнения в частных производных второго порядка. Рассмотрим здесь простейший случай линейного уравнения с постоянными коэффициентами для функции двух переменных.

Такие уравнения путем замены переменных могут быть приведены к каноническому виду

Канонический вид	Тип уравнения	Физическая интерпретация
	параболический	уравнение теплопроводности, диффузии
	гиперболический	уравнение колебаний, волновое уравнение
	эллиптический	стационарные процессы, установившиеся распределения

При нетривиальной правой части уравнения называются неоднородными, они описывают поведение систем под воздействием внешних факторов. В противном случае уравнения однородные.

Для выделения единственного решения задачи для дифференциального уравнения необходимы дополнительные условия. Условия, поставленные при t=0, называются начальными. Условия, поставленные на границе области изменения пространственной переменной, называют граничными или краевыми. Эти условия так же могут быть однородными и неоднородными.

Будем рассматривать задачи в прямоугольной области изменения переменных .

Будем рассматривать линейные краевые условия, они для уравнения второго порядка могут быть одного из следующих трех типов (приведены однородные граничные условия, т.к. в этом курсе другие не будут рассмотрены).

	условие 1-го рода или Дирихле
	условие 2-го рода или Неймана
	условие 3-го рода

Для задач математической физики доказаны теоремы существования и единственности решения. Задача для однородного уравнения с однородными дополнительными условиями имеет только тривиальное решение. Неоднородные задачи в силу линейности допускают редукцию к более простым задачам. Т.о. имеет смысл рассматривать задачи неоднородные либо только по правой части уравнения, либо по только начальным, либо только по граничным условиям. Решение произвольной задачи, очевидно, является суммой решения этих трех.

Уравнения, приведенные к каноническому виду, допускают разделение переменных, т.е. решение можно искать в виде . И решение таких задач находится при помощи метода Фурье.

Мы рассмотри 4 типа задач.

§35. Однородное уравнение колебаний с неоднородными начальными условиями.

,,

,

Мы взяли для определенности граничное условие Дирихле на левой границе и условие Неймана - на правой и конкретизировали начальные условия, по ходу изложения станет понятно, что метод универсален и не зависит от этого выбора.

Разделение переменных приводит к равенству, обе части которого зависят лишь от одной переменной, это возможно лишь тогда, когда обе они равны константе

Для пространственной части, получаем так называемую задачу Штурма-Лиувилля (граничные условия могут быть и другого вида, но обязательно однородные)

.

Нетривиальные решения задачи Штурма-Лиувилля существуют лишь при определенных значениях , называемых собственными значениями задачи Ш-Л. Эти решения называются собственными функциями задачи Ш-Л и образуют ортогональную систему функций, являющуюся базисом в пространстве решений исходной задачи. Согласно теореме Стеклова, при определенных условиях на гладкость произвольная функция может быть разложена в ряд Фурье по ортогональной системе функций. В данном курсе будут рассмотрены начально-краевые задачи на отрезке, где в качестве системы СФ задачи ШЛ всегда в таких задачах возникает тригонометрическая система. Для разложения в ряд Фурье по этой системе достаточно, как было показано, кусочной гладкости.

Общее решение этой задачи имеет вид

.

Из граничных условий находим допустимые значения 

 A=0

 , n=1,2,3,…

Т.о. найдены собственные значения и собственные функции задачи Ш-Л .

Подчеркнем, что СЗ и СФ однозначно определены для этого уравнения типом граничных условий, другие граничные условия дали бы другие СФ и СЗ, найти которые не составляет труда в каждом конкретном случае.

Подставим найденное  в уравнение для временной части

Его решение

.

Неизвестные коэффициенты A_n, B_n найдем из начальных условий

.

Решение исходной задачи может быть представлено своим рядом Фурье по ортогональной системе СФ задачи Ш-Л

, .

Т.о. коэффициенты A_n, B_n находятся из Фурье разложения начальных условий по СФ задачи Ш-Л. Для нахождения такого разложения помножим обе части равенства на СФ и проинтегрируем

.

В силу ортогональности СФ задачи Ш-Л в правой части останется только коэффициент A_m помноженный на квадрат нормы СФ

.

Аналогично для B_m

Заметим, пока вид СФ не конкретизировался, т.е. метод подойдет для любого вида СФ и общее решение однородного уравнения колебаний с неоднородными начальными условиями

, где , .

Применительно к рассматриваемой задаче с конкретными начальными и граничными условиями

.

,

.

Т.о. решение исходной задачи

§36. Неоднородное уравнение колебаний с однородными начальными условиями.

,,

,

Попробуем искать решение этой задачи опять при помощи разложения в ряд Фурье по СФ задачи Ш-Л. Рассмотрим для начала однородное уравнений, проведем в нем разделение переменных, для пространственной части получим опять задачу Ш-Л, которая в случае данных краевых условий имеет вид

.

Ее СФ и СЗ .

Т.о. . Подставим в исходное уравнение, разложив функцию в правой части так же в ряд Фурье по системе СФ задачи Ш-Л :

Из задачи Ш-Л найдем , тогда

,

приравнивая слагаемые при одинаковых базисных функциях, получим ОДУ для временной части решения

.

Общее решение такого ОДУ второго порядка имеет вид

.

Учитывая нулевые начальные условия

,

находим недостающие коэффициенты A_n, B_n

; .

Т.о. для временной части

.

Общее решение начально-краевой задачи для неоднородного уравнения колебаний с однородными начальными условиями

, где

Т.о. решение исходной задачи

Заметим, что до сих пор вид СФ и правой части уравнения не конкретизировался, следовательно, проведенные выкладки универсальны.

Вспомним теперь конкретный вид краевых условий (а, следовательно, и СФ) и правой части уравнения

.

.
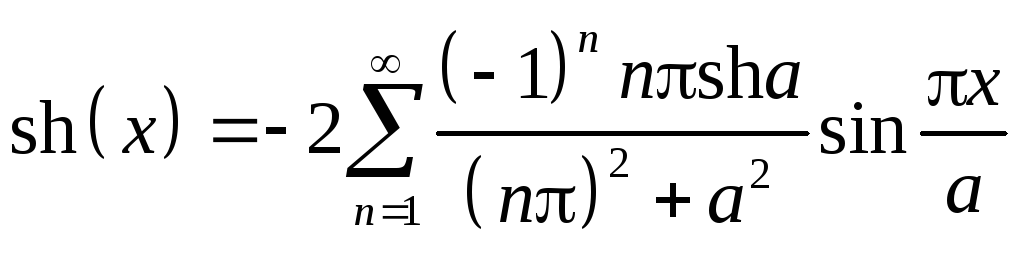
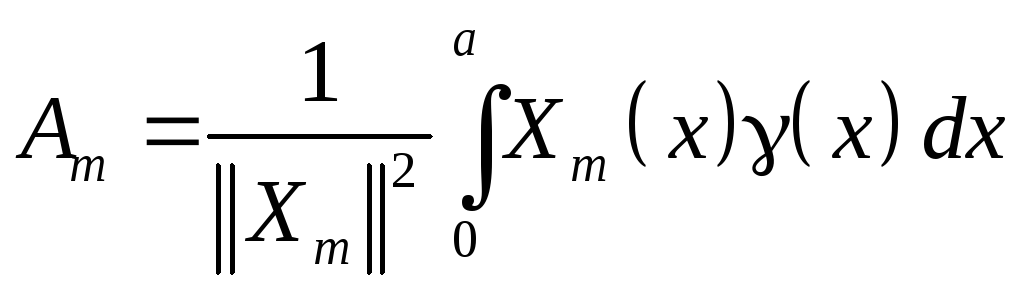