6. Исследование решения задач линейного программирования

6.1. Двойственность задач линейного программирования

Задачи ЛП обладают очень важным свойством двойственности, которое заключается в следующем.

Если существует исходная задача нахождения максимума целевой функции F, то существует и двойственная к ней задача нахождения минимума функционала Ф:

(6.1)

где y_i – переменные двойственной задачи.

Существует правило перехода к двойственной задаче, заключающееся в следующем:

1. j-й столбец, составленный из коэффициентов ограничения исходной задачи, совпадает с j-й строкой, составленной из коэффициентов ограничений двойственной задачи.

2. Строка, составленная из коэффициентов целевой функции, совпадает со столбцом, составленным из констант правых частей ограничений двойственной модели.

3. Столбец, составленный из констант правых частей ограничений исходной модели, совпадает со строкой, составленной из коэффициентов целевой функции двойственной задачи.

4. Направление знаков неравенства в исходной модели противоположно направлению знаков неравенства в двойственной задаче.

5. Требование максимизации (или минимизации) в исходной задаче заменено требованием минимизации (или максимизации) в двойственной задаче.

(6.2)

Двойственная задача, сформулированная из чисто математических соображений, оказывается, тесно связана с прямой (исходной) задачей ЛП. В частности, равенствам прямой задачи соответствуют переменные двойственной задачи, неограниченные в знаке, и, наоборот, с равенствами двойственной задачи соотносятся переменные прямой задачи, неограниченные в знаке:

Пример.

F=4x1+5x2+9x3max, x1+x2+2x3=16, 7x1+5x2+3x325, x10, x20, x3 неограниченно в знаке

Ф=16y1+25y2min, 1y1+7y24, 1y1+5y25, (6.3) 2y1+3y2=9, y20, y1 неограниченно в знаке

Понятие двойственности имеет большое значение в исследовании операций благодаря свойствам, сформулированным в теореме двойственности, которая утверждает:

А. Если исходная и двойственная ей задачи имеют допустимые решения, то:

1. существует оптимальное решение исходной задачи;

2. существует оптимальное решение двойственной задачи ;

3. при оптимальных значениях переменных максимум целевой функции одной задачи равен минимуму целевой функции двойственной задачи:

. (6.4)

В. Если исходная задача допускает оптимальное решение, для которого значение целевой функции ограничено, то соответствующая двойственная задача допускает оптимальное решение при том же значении целевой функции.

Иначе говоря, если существует оптимальное решение одной задачи, то должно существовать оптимальное решение и двойственной ей задачи.

Не приводя математического доказательства всех утверждений, составляющих в совокупности теорему двойственности, имеет смысл остановиться на некоторых следствиях этой теоремы.

Следствие 1. Можно показать, что любое допустимое решение исходной задачи линейного программирования накладывает ограничение на оптимальное значение целевой функции соответствующей двойственной задачи.

Пусть x_j и y_i удовлетворяют ограничениям, каждая в своей задаче. Умножим каждое i-е уравнение исходной задачи на y_i, а каждое j-е ограничение двойственной задачи на x_j. Т.к. y_i 0 и x _j0, то направление неравенств не изменится:

.

Теперь сложим почленно левые и правые части по :

(6.5)

Аналогично для двойственной задачи.

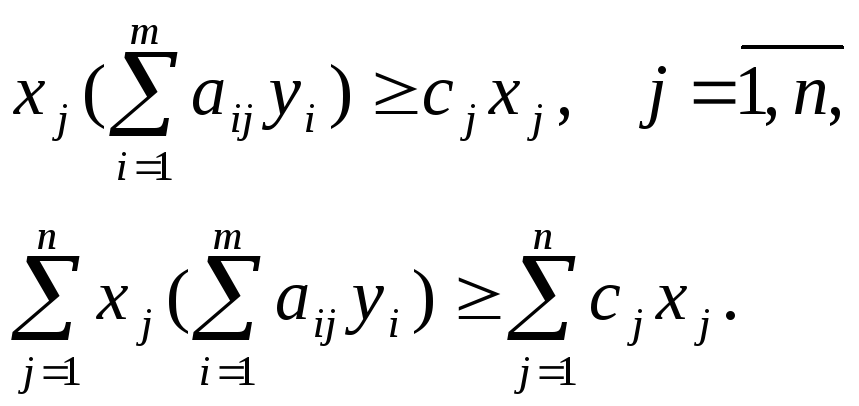(6.6)

Правые части находятся в соотношениях:

или F Ф. (6.7)

Следовательно, из соотношения (6.7) видно, что значение целевой функции, соответствующее некоторому допустимому (включая оптимальное) решению исходной задачи, зависит и ограничивается значением целевой функции для любого допустимого решения (включая оптимальное) соответствующей двойственной задачи.

Например, для записанных ранее исходной и двойственной задач (6.3) следует, что допустимыми решениями их могут быть x₁=x₂=0, x₃=8 и y₁=0, y₂=3, поэтому целевые функции будут находиться в соотношениях

4x₁ + 5x₂ + 9x₃  16y₁ +25y₂.

Подставив допустимые решения, получим F=72, Ф=75.

В соответствии со следствием 1 можно утверждать, что оптимальное значение целевой функции, как для исходной, так и для двойственной задачи, лежит в интервале от 72 до 75.

Из теоремы двойственности можно вывести следствие 2.

Для допустимых решений прямой и двойственной задач можно записать ограничения-неравенства

(6.8) и . (6.9)

Если умножить (6.8) на , а (6.9) на, при этом оба эти неравенства должны соблюдаться, то для оптимальных значений они превращаются в равенства

, (6.10)

откуда следует, что если (т.е. 0), тогда ;

если (т.е. 0), тогда .

Таким образом, следствие 2 утверждает, что если одна из задач содержит ограничение, имеющее вид строгого неравенства (>,<), то соответствующая переменная в двойственной задаче принимает нулевое значение.