Практикум 2

1

Дистанционный курс « Теория вероятностей»

Практикум №2 «Случайные события. Классическое определение вероятности. Геометрическая вероятность».

Задача 1. Игральный кубик подбрасывается дважды. Наблюдаемый результат – пара чисел, соответстующих числам очков, выпавших в первый и второй раз. События: A={оба раза выпало число очков, кратное трем}, B={оба раза выпало одинаковое число очков}. Построить множество элементарных исходов Ω данного эксперимента и подмножества, соответствующие указанным событиям.

Решение. Множество элементарных исходов состоит из 36 исходов: Ω={(1,1),(1,2),…,(2,1),(2,2),…,(6,1),(6,6)}. Согласно условию задачи, события A и B состоят из следующих элементарных исходов:

A={(3,3),(3,6),(6,3)(6,6)}; B={(1,1),(2,2),(3,3),(4,4),(5,5),(6,6)}.

Задача 2. Монета подбрасывается трижды. Наблюдаемый результат – появление герба (г) или цифры (ц) на верхней стороне монеты. События: A={герб выпал ровно один раз}, B={ни разу не выпала цифра}. Построить множество элементарных исходов Ω данного эксперимента и подмножества, соответствующие указанным событиям.

Решение. Множество элементарных исходов состоит из 8 исходов:Ω={(г,г,г),(г,г,ц),(г,ц,г),(г,ц,ц),(ц,г,г),(ц,г,ц),(ц,ц,г),(ц,ц,ц)}. Тогда согласно условию задачи, события A и B состоят из следующих элементарных исходов:

A={(г,ц,ц),(ц,г,ц),(ц,ц,г)}; B={(г,г,г)}.

Практикум №2 « Случайные события. Классическое определение вероятности. Геометрическая вероятность»

2

Задача 3. Стрелок производит три выстрела по мишени. Событие A состоит в том, что стрелок попал при i-ом выстреле, i=1,2,3. С помощью операций над событиями через данные события выразить следующие события: A= {стрелок попал хотя бы один раз}, B= {стрелок попал не более одного раза},

C= {стрелок попал три раза}.

Решение. Событие A наступает тогда и только тогда, когда наступает A или A , или A . Это означает, что A = A +A +A . Событие B наступает в том случае, если стрелок трижды промахнется или попадет только при каком-то одном выстреле, то есть B=A1 ∙A ∙A +A ∙A ∙A +A ∙A ∙A +A ∙A ∙A .

Аналогично получаем, C = A ∙A ∙A .

Задача 4. В ящике находятся детали трех сортов. Наудачу извлекают одну деталь. Что представляют собой следующие события: A+B,A+C,A∙C,A∙B+C, если событие A={извлечена деталь первого сорта}; B={извлечена деталь второго сорта}; C={извлечена деталь третьего сорта}?

Решение. A+B – это событие, которое происходит при наступлении хотя бы одного из событий A и B, Следовательно, A+B в данном случае – деталь первого или второго сорта. Поскольку A+C – это деталь первого или третьего сорта, то противополож-

ное этому событие A+C – деталь второго сорта. A∙C - невозможное событие, так как деталь не может быть одновременно и первого и третьего сорта. A∙B+C– это сумма невозможного события и события C, то есть событие C, значит событие A∙B+C – деталь третьего сорта.

Задача 5. На карточках написаны натуральные числа от 1 до 30. Наудачу извлекается карточка. Найти вероятность, что число, написанное на карточке будет кратным 5.

Практикум №2 « Случайные события. Классическое определение вероятности. Геометрическая вероятность»

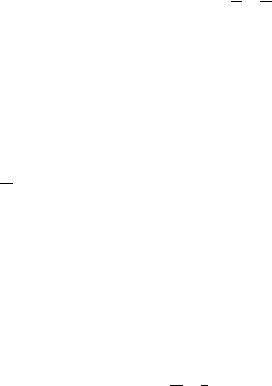
3

Решение. В данном испытании 30 элементарных исходов – любая карточка из 30-ти; событие A={на карточке число, кратное пяти}. Элементарных исходов, благоприятствующих событию A, - 6 – это выпадение 5,10,15,20,25,30. Тогда, по классическому

определению вероятности получаем P(A) = = = 0,2 .

Задача 6. Найти вероятность того, что в наудачу выбранном двузначном числе цифры одинаковы.

Решение. Двузначными числами являются числа от 10 до 99, их всего 90, значит исходов, соответствующих данному испытанию 90.Событие A={выбранное число состоит из одинаковых цифр}, одинаковые цифры имеют 9 чисел – это 11,22,33,44,55,66,77,88, 99, то есть исходов, благоприятствующих событию A- 9, тогда

P(A) = = 0,1.

Задача 7. Бросают два игральных кубика и подсчитывается сумма очков на верхних гранях. Найти вероятность того, что сумма выпавших очков больше девяти.

Решение. Данному испытанию соответствует 36 элементарных исходов. Пусть событие B={сумма очков, выпавших на двух кубиках, больше 9}, больше 9 – это значит либо 10, либо 11, либо 12. Элементарными исходами, благоприятствующими данному событию, являются исходы (4,6),(6,4),(5,5),

(5,6),(6,5),(6,6), их 6, тогда P(B) = = ≈ 0,17.

Задача 8. На пяти карточках написаны буквы А,В,Н,Е,С. Карточки извлекают наудачу по одной и выкладывают в ряд. Найти вероятность того, что получится слово « ВЕСНА».

Практикум №2 « Случайные события. Классическое определение вероятности. Геометрическая вероятность»

4

Решение. Из пяти различных элементов можно составить =5!=120 перестановок, значит всего элементарных исходов,

соответствующих данному испытанию, 120. Пусть событие C = {получится слово «ВЕСНА»}. Исходов, благоприятствую-

Задача 9. Имеется шесть карточек, на которых написаны буквы: на двух буква А, на двух – Т, на одной – Л, на одной – Н. Наудачу извлекают карточки и выкладывают в ряд. Найти вероятность, что получится слово «ТАЛАНТ».

Решение. Так как множество содержит одинаковые элементы, то перестановки этих элементов – это перестановки с повторениями, поэтому число элементарных исходов, соответствующих данному испытанию вычисляется по формуле P (1,1,2,2) =

= ! !!! ! = 180. Пусть событие А ={получится слово «ТА-

ЛАНТ»}. Исходов, благоприятствующих этому событию, всего

один, поэтому P(A) = ≈ 0,006.

Задача 10. Среди 25 студентов группы, в которой 10 девушек, разыгрывается 5 билетов. Найти вероятность того, что среди обладателей билетов окажутся 2 девушки.

Решение. Число всех возможных случаев распределения 5 биле-

лей билетов 2 девушки}. Так как юношей в группе 15, то число

правилу умножения, число исходов, благоприятствующих собы-

Практикум №2 « Случайные события. Классическое определение вероятности. Геометрическая вероятность»

Задача 11. В ящике находятся 15 красных, 9 синих и 6 зеленых шаров. Наудачу вынимают 6 шаров. Найти вероятность того, что среди извлеченных шаров 3 красных, 2 синих и 1 зеленый. Решение. Всего в ящике 30 шаров. Число исходов, соответству-

считаем число исходов, соответствующих данному событию.

Задача 12. В кондитерской продается 7 видов пирожных. Покупатель выбил чек на 4 пирожных. Найти вероятность того, что покупатель заказал пирожные разных видов.

Решение. Покупка 4 пирожных – это сочетание с повторениями, так как в наборе могут быть одинаковые пирожные, следова-

Практикум №2 « Случайные события. Классическое определение вероятности. Геометрическая вероятность»

6

бами, это число исходов, благоприятствующих данному собы-

Задача 13. В лифт девятиэтажного дома на первом этаже вошли 5 человек. Каждый из них с одинаковой вероятностью может выйти на любом этаже, начиная со второго. Найти вероятности следующих событий: A= {все выйдут на одном этаже}, B= {все выйдут на разных этажах}.

Решение. Так как пассажиры могут выйти на одном этаже, то исход испытания – это размещение с повторениями, поэтому число всех исходов равно . Число этажей, на которых могут выйти пассажиры 8, поэтому число исходов, благоприятствую-

Теперь найдем число исходов, благоприятствующих событию B: так как все должны выйти на разных этажах, то данный способ расположения объектов – это размещение, значит число исхо-

дов, благоприятствующих событию B - A , тогда

Задача 14. В некоторой точке C линии OB длины 50 м произошел разрыв. Найти вероятность того, что точка C удалена от точки O на расстояние не меньше 20 м.

Решение. Точки отрезка OB – это точки, соответствующие всем исходам испытания, пусть событие A={точка C удалена от точ-

Практикум №2 « Случайные события. Классическое определение вероятности. Геометрическая вероятность»

7

ки O на расстояние не меньше 20 м}, тогда точки отрезка DB (рис.1) – это точки, соответствующие событию A.

Рис.1

P(A)= |DB|/|OB|=(50-20)/50=30/50≈0,6.

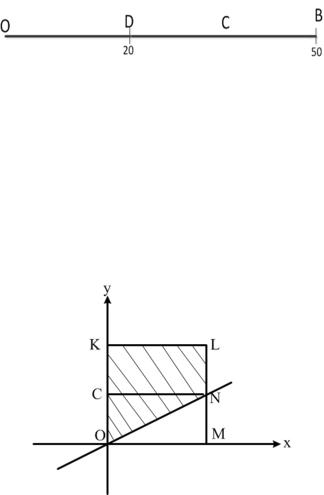
Задача 15. В квадрат (рис.2) с вершинами в точках O(0,0),K(0,1), L(1,1),M(1,0) наудачу поставлена точка P(x,y). Найти вероятность того, что координаты этой точки удовлетворяют неравен-

ству y>1/2 x.

Решение. Пусть событие A={координаты точек удовлетворяют неравенству y>1/2 x }.

Рис.2

Практикум №2 « Случайные события. Классическое определение вероятности. Геометрическая вероятность»

8

Проведем прямую y=1/2 x, она пересечет отрезок ML в точке N(1,1/2). Эта прямая разделит плоскость на две полуплоскости: для координат точек первой из них (верхней) будет выполняться неравенство y>1/2 x, для второй (нижней) – неравенство y<1/2 x.

Все точки, принадлежащие квадрату, - это точки, соответствующие всем исходам испытания, а точки квадрата, координаты которых удовлетворяют неравенству y>1/2 x, то есть точки четырехугольника OKLN – это точки, соответствующие событию A. Вероятность события A вычислим, используя геометриче-

Задача 16. Два парохода должны подойти к одному и тому же причалу. Время прихода обоих пароходов независимо и равновозможно в течение данных суток. Найти вероятность того,что одному из пароходов придется ожидать освобождения причала, если время стоянки первого парохода 1 час, а второго – 2 часа. Решение. Обозначим через x и время прибытия пароходов.

Возможные значения x и y:

0 ≤ x ≤ 24,0 ≤ y ≤ 24

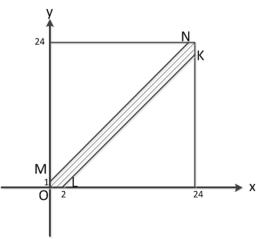
Пусть событие A={одному из пароходов придется ожидать освобождения причала}, тогда координаты точек, соответствующих данному событию, будут удовлетворять неравенствам: y −x ≤ 1,x −y ≤ 2

Эти неравенства определяют область, зашрихованную на рис.3.

Практикум №2 « Случайные события. Классическое определение вероятности. Геометрическая вероятность»

9

Рис.3

Пусть S1 - это площадь квадрата, S1 =24∙24 = 576, S2 - это площадь зашрихованной области, тогда S2 = 24∙24 - 0,5∙23∙23 -

- 0,5∙22∙22=69,5.

P(A) = S2/S1=69,5/576≈0,121.

Задачи для самостоятельного решения.

1.Испытание – подбрасывание двух монет. Составить множество всех исходов, соответствующих данному испытанию, и найти исходы, соответствующие следующим событиям: A={выпал один герб}, B={выпала хотя бы одна цифра}.

2.Пусть A,B,C – три произвольных события. Найти выражения для следующих событий: а) произошло только событие A; б) произошло хотя бы два события; в) ни одно событие не произошло.

3.Наудачу выбрано натуральное число, не превосходящее 15. Найти вероятность того, что оно простое.

Практикум №2 « Случайные события. Классическое определение вероятности. Геометрическая вероятность»

10

4.Подбрасывают две симметричные монеты. Найти вероятность того, что на обеих монетах выпали цифры.

5.В партии из 10 деталей 7 стандартных. Найти вероятность того, что среди 6 взятых наудачу деталей 4 стандартные.

6.На пяти одинаковых карточках написаны буквы: на двух карточках – «л», на двух – «и», на одной – «я». Выкладывают наудачу эти карточки в ряд. Найти вероятность того, что получится слово «лилия».

7.В лифт шестиэтажного дома вошли 4 человека. Каждый из них с одинаковой вероятностью может выйти на любом этаже, начиная со второго. Найти вероятность того, что они все выйдут на 4 этаже.

8.В квадрат с вершинами O(0,0),K(0,2),L(2,2),M(2,0)

наудачу ставится точка P(x,y). Найти вероятность того, что координаты этой точки удовлетворяют неравенству

>2 .

9.На отрезок OB длины 30 см наудачу ставится точка. Найти вероятность того, что расстояние от этой точки до любого конца отрезка больше 10 см.

Практикум №2 « Случайные события. Классическое определение вероятности. Геометрическая вероятность»