
Практикум 41
.pdf
1
Дистанционный курс « Теория вероятностей» Практикум №4 « Случайные величины»
Задача 1. В группе из 10 изделий имеется одно бракованное. Чтобы его обнаружить, наудачу берут одно изделие за другим и каждое проверяют. Построить ряд распределения, найти математическое ожидание и дисперсию числа проверенных изделий. Решение. Пусть случайная величина ξ – число проверенных изделий. Она может принимать значения 1,2,…, 10. Найдем вероятности, с которыми эти значения принимаются. Если случайная величина ξ приняла значение 1, это значит, что первое проверенное изделие оказалось бракованным. Так как бракованное изделие одно, небракованных изделий 9, а всего изделий 10, то p =
= P(ξ = 1) = . Если случайная величина ξ приняла значение 2,
то значит первое проверенное изделие было небракованным, а
второе бракованным, тогда |
|
|
|
|
|
|
|
|
|
|
|
и так да- |
||||||
|
|
|
|
|
∙ = |
|
|
|||||||||||
лее, получим следующий |
ряд распределения: |
|
|
|
|
|||||||||||||
|
p |
= P(ξ = 2) = |
|
|
|
|
||||||||||||
|
1 |
2 |
3 |
|
4 |
|
5 |
6 |
7 |
|
8 |
|
9 |
10 |
||||
|
1 |
1 |
1 |
|
1 |
|
1 |
1 |
1 |
|
1 |
|
1 |
1 |
||||
|
10 |
10 |
10 |
10 |
|
10 |
10 |
10 |
|
|
10 |
|
|
10 |
10 |
|||
Найдем математическое ожидание данной случайной величины
по формуле: M[ξ] = ∑ |
x p , получим: |
|
. |
||||||||||||||||||
M[ξ] = 1∙ |
|
|
|
+2∙ |
|
|
+ +10∙ |
|
|
= |
|
|
|
(1+ +10) = 5,5 |
|||||||
|
|
|
|
|
|
|
|||||||||||||||
Теперь вычислим дисперсию по формуле: |
D[ξ] = M[ξ ]− M [ξ] |
||||||||||||||||||||
D[ξ] = 1 |
∙ |
1 |
+2 |
∙ |
1 |
+ +10 |
∙ |
1 |
−(5,5) = |
|
|||||||||||
1 |
|
10 |
|
10 |
|
|
|
101 |
|
10∙11∙21 |
|
||||||||||
= |
10 |
(1 +2 |
+ +10 )− (5,5) |
= |
10 |
∙ |
6 |
−(5,5) = |
|||||||||||||
Практикум №4 «Случайные величины»

|
77 |
|
11 |
|
77 |
|
121 |
|
2 |
|
33 |
|
= |
− |
= |
− |
= |
154 −121 |
= |
= 8,25 |
|||||
2 |
2 |
2 |
4 |
4 |
4 |
Задача 2. В урне 3белых и 5 черных шаров. Наудачу извлекают три шара. Пусть ξ – число вынутых черных шаров. Построить ряд распределения случайной величины ξ, найти функцию распределения, построить ее график и найти математическое ожидание.
Решение. Данная случайная величина может принимать значения 0,1,2,3. Вероятности, с которыми эти значения принимаются, вычислим, используя классическое определение вероятности и формулы комбинаторики:
|
p = P(ξ = 0) |
= |
|
C |
∙C |
|
= |
|
|
1 |
= |
|
|
|
3!5! |
|
|
= |
|
2∙3 |
= |
1 |
|
|
||||||||
|
|
|
|
|
|
|
|
8! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
C |
|
|
5!∙6∙7∙8 |
6∙7∙8 |
56 |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
3!5! |
|
|
|
|
|
||||||||||||||
p = P(ξ = 1) = |
C |
∙C |
= |
|
|
|
3!5!3!5! |
|
= |
2!∙3∙4!∙5∙3!∙5! |
= |
|||||||||||||||||||||
|
|
3∙5 |
15 |
|
|
|
|
C |
|
|
2!1!1!4!8! |
|
2!∙4!∙5!∙6∙7∙8 |
|||||||||||||||||||
= |
|
7∙8 |
= |
56 |
C ∙C |
|
|
3!5!3!5! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
p |
|
= P(ξ = 2) = |
|
|
C |
= |
1!2!2!3!8! |
= |
30 |
|
|
15 |
|
|
|
|
|
|
|
|||||||||||||
|
|
2!∙3∙2!∙3∙4∙5∙3!∙5! |
|
|
|
3∙3∙4∙5 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
= |
|
2!∙2!∙3!∙5!∙6∙7∙8 |
|
= |
6∙7∙8 |
|
= |
56 |
= |
28 |
|
|
5 |
|
|
|||||||||||||||||
|
|
p = P(ξ = 3) = |
C ∙C |
|
= |
|
5!3!5! |
= |
2!∙3∙4∙5∙3!∙5! |
= |
|
|
||||||||||||||||||||
|
|
|
C |
|
|
3!2!8! |
|
3!∙2!∙5!∙6∙7∙8 |
28 |
|
|
|||||||||||||||||||||
Таким образом, ряд распределения случайной величины ξ будет иметь следующий вид:
|
|
0 |
|
1 |
|
2 |
|
3 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Практикум №4 «Случайные величины»
3
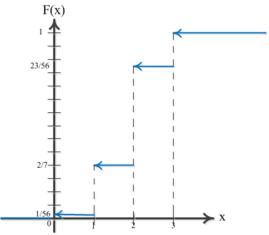
Найдем функцию распределения данной случайной величины:
1.Если x ≤ 0, то F(x) = 0;
2.если 0 < x ≤ 1 , то
1 F(x) = ( = 0) = 56
3. если 1 < x ≤ 2, то
1 F(x) = P(ξ = 0) +P(ξ = 1) = 56 +
+ |
15 |
= |
16 |
= |
2 |
56 |
56 |
7 |
4.если 2 < x ≤ 3, то
F(x) = P(ξ = 0)+P(ξ = 1) +
1 15 15 23 +P(ξ = 2) = 56 +56 +28 = 28
5. если x > 3, то
F(x) = P(ξ = 0) +P(ξ = 1)+P(ξ = 2) +
+P(ξ = 3) = |
1 |
+ |
15 |
+ |
15 |
+ |
5 |
= 1 |
|
56 |
56 |
28 |
28 |
||||||
Получаем: |
|
1 |
|
0, |
≤ 0 |
|
|
||
|
|
|
|
||||||
|
|
56 |
,0 < |
≤ 1 |
|
||||
|
|
2 |
|
|
|
|
|
|
|
( ) = |
7 |
,1 < |
≤ 2 |
|
|
||||
|
23 |
,2 < |
≤ 3 |
|
|||||
|
|
28 |
|
||||||
|
1, |
|
> 3 |
|
|
||||
Построим график данной функции:
Практикум №4 «Случайные величины»
4
Рис.1
Вычислим математическое ожидание случайной величины ξ:
M[ξ] = 0∙1/56+1∙15/56+2∙15/28+3∙5/28=15/56+30/28+15/28=15/8.
Задача 3. Найти закон распределения дискретной случайной величины ξ, которая может принимать только два значения: x1 – с вероятностью p1 = 0,4 и x2 (причем x1<x2) , если известны математическое ожидание M[ξ] = 3,2 и дисперсия D[ξ] = 0,96.
Решение. Так как p1 + p2 = 1, то p2 = 1 - p1 = 1 - 0,4 = 0,6.
Математическое ожидание вычисляется по формуле: M[ξ] = x1p1+x2p2 , а дисперсия: D[ξ] = M[ξ2] - M2[ξ] = x12p1 +
+ x22p2 - M2[ξ] . Используя условия задачи, получим систему двух уравнений:
Умножим каждое уравнение на 5, получим:
Практикум №4 «Случайные величины»
|
|
|
|
|
2x |
|
|
5 |
= 16 |
|
|
|
||||
|
|
|
|
|
|
+3x |
|
|
|
|||||||
Решаем эту систему |
методом подстановки, то есть |
|||||||||||||||
|
2x |
|
+3x |
= 56 |
|
|
|
|||||||||
|
|
|
|
|
|
x |
= |
16 − 3x |
|
|
|
|
||||
|
|
|
|
|
16 −3x |
2 |
|
|
|
|
||||||
оно имеет корниx |
2 |
|
|
|
|
|
|
|
+3x = 56 |
|||||||
|
2 |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
, тогда5x |
− 32x +48 = 0. |
||||||||
Для переменной |
получаем уравнение: |
, |
||||||||||||||
Но так как по |
|
|
x , |
= 4, x , |
|
,=то |
|
x , |
= 2,. Теперьx , =со- |
|||||||
|
условию |
:< x |
|
|
|
x = 2, x |
= 4 |
|
||||||||
ставим ряд распределенияx |
|
|
|
|
||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
0,4 |
|
|
|
|
|
|
0,6 |
|
|
|
||
Задача 4. Случайная величина ξ задана функцией распределе-
ния: |
x |
|
0,x ≤ 0 |
F(x) = |
|
||
|
,0 < x ≤ 3 |
||
|
3 |
1,x > 3 |
|
Найти плотность распределения вероятностей ( ( )) и вероятность того, что в результате испытания случайная величина примет значение из интервала (2,3).
Решение. Так как f(x) = F (x), то
( ) |
1 |
0, |
x ≤ 0 |
f x = |
3 |
, |
0 < x ≤ 3 |
|
0, |
x > 3 |
|
Вероятность попадания случайной величины на указанный интервал вычисляем по формуле: P(α < ξ < β) = F(β)− F(α).
Тогда P(2 < ξ < 3) = F(3)− F(2) = − = .
Практикум №4 «Случайные величины»

6
Задача 5. Закон распределения случайной величины ξ задан с
помощью плотности распределения вероятностей:
a f(x) = 1+x
Найти коэффициент , функцию распределения, вероятность
того, что случайная величина примет значение, большее .
Решение. 1. Коэффициент |
найдем, воспользовавшись |
следу- |
|||||||||||||||||||||||||
√3 |
|||||||||||||||||||||||||||
ющим свойством плотности распределения: |
∫ f x dx = 1 |
||||||||||||||||||||||||||
ем |
∫ |
|
|
dx = a∙arctgx| |
|
|
= a |
|
|
− − |
|
|
= a∙π |
|
|
||||||||||||
гда |
|
|
|
|
|
a∙π = 1 a = |
|
|
|
|
|
|
|
|
|
|
|
|
( ) |
, получа- |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
2.Теперь |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
равенство |
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
найдем функцию распределения по формуле: |
|
||||||||||||||||||||||
F(x) = ∫ |
f(t)dt, получаем F(x) = |
|
|
|
∫ |
|
|
|
dt = |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||
1 |
|
|
|
|
|
1 |
|
|
|
|
π |
1 |
|
|
|
1 |
|
|
|||||||||
= |
π |
arctgt| |
|
|
= |
π |
arctgx− |
|
− |
2 |
|
= |
π |
arctgx+ |
2 |
|
|
||||||||||
3. Вычислим вероятность того, что случайная величина примет
значение, большее √3 . Для этого воспользуемся формулой:
P(α < ξ < β) = ∫ f(x)dx, получаем
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
P ξ > √3 = |
|
|
|
|
|
|
dx == |
arctgx|√ |
|
|
|
|
|
|
|||||||||||
π |
√ |
|
|
|
1+x |
π |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
1 |
|
|
π |
|
|
|
|
|
|
1 |
π |
|
π |
|
1 |
|
π |
|
1 |
|
|
|
|
|
= |
|
|
−arctg√3 |
= |
− |
= |
∙ |
= |
|||||||||||||
|
|
|
|
π |
|
|
2 |
π |
2 |
3 |
π |
6 |
6 |
||||||||||||
Задача 6. Найти математическое ожидание случайной величины
η=2ξ+7, если M[ξ] = 4.
Решение. Воспользуемся свойствами математического ожида-
ния: M[η] = M[2ξ+7] = 2M[ξ]+M[7] = 2∙4+7 = 15.
Задача 7. Случайная величина ξ имеет равномерное распределение с математическим ожиданием M[ξ] = 1 и дисперсией
Практикум №4 «Случайные величины»

7
D[ξ] = 3. Найти плотность распределения вероятностей данной случайной величины.
Решение. Так как случайная величина имеет равномерное рас-
задачи, |
|
|
|
M[ξ] = |
|
|
|
, |
|
D[ξ] = |
( |
) |
|
|
|
|||||||
пределение, то |
|
|
|
|
|
|
|
|
a+b |
. |
Используя условия |
|||||||||||
|
составим систему: |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
= 1 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
(b −a) |
|
|
|
|
|
|
||||||
Решаем систему методом |
подстановки: выражаем из первого |
|||||||||||||||||||||
|
|
12 |
|
|
= 3 |
|
|
|
||||||||||||||
уравнения a и подставляем во второе уравнение, получаем: |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
a = 2 −b |
|
|
|||||||||
|
|
|
|
, тогда |
|
|
(2b− 2) |
|
= 36 |
|
. |
|||||||||||
Решаем второе уравнение(b:−2+b) |
|
= 36 |
, получаем |
|||||||||||||||||||
b = 4, b |
= −2 |
|
|
|
a |
= 2 −4 = −2, a |
= 2 −(−2) = 4 |
|||||||||||||||
Так как |
a < b |
|
|
a = −2,b = 4 |
|
|
|
|
|
|
|
|||||||||||
|
, то |
|
|
|
|
|
|
|
|
|
|
. Тогда плотность распределения |
||||||||||
вероятностей будет иметь вид: |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
f(x) = |
0, |
( |
|
|
) |
, x [−2;4] |
или |
||||||||||||
|
|
|
|
|
|
|
|
|
|
x [−2;4] |
|
|||||||||||
|
|
|
|
f(x) = |
|
0 |
|
|
, |
x [−2;4] |
|
|||||||||||
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
, |
x [−2;4] |
|
|||||||||||||||
Задача 8. Автобусы некоторого маршрута идут строго по расписанию. Интервал движения 8 минут. Найти вероятность того, что пассажир, подошедший к остановке, будет ожидать очередного автобуса не менее 3 минут.
Решение. Пусть ξ – время ожидания пассажиром автобуса, данная случайная величина имеет равномерное распределение на отрезке [0;8], тогда плотность распределения имеет вид:
Практикум №4 «Случайные величины»

|
1 |
|
8 |
|
|
|
|
|
|
|
|
|
|
, x [0;8] |
|
|
|
|
|||||
f(x) = |
8 |
|
|
|
|
|
|||||
По условию задачи надо |
0, |
x [0;8] |
|
, эту вероятность |
|||||||
чаем: |
найти |
P(α ≤ ξ ≤ β) |
|||||||||
|
|
|
= ∫ f(x)dx |
||||||||
можно вычислить по формуле: |
P(3 ≤ ξ ≤ 8) |
|
|
, полу- |
|||||||
|
1 |
|
|
1 |
1 |
|
5 |
||||
P(3 ≤ ξ ≤ 8) = |
8 |
dx = |
8 |
x| = |
8 |
(8− 3) = |
8 |
|
|||
Задача 9. Непрерывная случайная величина ξ распределена по показательному закону:
f(x) = |
0, |
x < 0 |
2e , |
x ≥ 0 |
Найти вероятность попадания данной случайной величины на интервал (0,1;0,7).
Решение. Искомую вероятность вычисляем по формуле:
Получаем: |
P(α < ξ < β) = |
f(x)dx |
, |
|
|||
P(0,1 < ξ < 0,7) = |
|
, |
|
1 |
|
|
|
, |
2e dx = 2 |
− |
2 |
e |
| , |
= . |
|
= −(e , − e , ) ≈ 0,8187 − 0,2466 = 0,5721 ≈ 0,57
Задача 10. График плотности распределения вероятностей случайной величины ξ изображен на рис.2. Найти α, записать аналитическое выражение для плотности, найти математическое ожидание и дисперсию данной случайной величины.
Практикум №4 «Случайные величины»
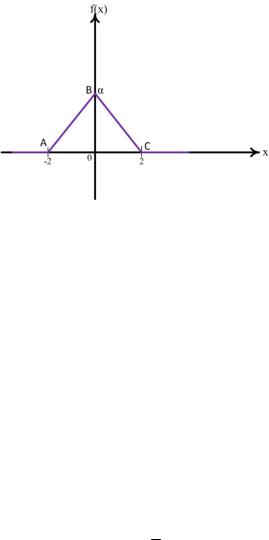
9
Рис.2
Решение. Параметр α можно найти, используя следующее свойство плотности распределения: площадь под кривой распределения равна 1, то есть площадь треугольника ABC должна равняться 1. Площадь треугольника можно найти по формуле:
S = 1/2∙a∙ha , так как a = AC = 4, ha = BO = α , тогда 1/2∙4∙α = 1,
отсюда α = 1/2.
Чтобы записать аналитическое выражения для плотности распределения, надо составить уравнения прямых AB и BC , воспользуемся уравнением y = kx+b, подставим в него сначала координаты точек A и B, получим систему:
2k b
y 1b 2
Практикум №4 «Случайные величины»

10
Решив эту систему, получим уравнение прямой AB: y =1/4x+1/2. Аналогично для второй прямой, подставим координаты точек B и C, получим систему:
2k+b = 0
|
|
1 |
|
|
||
Решив данную систему, |
получим уравнение прямой BC: |
|||||
b = 2 |
1 |
|||||
|
1 |
|
|
|
||
|
y = − |
4 |
x+ |
2 |
||
Теперь можно записать аналитическое выражение для плотности распределения:
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
0, |
|
x ≤ −2 |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
4 |
x+ |
2 |
, |
|
|
|
−2 < x ≤ 0 |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
f(x) = |
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
− |
|
|
x+ |
|
|
|
|
, |
|
|
|
|
|
0 < x ≤ 2 |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Математическое |
ожидание4 случайной2 |
величины находим по |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
0, |
|
|
|
x > 2 |
|
|
|
|
|
|
|
||||||||||||||||||
формуле: M[ξ] = ∫ |
xf(x)dx, получаем: |
|
f(x)dx = |
|||||||||||||||||||||||||||||||||||
M[ξ] = |
|
|
f(x)dx+ |
|
|
|
|
|
f(x)dx+ |
|
|
f(x)dx+ |
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
1 |
|
|
|
||||||||||
= |
|
|
x∙0∙dx+ |
|
|
x |
4 |
x+ |
2 |
dx+ |
|
x − |
4 |
x+ |
2 |
|
dx+ |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|||||||
+ |
|
|
x∙0∙dx = |
|
|
4 |
x |
+ |
|
2 |
x dx+ |
|
− |
4 |
x |
+ |
2 |
x |
dx = |
|||||||||||||||||||
1 |
|
x |
1 |
|
x |
|
|
|
|
|
|
|
|
1 |
|
x |
|
1 |
x |
|
−8 |
|
4 |
|||||||||||||||
= |
4 |
∙ |
3 |
+ |
2 |
∙ |
|
2 |
| + − |
4 |
|
∙ |
3 |
+ |
2 |
∙ |
2 |
| = − |
|
12 |
|
+ |
4 |
+ |
||||||||||||||
84
+−12 + 4 = 0
Данный ответ можно было получить сразу, глядя на график плотности распределения, он симметричен относительно оси
Практикум №4 «Случайные величины»
