мат_модели_logistics

Если суммарный запас груза совпадает с суммарным спросом, то

есть

то задачу называют закрытой, в противном случае – открытой. Составим математическую модель задачи. Обозначим через xij

количество груза, планируемое к перевозке из i-го пункта поставки в j-ый пункт потребления. Через t – время наиболее продолжительной

перевозки. Оптимальным будет план (x11, x12 ,..., xmn ) , самая продол-

жительная перевозка которого минимизируется. Модель закрытой

задачи имеет вид

Как видно, целевая функция является нелинейной. Обратные пе- ревозки не предполагаются.

Решаем задачу сведением ее к задаче о максимальном потоке. Для этого строится сеть с m+n+2 вершинами, из которых m вер-

шин соответствуют поставщикам Ai, а n – потребителям Bj, две ос- тавшиеся соответствуют истоку I и стоку S.

Пропускные способности ребер полагают равными:

доставки по ребрам (I, Ai ) и (Bj ,S ) считаются равными нулю: tIAi = tBj S = 0 . Граф транспортной сети приведен на рис. 6.7.

110

Р и с. 6.7. Граф транспортной сети

После построения сети отыскивается поток заданной мощности:

при котором maxtij достигает минимальной величины. В процессе

этого поиска при наличии альтернативы исключаются из рассмотре- ния маршруты с более продолжительными поставками. Решение за- канчивается, когда замена более продолжительных маршрутов менее продолжительными невозможна.

Другими приложениями задачи о максимальном потоке являют-

ся:

–задача определения максимальной пропускной способности трубопровода для транспортировки груза угольной пульпы от уголь- ных шахт к электростанциям;

–определение максимальной пропускной способности (макси- мального потока) сети трубопроводов для транспортировки сырой

нефти от буровых скважин до нефтеперегонных заводов и целый ряд других задач.

ЛЕКЦИЯ 13

6.8. Задача нахождения кратчайшего пути

Задача состоит в нахождении связанных между собой дорог на транспортной сети, которые в совокупности имеют минимальную длину от исходного пункта до пункта назначения.

Введем обозначения: dij – расстояние на сети между смежными

111

ла j можно вычислить лишь после того, как определено кратчайшее расстояние до каждого предыдущего узла, соединенного дугой с уз- лом j . Процедура завершается, когда получено uj последнего звена.

Пример. Рассмотрим граф, представленный на рис. 6.8.

Р и с. 6.8

Определить кратчайшее расстояние между узлами 1 и 7. Решение. Найдем минимальные расстояния:

u1 = 0 ,

u3 = u1 + d12 = 0 + 2 = 2 , u3 = u1 + d13 = 0 + 4 = 4 ,

u4 = min{u1 + d14 ;u2 + d24 ;u3 + d34} = min{0 +10;2 +11;4 + 3} = 7 , u5 = min{u2 + d25 ;u4 + d45 } = min{2 + 5;7 + 8} = 7 ,

u6 = min{u3 + d36 ;u4 + d46 } = min{4 +1;7 + 7} = 5 ,

u7 = min{u5 + d56 ;u6 + d67 } = min{7 + 6;5 + 9} =13 .

Минимальное расстояние между узлами 1 и 7 равно 13, а соот-

112

ветствующий маршрут содержит узлы 1–2–5–7.

К такой задаче сводится целый ряд задач, таких как:

–задача о замене оборудования;

–построение критического пути в сетевых графиках;

–построение сетей максимальной надежности;

–рациональное размещение пунктов обслуживания и т.д. Существует ряд алгоритмов нахождения кратчайшего пути. Из

них самыми известными являются:

–алгоритм Дейкстры;

–алгоритм Флойда;

–алгоритм Форда-Фалкерсона.

Алгоритм Дейкстры разработан для нахождения кратчайшего пути между заданным исходным узлом и любым другим узлом сети.

Алгоритм Флойда более общий, поскольку он позволяет одно-

временно найти минимальные пути между любыми двумя узлами сети.

6.9. Решение задачи методом Форда-Фалкерсона

Остановимся подробнее на алгоритме Форда-Фалкерсона.

Алгоритм может быть использован для нахождения кратчайших путей на графах, если вести поиск от некоторой вершины до всех остальных вершин. Алгоритм относится к числу итерационных.

При расчете графов на ЭВМ информацию о графе удобно хра- нить в матричном виде. Граф обычно задается с указанием длин дуг, поэтому записывается матрица весов дуг. Такая матрица квадратная с числом строк (столбцов), равным числу вершин графа. На пересе- чении i-ой строки и j-го столбца в ней ставится:

– 0, если i = j (либо это отсутствующая петля, либо длина дуги равна 0);

– l , если имеется связь u (i, j) из вершины i в вершину j , где l – длина дуги из i в j ;

– ∞ , если нет связи из i в j .

При практической реализации на ЭВМ вместо ∞ можно исполь- зовать достаточно большое число.

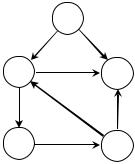
В качестве примера рассмотрим граф, изображенный на рис. 6.9.

113

6.10. Нахождение общей медианы графа

Обозначим через q – числовую характеристику – вес вершин графа.

114

Пусть граф является, например, моделью процесса транспорти- ровки деталей между станками механического участка. Тогда под весами вершин можно понимать производительность станка (число обработанных деталей в ед. времени) или пропускную способность железнодорожного узла.

Внешним передаточным числом W1 вершины с номером 1 графа

где k – число вершин графа, Cmin (1, j) – элементы 1-ой строки мат- рицы кратчайших путей [Cmin ] .

Если внешние передаточные числа всех вершин графа записать в виде вектор-столбца [W ] , а веса вершин в виде вектор-столбца [q] ,

Внутренней медианой графа называется вершина, для которой внутреннее передаточное число минимально.

Если сложить два вектора [W ] и [t] , получим новый вектор:

на номер вершины, которую называют общей медианой графа G . Таким образом, общая медиана графа характеризуется мини-

мальной суммой внутреннего и внешнего передаточных чисел. Пример. В цехе имеются 5 участков, объединенных в сеть по-

средством транспортных связей. Каждый участок производит неко-

115

торую продукцию и нуждается в обслуживании (настройке) инстру- ментом. Инструмент доставляется на участок настройки немедленно после обнаружения погрешности. Сведения об относительной произ-

водительности участков [q] и расстояниях между ними даны на гра-

фе (рис. 6.10). Где следует выбрать место для участка настройки, чтобы временные затраты на транспортировку были минимальными?

Р и с. 6.10

Требуется выбрать из 5 участков один, для которого транспор- тировка от него и обратно наиболее выгодна. Относительная потреб- ность в настройке будет считаться пропорциональной производи- тельности.

Матрица весов дуг графа – модели механического цеха, имеет

вид:

матрица весов вершин –

116

свойством будет обладать участок 4 (рис. 6.10), которому в модели на графе соответствует общая медиана.

6.11. Расчет надежности сетей

При решении этой задачи на графе каждой дуге ставится в соот- ветствие надежность перемещения груза по дуге сети (т.е. вероят- ность безотказной работы).

Рассмотрим пример. Исследуется система перемещения груза по

117

городским улицам. Служба движения располагает статистическими

данными о вероятности безаварийного проезда автотранспорта по той или иной улице в том или ином направлении.

Задача моделируется графом (рис. 6.11), вершины которого – перекрестки (или характерные объекты, с помощью которых можно описать путь перемещения грузов).

Р и с. 6.11

Веса дуг – вероятности безаварийного проезда.

Требуется определить вероятности безаварийного проезда по тому или иному пути, т.е.вероятность безопасного перемещения по пути (см. рис. 6.11), которая определяется произведением вероятно-

стей

Учитывая, что нас интересует максимально безопасный путь, потребуем, чтобы Ps = max .

С учетом того, что вероятности безопасного проезда находятся в интервале от 0 до 1, ln(Pi ) < 0 .

Путь с вероятностью безопасного проезда близкой к 1 имеет от- рицательный, близкий к 0, логарифм.

Наоборот, если путь отличается малой вероятностью безаварий- ного проезда, логарифм его отрицателен и близок к бесконечности. Если же все значения логарифмов вероятностей безаварийного про- езда умножить на (–1), тогда путь с малой вероятностью безаварий-

ного проезда будет иметь очень большую положительную величину (на графе – ∞ ), а путь с высокой вероятностью безаварийности бу- дет характеризоваться малой положительной величиной.

Следовательно, для поиска пути с максимальной безаварийно- стью можно применить алгоритм поиска кратчайшего пути на задан- ном графе.

Дуги такого графа будут характеризоваться логарифмами веро- ятностей безотказного проезда, умноженными на (–1).

Проиллюстрируем вышеизложенное.

118