ДС Радиооптика_1 / Литература ч.1 / Введение в радиооптику

Г.Г. Червяков, В.В. Роздобудько

УДК 621.396.6(075) ББК 32.86 Ч-45

Рецензенты: П. В. Серба, д-р физ.-мат. наук, профессор. В. К. Лебедев, канд. техн. наук, ст. науч. сотр.

ная литература», 2009. − 260с.

Пособие предназначено для изучения курса «Оптические устройства радиотехники» студентами радиотехнических специальностей.

Излагаются вопросы необходимые для понимания методов и средств решения основных задач радиотехники оптическими приемами. Приводится детальный анализ наиболее часто встречающихся радиооптических систем, даются конкретные примеры проникновения методов радиотехники в оптический диапазон, с одной стороны, и внедрение оптических методов и устройств в радиотехнику − с другой.

Поскольку спектр радиооптических технологий гораздо шире, то в пособие включены достаточно полные сведения об оптическом волокне, волоконно-оптических элементах, системах и устройствах оптического диапазона с рассмотрением физических процессов в них и анализом параметров, приводятся методики расчета систем связи на их основе.

Табл. 33. Ил. 144. Библиогр.: 108 назв.

ББК 32.86 Ч-45

© Червяков Г.Г., Роздобудько В.В., 2009

2

Введение в радиооптику

1.5.Дифракционная формула в приближениях Френеля и Фра-

унгофера…………………………………………………………….. 15

1.6.Импульсный отклик и передаточная функция слоя про-

странства…………………………………………………………….. 18

2. Когерентные оптические процессоры……………………….. 25

2.1.Пространственное преобразование Фурье в ОС……………... 25

2.2Оптический спектроанализатор……………………………….. 31

2.3.Принцип пространственной фильтрации…………………….. 35

2.4.Оптический коррелятор……………………………………….. 37

2.5.Акустооптические модуляторы………………………………. 39

2.6.Оптические модуляторы………………………………………. 46

2.7.Базовые элементы акустооптических процессоров………….. 58

4.2.Акустооптические анализаторы спектра с временным ин-

тегрированием………………………………………………………. 110

4.3.Aкустический процессор обработки сигналов фазированных антенных решеток…………………………………………………... 113

5. Антенные решетки с многоканальными акустооптичеки-

ми модуляторами………………………………………………….. 118

5.1. Структурная схема радиооптической антенной решетки…… 119 5.2. Радиооптическая антенная решетка с функциями пеленгато-

ра-частотомера……………………………………………………… 120

3

Г.Г. Червяков, В.В. Роздобудько

7.1.Линейная часть фотоприемного тракта………………………. 179

7.2.Особенности построения аналоговых и цифровых систем

9.1.Оценка величины усилительного участка ВОСС……………. 236

9.2.Выбор сигналов цифрового линейного тракта ВОСС……….. 241

4

Введение в радиооптику

ВВЕДЕНИЕ

Научное направление «Радиооптика» появилось в конце 50-х годов ХХ века вместе с первыми многообещающими результатами исследований и заняло в радиоэлектронике свое прочное место. Этому способствовали такие обстоятельства как: уникальная обработка сигналов бортовых РЛС с синтезированной апертурой для получения изображения земной поверхности с высоким угловым разрешением (впервые электронные методы обработки радиосигналов были дополнены оптическими), внедрение в оптотехнику (и в смежные научно-технические области) источников когерентного излучения − лазеров и разработка методов и устройств управления и приема такого излучения, что обеспечило элементную базу устройств оптической обработки информации (ООИ).

Инженеры по радиотехнике и электронике к использованию оптических методов были готовы, поскольку процессы оптического и радиодиапазона описываются единой системой уравнений Максвелла и неудивительно, что имеется общность между оптикой и такими радиотехническими дисциплинами, как теория сигналов, теория цепей и систем. Эта общность проявляется прежде всего в том, что преобразования светового сигнала (изображения) в оптической системе происходят по тем же законам, что и преобразования радиосигналов в электрических цепях и системах, с учетом, однако, двумерной природы оптического изображения [1 − 5].

Темпы развития оптических методов обработки информации (в том числе и радиосигналов) и реализующих их устройств (оптических процессоров) определяются преимуществами когерентного излучения как носителя информации:

−высокая информационная емкость (обусловленная как двумерной природой оптического изображения, так и высокой частотой светового носителя);

−простота двумерных пространственных интегральных преобразований над световым полем (следствие физических закономерностей распространения волнового процесса оптического диапазона);

−высокая скорость обработки информации (ограничивается лишь скоростью ее ввода-вывода по причине предельно большой скорости распространения света).

5

Г.Г. Червяков, В.В. Роздобудько

1. ОСНОВНЫЕ ПРИНЦИПЫ И МЕТОДЫ ОПТИЧЕСКОЙ ОБРАБОТКИ ИНФОРМАЦИИИ

Системы ООИ в зависимости от свойств светового носителя принято подразделять на два класса: когерентные и некогерентные. В когерентных − оптическая система (без учета фотоприемника) осуществляет линейные относительно комплексной амплитуды преобразования светового поля. В некогерентных − оптическая система (ОС) выполняет преобразования линейные относительно интенсивности светового поля. Некогерентным оптическим системам (работа которых может быть описана в терминах и понятиях геометрической оптики), присущ общий недостаток: данные на ее входе, а также реакция самой системы не могут принимать отрицательных значений (интенсивности). В этом плане когерентные оптические системы, свободные от этого ограничения, имеют более высокую функциональную гибкость. Поэтому, несмотря на то, что некогерентные оптические системы ООИ находят cвoe применение в современной технике, в литературе основное внимание уделяется когерентным ООИ [4 − 6].

1.1 Пространственное преобразование Фурье

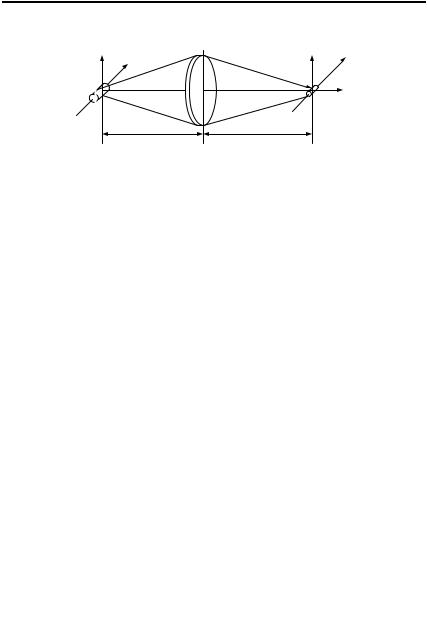
Важнейшим интегральным преобразованием, эффективно реализуемым в ОС, является пространственное преобразование Фурье [2,4]. Элементами, осуществляющими это преобразование в когерентных оптических процессорах, служат линзы. Если во входной фокальной плоскости Р1 тонкой сферической линзы (рис. 1.1) имеется распределение комплексной амплитуды светового поля u&1 (x, y) , то в выходной фокаль-

ной плоскости Р2 распределение комплексной амплитуды будет иметь вид:

S

где k = 2π/λ − волновое число; λ − длина волны света; F − фокусное расстояние линзы; S − площадь, занимаемая световым распределением в плоскости Р1.

Как видно из (1.1), в плоскости Р2 формируется пространственный комплексный спектр исходного светового распределения, а величины р = kξ/F и q = kη/F играют роль пространственных частот вдоль осей 0ξ и 0η соответственно. Цилиндрическая линза будет выполнять одномерное преобразование Фурье по одной из координат:

6

Введение в радиооптику

L

Рисунок 1.1 − Оптическая схема двумерного пространственного преобразования Фурье

При этом вторая координата остается "свободной", так что ее можно использовать, например, для организации режима многоканальной обработки светового изображения. Необходимо отметить, что формулы (1.1) и (1.2) получены в рамках скалярной теории дифракции, выводы которой справедливы для большинства задач прикладной оптики. В рамках этой теории используется скалярная величина − одна из составляющих напряженности электрического (ЭП) или магнитного поля (МП) световой волны в предположении, что другие составляющие можно рассматривать независимо таким же образом. При таком подходе полностью игнорируется тот факт, что различные компоненты векторов напряженностей ЭП и МП связаны уравнениями Максвелла и поэтому их нельзя рассматривать независимо. Эта теория является приближенной и дает правильные результаты при выполнении следующих условий:

−линейные размеры объекта, на котором дифрагирует световая волна (диафрагмы, линзы и пр.), значительно превосходят длину волны

λ;

−дифракционная картина наблюдается на расстояниях, достаточно больших по сравнению с длиной волны λ [4, 7].

Помимо этого при выводе указанных формул используются параксиальное приближение, верное для лучей, идущих под малыми углами

коптической оси, и тонкость линзы (в данном случае со смещением луча внутри тела линзы можно не считаться). Эти условия выполняются во многих практических схемах когерентных оптических процессоров. Все дальнейшее изложение ведется в рамках скалярной теории дифракции.

1.2 Основы скалярной теории дифракции

Явление дифракции (от латинского diffraction - изломанный) играет важную роль в тех разделах радиофизики, которые связаны с рас-

7

Г.Г. Червяков, В.В. Роздобудько

пространением электромагнитных (ЭМВ) волн. Степень проявления дифракционных эффектов зависит от отношения поперечных размеров препятствия к длине ЭМВ.

Как известно, проблемы дифракции ЭМВ на некотором теле сводится к определенной граничной, которая для большинства сложных объектов аналитически неразрешима. Поэтому ввиду практической важности дифракционных задач, с одной стороны, и трудностью их строгого математического разрешения − с другой, до настоящего времени разрабатываются приближенные методы решения подобных задач [2, 8]. Излагаемая здесь скалярная теория дифракции (предложена в 1882 г. Кирхгофом, а затем развита Зоммерфельдом) использует ряд приближений, из которых наиболее существенным является замена векторных функций, характеризующих амплитуды ЭМВ, скалярными функциями, представляющими собой любую составляющую либо вектора Е, либо вектора Н. Это допущение существенно упрощает основное положение теории Максвелла о взаимосвязи составляющих Е и Н (векторный характер), согласно которому в принципе невозможно рассматривать эти составляющие отдельно друг от друга.

Приближенная теория Кирхгофа-Зоммерфельда в математическом отношении достаточно проста, дает полное физическое представление о сущности дифракционного процесса и удовлетворительные для практики результаты. Условия применимости можно свести к двум требованиям:

−поперечные размеры препятствия велики по сравнению с λ;

−дифрагированное поле рассматривается в достаточном удалении от объекта дифракции.

Прежде чем изложить скалярную теорию дифракции, напомним ряд математических сведений.

Уравнение Гельмгольца. В случае линейной, однородной и изотропной среды систему уравнений Максвелла можно свести к решению волнового уравнения для произвольной временной зависимости в области, где отсутствуют источники [8].

с = (εаµа)−0,5 − скорость распространения волны; εа , µа − абсолютная диэлектрическая и магнитная проницаемости; 2 = ∂2/∂x2 + ∂2/∂y2 +∂2/∂z2 − дифракционный оператор Лапласа.

Функция U в (1.3) описывает либо электрический вектор Е, либо магнитный вектор Н поля в пространстве. В скалярной теории используют уравнение (1.3), полагая при этом, что U(x,y,z) в данном случае описывает чисто скалярную величину, а именно амплитуду волны.

8

Введение в радиооптику

ЭМП в точке Р для монохроматической волны циклической частоты ω = 2πν описывается скалярной функцией U(Р,t), которую в случае линейно поляризованных волн можно полагать совпадающей с напряженностью ЭП и МП

U(Р,t) = U(P)cos[2πνt + ϕ(P)],

где U(P) и ϕ(P) − соответственно амплитуда и фаза волны в точке Р; ν − частота.

Используя комплексные обозначения, последнее выражение перепишем в следующем виде

U(Р,t) = Re[U(P)exp(−i2πνt)],

где U(Р) = U(P)exp(−iϕ(P)), комплексная амплитуда, a Re − символ действительной части функции, заключенной в квадратных скобках.

Здесь используется запись временной зависимости в виде exp(−i2πνt), а не exp(i2πνt) (как, например, в [4, 8]) и поэтому запись фазового множителя расходящейся сферической волны имеет вид exp[i(kr − 2πνt)]. В результате широко используемые в дальнейшем операторы пространственных преобразований имеют обычный, принятый для пространственных (как, впрочем, и временных) функций вид преобразования Фурье

{g(x, y)} = G(νx ,νy ) = ∫ ∞∫g(x, y)exp[−i2π(νx x +νy y)]dxdy, (1.4)

−∞

где {g(x, y)} − символ Фурье-преобразования; G(νx,νy) = {g(x, y)} − пространственный Фурье-образ (спектр Фурье, спектральная плотность) функции g(x, y); νx, νy − пространственные частоты.

Соответственно обратное преобразование Фурье-функции G(νx,νy) обозначается как {g(x, y)} и определяется выражением

−1{G(νx ,νy )}=g(x, y) =∫ ∞∫G(νx ,νy )exp[i2π(νx x +νy y)]dνxdνy . (1.5)

−∞

Подставляя в (1.3) вместо U(Р,t) комплексное значение U(P)exp(−i2πνt), получаем, что комплексная амплитуда U(P) удовлетворяет уравнению Гельмгольца

где k = 2πν/c = 2π/λ − волновое число.

Теорема Грина. Приведем формулировку теоремы Грина, являющуюся во многих отношениях основным звеном скалярной теории дифракции [8].

Пусть U(P) и G(Р) − две произвольные комплексные функции координат (x,y,z), a S − замкнутая поверхность, ограничивающая объем V

9