ДС Радиооптика_1 / Литература ч.1 / 72

Глава 3. Общая теория направляющих систем

3.1. Классификация направляющих систем

До сих пор рассматривались электромагнитные поля и волны, существующие в неограниченном пространстве. Однако часто требуется передавать электромагнитную энергию в определенном направлении. Эта задача решается с помощью специальных технических устройств — направляющих систем, обеспечивающих распространение волн только в одном или двух координатных направлениях. Отметим, что существуют и природные направляющие системы. Примером может служить воздушное пространство между поверхностью и ионосферой Земли. Последовательно отражаясь от ионосферы и поверхности Земли, радиоволны декаметрового диапазона огибают земную поверхность, благодаря чему осуществляется радиосвязь на большие расстояния при незначительной мощности передатчиков.

Более точно электромагнитной направляющей системой

называют совокупность металлических и диэлектрических тел, осуществляющих передачу (канализацию) электромагнитной энергии в определенных направлениях с малым затуханием без излучения в окружающее пространство. Примером могут служить две параллельные идеально проводящие плоскости z = const Ясно, что электромагнитная волна (свет) может распространяться между этими плоскостями (т. е. в плоскости xOy) в любом направлении, но не может распространяться в направлении оси z.

Важный класс направляющих систем составляют линии передачи (ЛП), обеспечивающие распространение энергии только в одном направлении — вдоль своей оси. Линии передачи различаются конфигурацией и материалом тел, из которых они образованы. В зависимости от конструкции и материалов направляющие системы и ЛП разделяют на отдельные типы.

Регулярными считают ЛП, свойства которых вдоль направления распространения неизменны или меняются по периодическому закону.

72

В первом случае регулярную ЛП называют продольно-однородной, во втором — периодической. Если свойства ЛП вдоль направления распространения меняются по произвольному закону, ее считают нерегулярной (продольно-неоднородной). В настоящей книге рассматриваются, в основном, регулярные ЛП.

Если электромагнитное поле ЛП не ограничено в направлениях, перпендикулярных направлению передачи энергии, то ее называют открытой. В закрытых ЛП электромагнитное поле существует только внутри замкнутой металлической оболочки.

В соответствии с материалом тел, образующих ЛП, их делят на

металлические, диэлектрические и металлодиэлектрические.

Рис. 3.1. Некоторые типы регулярных линий передачи

Свойства линий передачи существенно зависят от связности их поперечного сечения. Если любой контур, расположенный в этом сечении, можно стянуть в точку, не пересекая границу раздела диэлектрик-металл, то ЛП называют односвязной. В противном случае ЛП многосвязна, причем степень связности равна числу различных типов контуров, которые можно выделить в ее поперечном сечении.

Проиллюстрируем приведенную классификацию примерами.

73

На рис. 3.1, а изображен прямоугольный волновод — закрытая односвязная металлическая ЛП. Как будет показано, по таким металлическим трубам различного поперечного сечения могут при определенных условиях распространяться электромагнитные волны. Коаксиальный волновод (рис. 3.1, б) — хорошо известный пример закрытой металлической двухсвязной ЛП. Круглый диэлектрический волновод (ДВ) (рис. 3.1, в) — открытая диэлектрическая односвязная ЛП, которая также может использоваться для передачи электромагнитной энергии на достаточно высоких частотах, включая оптический диапазон. На рис. 3.1, г изображена открытая двухсвязная металлодиэлектрическая ЛП, называемая микрополосковой линией передачи (МПЛ). Такие ЛП широко используются в интегральных схемах микроволнового диапазона Все перечисленные типы линий передачи продольно однородны.

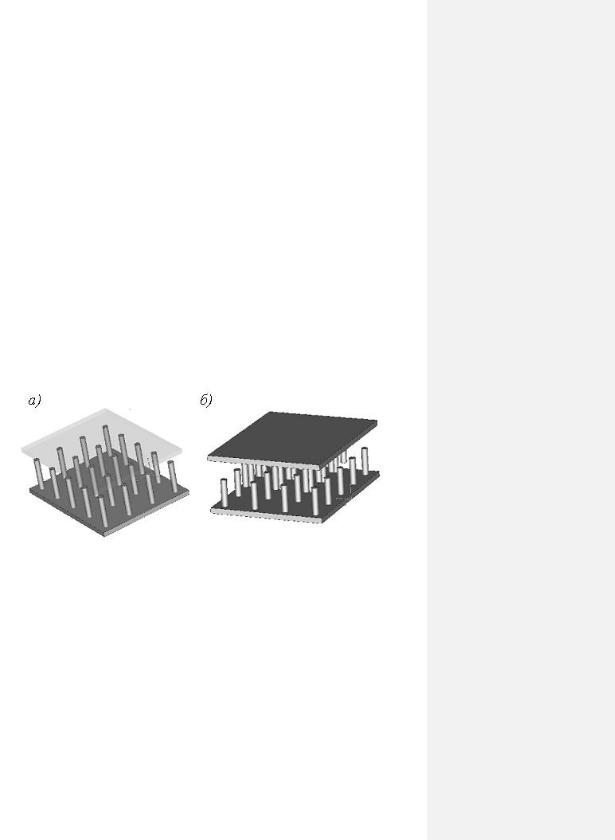
Рис. 3.2. Двухмерно периодические направдяющие системы

Гребенчатая (рис. 3.1, д) и спиральная (рис. 3.1, е) ЛП относятся к периодическим линиям передачи. В микроволновой электронике они используются для замедления электромагнитных волн. Существуют и двухмерно периодические направляющие системы, некоторые конструкции которых показаны на рис. 3.2, а (штыревая) и 3.2, б (гребенчатая).

Параметры нерегулярных ЛП могут меняться скачком (соединение двух прямоугольных волноводов с различными

74

Рис. 3.3. Нерегулярные линии передачи

поперечными размерами, рис. 3.3, а) и плавно (круглый волновод с плавным изменением радиуса трубы, рис. 3.3, б). Такую ЛП называют плавно-неоднородной.

3.2. Распространение волн между двумя параллельными

распространяющуюся между двумя параллельными идеально проводящими плоскостями Р и Q, многократно отражаясь от них под углом 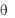(рис. 3.4). Для простоты считаем, что пространство между

75

Из записанных выражений следует, что между плоскостями в направлении оси z распространяется плоская неоднородная (так как амплитуды зависят от координаты x) волна. Ее фазовая скорость

больше скорости света. Так как в "первичной" волне, распространяющейся под углом к плоскостям P и Q, энергия переносится со скоростью света, перенос энергии вдоль оси z происходит со скоростью

vgz c sin c 1 [m /(2a)]2 . (3.5)

Как видно, эта скорость всегда меньше c. Отметим, что произведение

vpzvgz = c2.

В отличие от плоской волны в неограниченной среде, эта волна имеет продольную составляющую магнитного поля, т. е. не является поперечной. Отношение модулей поперечных составляющих поля

системы. Как видно, его величина зависит от частоты (длины волны в свободном пространстве).

Из формул (3.4) и (3.5) следует, что при = сm = 2а/т фазовая скорость обращается в бесконечность, а скорость переноса энергии — в нуль, т. е. распространение волны вдоль оси z прекращается. Поэтому

движется вдоль оси x от одной плоскости к другой, поочередно отражаясь от них. Продольная (вдоль оси z) составляющая скорости переноса энергии при этом обращается в нуль.

Распределение электромагнитного поля вдоль оси x, как это следует из формул (3.2) и (3.3), имеет вид стоячей волны. Обе плоскости P и Q расположены в узлах электрического поля, которое,

77

напомним, имеет только поперечную составляющую Ey. Вектор напряженности магнитного поля Н имеет как поперечную Нх, так и продольную Hz составляющие, причем поперечные составляющие Ёу и Нх совпадают по фазе, а продольная составляющая Hz сдвинута по отношению к ним на 90°. По мере увеличения частоты амплитуда продольной составляющей магнитного поля стремится к нулю, т. е. волна приближается к чисто поперечной. При приближении частоты к критической амплитуда поперечной составляющей магнитного поля стремится к нулю, что приводит к прекращению распространения энергии вдоль оси z.

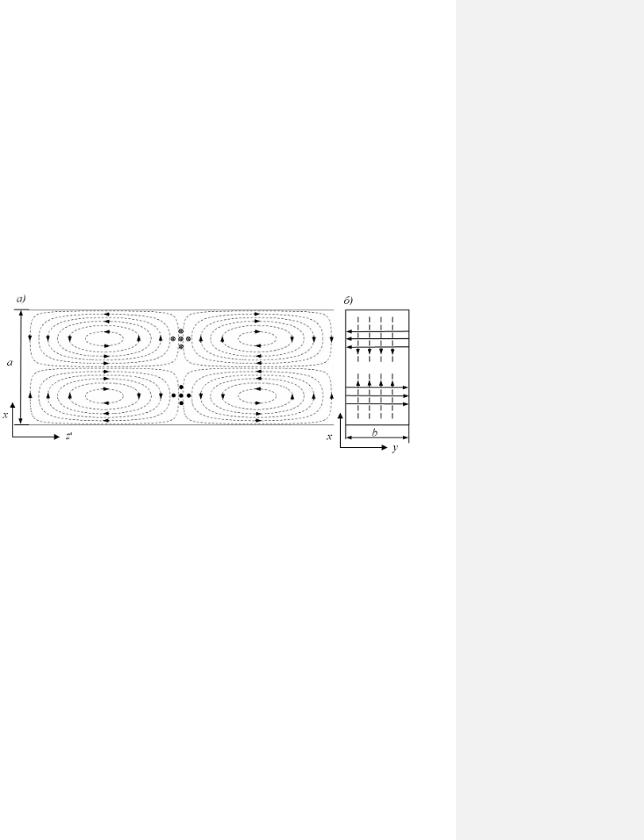
Рис. 3.5. Электрическое поле между параллельными плоскостями.

На рис. 3.5, а изображены силовые линии векторов Е и Н для т = 2 в плоскости xOz. Линии напряженности магнитного поля образуют замкнутые плоские кривые, а линии вектора Е — прямые, перпендикулярные плоскости чертежа. Если ввести еще две идеально проводящие плоскости у = const, расположенные на расстоянии b друг от друга (рис. 3.5, б), то условия распространения волны не нарушатся, так как новые плоскости перпендикулярны вектору Е и касательная составляющая напряженности электрического поля на них равна нулю.

Четыре пересекающиеся идеально проводящие плоскости образуют прямоугольный волновод (см. рис. 3.1, а). Рассмотренное поле представляет собой одно из возможных распределений поля (типов волн) в прямоугольном волноводе. Это поле можно рассматривать как суперпозицию бесконечного множества плоских

78

электромагнитных волн (парциальных волн), распространяющихся под углом к стенкам волновода. Метод анализа, основанный на таком представлении поля, называют методом (концепцией) парциальных волн. Он позволяет наглядно представить процесс распространения волн в направляющей системе и получить правильные количественные результаты. В то же время методом парциальных волн неудобно, а иногда и невозможно пользоваться в том случае, когда волновод имеет сложную форму поверхности или заполнен неоднородной и (или) анизотропной средой. Более общий подход к анализу распространения волн в линиях передачи изложен в следующих разделах.

3.3. Скалярные уравнения Гельмгольца для регулярной ЛП и их общее решение

Рассмотрим продольно однородную линию передачи, в которой отсутствуют сторонние токи и заряды. Волны, распространяющиеся в такой линии, называют свободными ( собственными). Они возбуждаются источниками, находящимися вне рассматриваемого отрезка ЛП. Анализ электромагнитного поля свободных волн целесообразно проводить с помощью векторов Герца, так это позволяет сократить число уравнений и неизвестных функций. Используем, например, электрический вектор Герца, который удовлетворяет уравнению (см. разделы 1.3, 1.6):

Это векторное уравнение эквивалентно системе трех уравнений с тремя неизвестными скалярными функциями — проекциями вектор Герца на оси координат. Отметим, что такому же уравнению удовлетворяет и магнитный вектор Герца.

Решив уравнение (3.6) с соответствующими граничными условиями, электромагнитное поле в ЛП можно вычислить с помощью формул (1.65). (1.66):

При выводе первого равенства использовано уравнение (3.6).

79

Вместо электрического можно использовать магнитный вектор Герца Γm , который также удовлетворяет уравнению (3.6). Связь этого вектора с электромагнитным полем ЛП получим из выражений (3.7), (3.8), применив свойство перестановочной двойственности уравнений электродинамики:

удовлетворяла соотношениям (3.12) и (3.13), метрические коэффициенты используемой системы координат должны быть связанными следующим соотношениям:

Системы координат, для которых выполняются условия (3.14), называют разделяющимися. К системам такого типа относится, в частности, обобщенно цилиндрическая и сферическая системы координат.

80

Если известно, что электромагнитное поле не зависит от одной из координат, например, x3 ( / x3 = 0), условия (3.14) можно ослабить. В этом случае достаточно потребовать, чтобы

В разделяющейся системе координат всегда можно подобрать функцию e, одновременно удовлетворяющую соотношениям (3.12) и (3.13).

Таким образом, любое электромагнитное поле свободных волн может быть описано с помощью двух скалярных функций — проекций вектора Γe на две координатные оси.

Изложенное справедливо и для магнитного вектора Герца Γm . Поэтому, введя функцию m, удовлетворяющую уравнениям (3.12) и (3.13), можно определить поле в ЛП с помощью двух проекций магнитного вектора Герца на оси координат. Существует, однако, еще одна возможность. Из выражений (3.7) и (3.9) следует, что векторы Герца связаны между собой соотношением

проекций электрического и магнитного векторов Герца на одно и то же направление — координатную ось x3, которую называют продольной в отличие от поперечных осей координат x1, x2. Так как в разделяющейся

одному и тому же однородному скалярному уравнению Гельмгольца

поле H-типа. Из уравнений (3.8) и (3.9) следует, что поле E-типа не

81